Abstract
标准的伪随机数值生成器不能抵挡各种加密攻击

Explanation
在对安全性要求较高的环境中，使用能够生成可预测值的函数作为随机数据源，会产生 Insecure
Randomness 错误。 电脑是一种具有确定性的机器，因此不可能产生真正的随机性。伪随机数生成器
(PRNG) 近似于随机算法，始于一个能计算后续数值的种子。 PRNG 包括两种类型：统计学的 PRNG 和密码
学的 PRNG。统计学的 PRNG 提供很多有用的统计属性，但其输出结果很容易预测，因此容易复制数值流。
在安全性所依赖的生成值不可预测的情况下，这种类型并不适用。密码学的 PRNG 生成的输出结果较难预
测， 可解决这一问题。为保证值的加密安全性，必须使攻击者根本无法、或几乎不可能鉴别生成的随机值和
真正的随机值。通常情况下，如果并未声明 PRNG 算法带有加密保护，那么它很可能就是统计学的 PRNG，
因此不应在对安全性要求较高的环境中使用，否则会导致严重的漏洞（如易于猜测的密码、可预测的加密密
钥、 Session Hijacking 和 DNS Spoofing）。 示例： 下面的代码可利用统计学的 PRNG 为购买产品后仍在有
效期内的收据创建一个 URL。
String GenerateReceiptURL(String baseUrl) {
Random ranGen = new Random();
ranGen.setSeed((new Date()).getTime());
return (baseUrl + ranGen.nextInt(400000000) + “.html”);
}
这段代码使用 Random.nextInt() 函数为它生成的收据页面生成“唯一”的标识符。由于
Random.nextInt() 是统计学的 PRNG，攻击者很容易猜到其生成的字符串。尽管收据系统的底层设计并
不完善，但若使用不会生成可预测收据标识符的随机数生成器（如密码学的 PRNG），就会更安全些

Recommendation
当不可预测性至关重要时，如大多数对安全性要求较高的环境都采用随机性，这时可以使用密码学的 PRNG
。 不管选择了哪一种 PRNG，都要始终使用带有充足熵的数值作为该算法的种子。（切勿使用诸如当前时间
之类的数值，因为它们只提供很小的熵。） Java 语言在 java.security.SecureRandom 中提供了一个加
密 PRNG。就像 java.security 中其他以算法为基础的类那样， SecureRandom 提供了与某个特定算法
集合相关的包，该包可以独立实现。当使用 SecureRandom.getInstance() 请求一个 SecureRandom
实例时，您可以申请实现某个特定的算法。如果算法可行，那么您可以将它作为 SecureRandom 的对象使
用。 如果算法不可行，或者您没有为算法明确特定的实现方法，那么会由系统为您选择 SecureRandom 的实
现方法。 Sun 在名为 SHA1PRNG 的 Java 版本中提供了一种单独实现 SecureRandom 的方式， Sun 将其描
述为计算： “SHA-1 可以计算一个真实的随机种子参数的散列值，同时，该种子参数带有一个 64 比特的计算
器， 会在每一次操作后加 1。在 160 比特的 SHA-1 输出中，只能使用 64 比特的输出 [1]。 ” 然而，文档中有
关 Sun 的 SHA1PRNG 算法实现细节的相关记录很少，人们无法了解算法实现中使用的熵的来源，因此也并不
清楚输出中到底存在多少真实的随机数值。尽管有关 Sun 的实现方法网络上有各种各样的猜测，但是有一点
无庸置疑，即算法具有很强的加密性，可以在对安全性极为敏感的各种内容中安全地使用

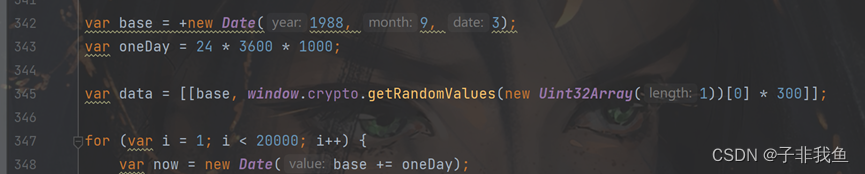
示例1：
未处理前产生的问题

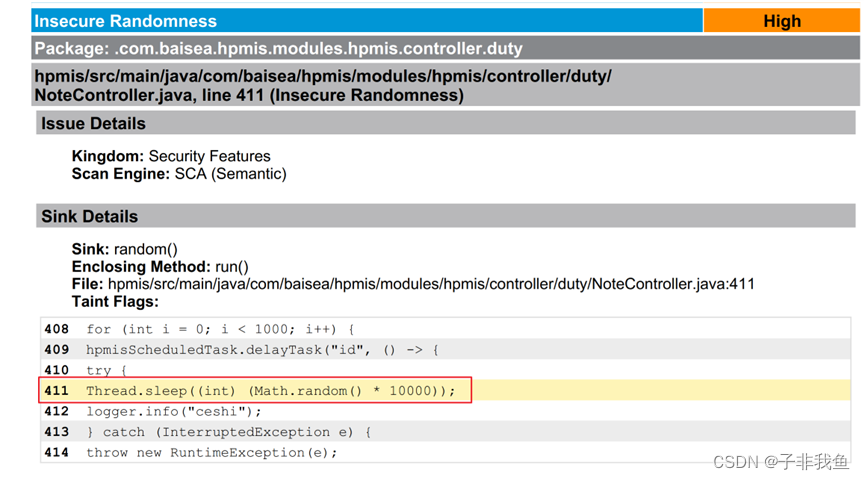
解决后如下


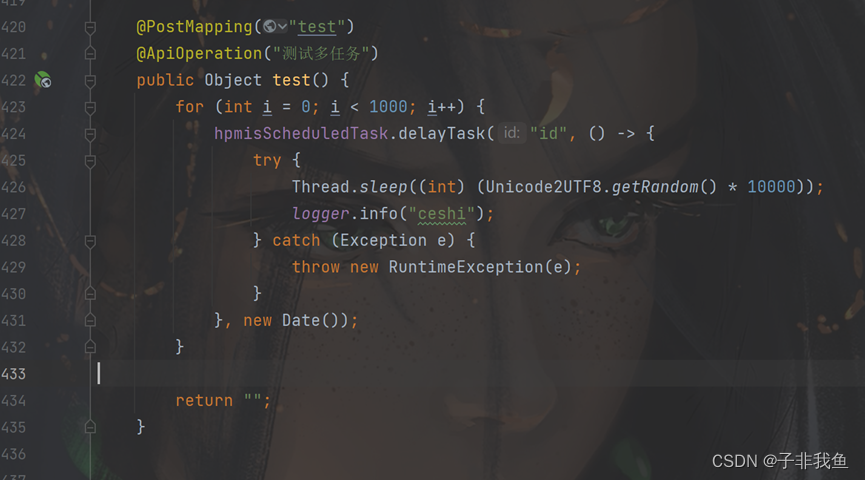
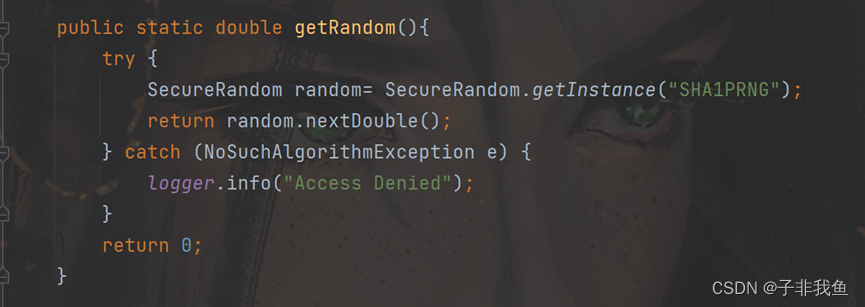
示例2，前端：
未处理前产生的问题

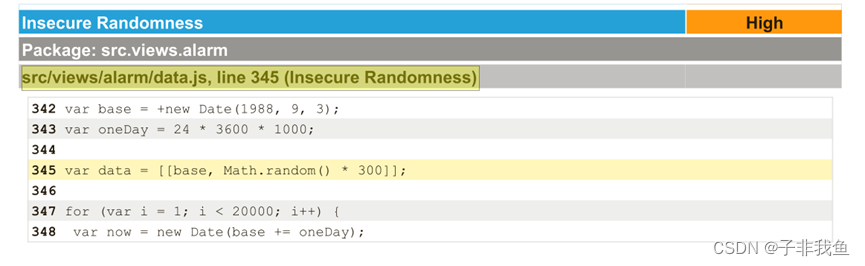
解决后如下