角点指的是窗口延任意方向移动,都有很大变化量的点。

用数学公式表示为:
这个公式表示移动后的窗口,与移动前的窗口对应元素相减的平方,为每个像素点的权重
反映了如何移动窗口,以及移动窗口后的响应值

为了让 和
直接建立关系,不用借助
,将
进行泰勒展开
最终:
假设 是互不影响的:
只有当 都不为0时
才是角点
若 相关可以通过正交化变成前面的形式
就反映了点在某个方向上的变化率,之后当
都很大时,该点才是角点

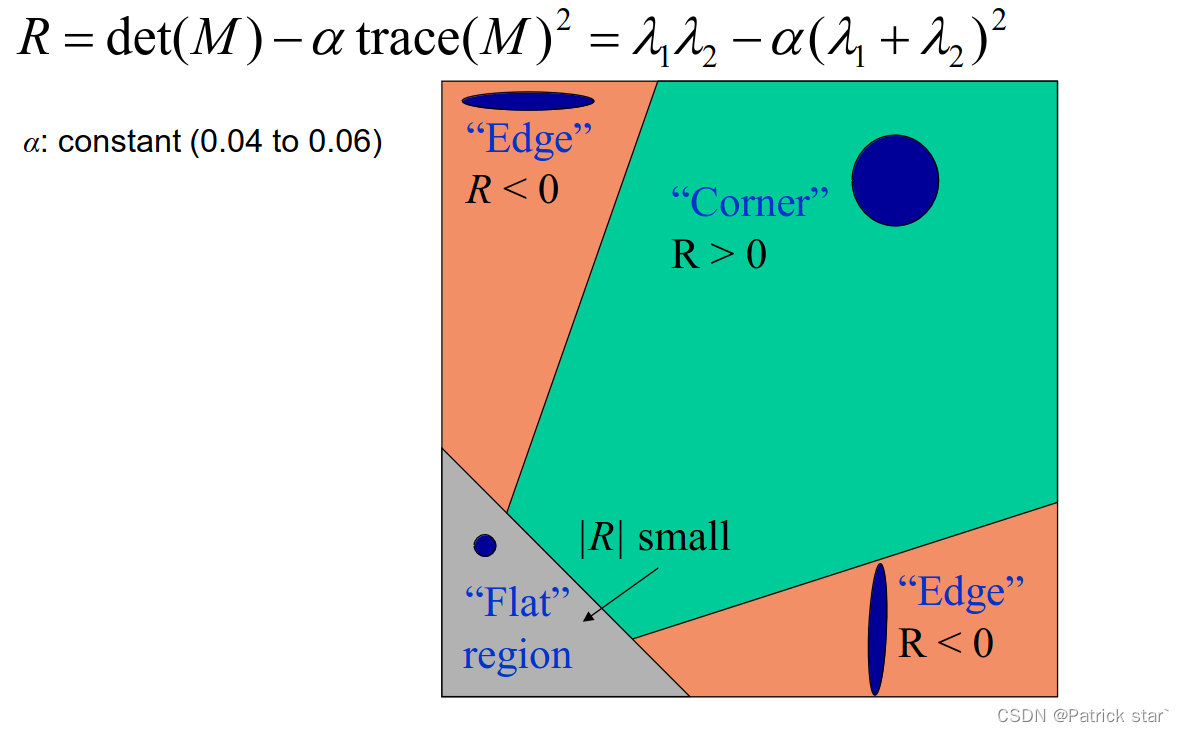
为了减少计算可以用R来判定是否为角点
角点指的是窗口延任意方向移动,都有很大变化量的点。

用数学公式表示为:
这个公式表示移动后的窗口,与移动前的窗口对应元素相减的平方,为每个像素点的权重
反映了如何移动窗口,以及移动窗口后的响应值

为了让 和
直接建立关系,不用借助
,将
进行泰勒展开
最终:
假设 是互不影响的:
只有当 都不为0时
才是角点
若 相关可以通过正交化变成前面的形式
就反映了点在某个方向上的变化率,之后当
都很大时,该点才是角点

为了减少计算可以用R来判定是否为角点

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1305896.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!