蓝桥杯省赛 数的拆分，应该是一道数论的题目
连接：数的拆分

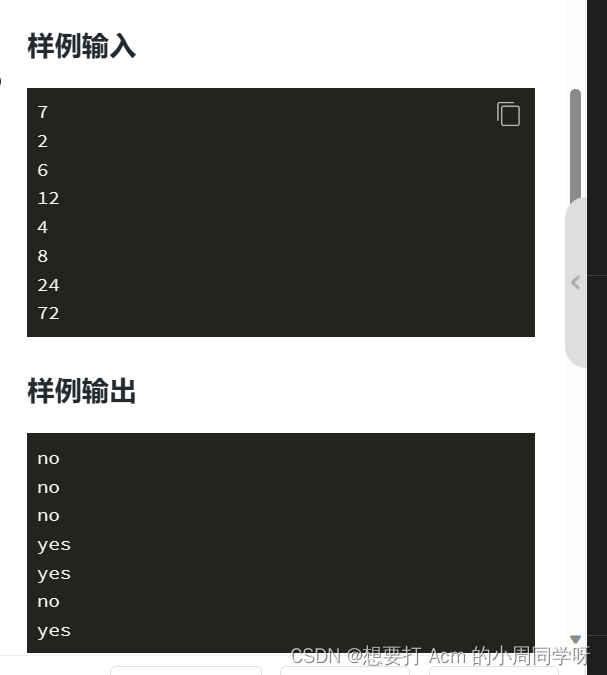
对有所有的样例，应该用long long 来表示。

n的范围是1e18次方，暴力绝对是行不通的，不能用暴力来解决。
这是一道数学的题目，需要对题目进行分析。因为要求y1 y2大于2。
关键点看出来 y1=2和y2等于3这种情况是一定符合的，所以我们对n进行质因数分解。
只要求出1e18开五次根号下面的是所有素数即可，大概400多，如果一个数字分解质因数，只出现了一次，输出no，因为此时不符合y2和y1都大于等于2的条件。当质因数分解完之后，需要判断n是否为平方数或者立方数即可，因为前面的质因数分解都是符合条件的，当一共数在n出现x次，那么肯定能拆分为2a+3b的形式，所以不管前面有多少组质因数，只要是符合条件的最后指数一定会是y1=2，y2=3的形式。

欧拉筛求质数，时间复杂度是on，速度快

void getprime()
{
  int i, j;
  for (i = 2; i <= 4500; i++)
  {
    if (!st[i])
    {
      prime.push_back(i);
    }
    for (j = 0; i * prime[j] <= 4500; j++)
    {
      st[i * prime[j]] = 1;
      if (i % prime[j] == 0)
      {
        break;
      }
    }
  }
}

求三次方的

int cbr(int x)
{
  return x * x * x;
}

校验是否为一个数字的三次方或者平方

bool check(int x)
{
  int a = (int)sqrt(x);
  if (a * a == x) // 说明是一个数字的平方
  {
    return 1; // 是整数
  }
  int y = (int)cbrt(x); // 立法跟
  if (cbr(y) == x || cbr(y + 1) == x || cbr(y - 1) == x)
  { // 数字太大有误差
    return 1;
  }
  return 0;
}

主要逻辑方法

void solve()
{
  int n;
  cin >> n;
  for (int i = 0; i < prime.size(); i++)
  {
    int x = prime[i]; // 得到对应的质数
    int cur = 0;
    if (n % x == 0)
    {
      while (n % x == 0)
      {
        n /= x;
        cur++;
      }
    }
    if (cur == 1)
    {
      cout << "no" << endl;
      return;
    }
  }
  // n已经变小了
  if (check(n))
  {
    cout << "yes" << endl;
  }
  else
  {
    cout << "no" << endl;
  }
}

main方法

signed main()
{
  // 模板而已
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);

  int t;
  t = 1;
  cin >> t;

  getprime();
  while (t--)
  {
    solve();
  }
  return 0;
}

全代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
vector<int> prime;
int st[5000];

// 线性筛保证时间是ON
void getprime()
{
  int i, j;
  for (i = 2; i <= 4500; i++)
  {
    if (!st[i])
    {
      prime.push_back(i);
    }
    for (j = 0; i * prime[j] <= 4500; j++)
    {
      st[i * prime[j]] = 1;
      if (i % prime[j] == 0)
      {
        break;
      }
    }
  }
}
int cbr(int x)
{
  return x * x * x;
}
// 检验上是否为某个数字的立方根 平方跟或者其他的
bool check(int x)
{
  int a = (int)sqrt(x);
  if (a * a == x) // 说明是一个数字的平方
  {
    return 1; // 是整数
  }
  int y = (int)cbrt(x); // 立法跟
  if (cbr(y) == x || cbr(y + 1) == x || cbr(y - 1) == x)
  { // 数字太大有误差
    return 1;
  }
  return 0;
}
void solve()
{
  int n;
  cin >> n;
  for (int i = 0; i < prime.size(); i++)
  {
    int x = prime[i]; // 得到对应的质数
    int cur = 0;
    if (n % x == 0)
    {
      while (n % x == 0)
      {
        n /= x;
        cur++;
      }
    }
    if (cur == 1)
    {
      cout << "no" << endl;
      return;
    }
  }
  // n已经变小了
  if (check(n))
  {
    cout << "yes" << endl;
  }
  else
  {
    cout << "no" << endl;
  }
}
signed main()
{
  // 模板而已
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);

  int t;
  t = 1;
  cin >> t;

  getprime();
  while (t--)
  {
    solve();
  }
  return 0;
}