class Solution:
    def rob(self, nums: List[int]) -> int:
        #dp 偷到第i个房间，最多偷了多少钱
        #dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
        if len(nums) == 1:
            return nums[0]
        if len(nums) == 2:
            return max(nums[0], nums[1])
        dp = [0] * (len(nums))
        dp[0] = nums[0]
        dp[1] = max(nums[0],nums[1])
        for i in range(2, len(nums)):
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
        return dp[len(nums) - 1]

dp数组表示偷到第i个房间最多偷了多少钱，

第i个房间最多偷了多少钱为偷与不偷当前房间的金额最大的那个

class Solution:
    def rob(self, nums: List[int]) -> int:
        #dp 偷到第i个房间，最多偷了多少钱
        #dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
        if len(nums) == 1:
            return nums[0]
        if len(nums) == 2:
            return max(nums[0], nums[1])
        dp = [0] * (len(nums))
        dp[0] = nums[0]
        dp[1] = max(nums[0],nums[1])
        # 走第一个房屋，不走最后一个
        for i in range(2, len(nums) - 1):
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
        candidate_1 = dp[len(nums) - 2]
        # 不走第一个，走最后一个
        dp = [0] * (len(nums))
        dp[1] = nums[1]
        dp[2] = max(nums[1], nums[2])
        for i in range(3, len(nums)):
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
        candidate_2 = dp[len(nums) - 1]
        return max(candidate_1, candidate_2)

不能同时偷首尾，那么就分两种情况考虑，偷第一家 不偷最后一家和不偷第一家，偷最后一家。

两个取最大值

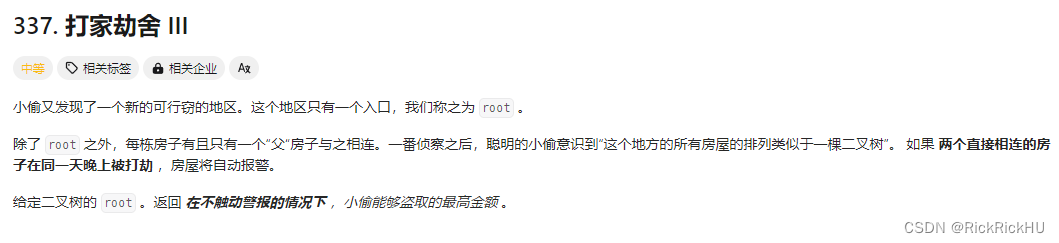
动态规划，房间连成树了，偷不偷呢？| LeetCode：337.打家劫舍3_哔哩哔哩gbilibilig

根本想不到

class Solution:
    # dp[0]表示不偷当前节点，能盗取的最大值, dp[1]表示偷当前节点， 能盗取的最大值
    def traversal(self, cur):
        if cur == None:
            return [0,0]
        left_dp = self.traversal(cur.left)
        right_dp = self.traversal(cur.right)
        # 当前节点偷的最大值 为当前节点的值加上左孩子不偷的最大值和右孩子不偷的最大值
        candidate_1 = cur.val + left_dp[0] + right_dp[0]
        # 当前节点不偷的最大值 为左孩子偷与不偷 能盗取的最大值和右孩子偷与不偷 能盗取的最大值
        candidate_2 = max(left_dp[0], left_dp[1]) + max(right_dp[0], right_dp[1])
        return (candidate_2, candidate_1)
    def rob(self, root: Optional[TreeNode]) -> int:
        u,v = self.traversal(root)
        return max(u,v)