🤵♂️ 个人主页: @AI_magician
📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。
👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!🐱🏍

摘要: 本系列旨在普及那些深度学习路上必经的核心概念,文章内容都是博主用心学习收集所写,欢迎大家三联支持!本系列会一直更新,核心概念系列会一直更新!欢迎大家订阅
该文章收录专栏
[✨— 《深入解析机器学习:从原理到应用的全面指南》 —✨]
问题归约法(Problem Reduction)
问题归约(problem reduction)是另一种基于状态空间的问题描述与求解方法。已知问题的描述,通过一系列变换把此问题最终变为一个本原问题集合;这些本原问题的解可以直接得到,从而解决了初始问题
问题归约表示的组成部分:
- 一个初始问题描述;
- 一套把问题变换为子问题的操作符;
- 一套本原问题描述。
问题归约的实质:
从目标(要解决的问题)出发逆向推理,建立子问题以及子问题的子问题,直至最后把初始问题归约为一个平凡的本原问题集合。
下面是问题归约法的一般步骤:
- 确定目标问题:明确要解决的原始问题是什么,以及需要得到的解决方案是什么。
- 识别子问题:分析原始问题,并确定可以将其分解为哪些较简单的子问题。子问题应该与原始问题相关,并且解决子问题可以为解决原始问题提供有用的信息。
- 定义转换规则:确定如何将原始问题转化为子问题。这包括定义问题之间的关系和转换过程,以确保转换后的子问题仍然保持原始问题的特性。
- 解决子问题:使用合适的方法或技术解决子问题。这可能涉及使用特定的算法、数学模型、启发式搜索等。
- 合并子问题的解:将子问题的解整合在一起,以得到原始问题的解。这可能需要将子问题的解进行组合、合并或进一步处理。
- 验证和优化解决方案:对得到的解决方案进行验证,确保它满足原始问题的要求。如果需要,可以对解决方案进行优化或调整。
我们以圆盘梵塔难题为例,
有3个柱子(1,2和3)和3个不同尺寸的圆盘(A,B和C)。在每个圆盘的中心有个孔,圆盘可以堆叠在柱子上。最初,全部3个圆盘都堆在柱子1上:最大的圆盘 C在底部,最小的圆盘A在顶部。要求把所有圆盘都移到柱子3上,每次只许移动一个,而且只能先搬动柱子顶部的圆盘,还不许把尺寸较大的圆盘堆放在尺寸较小的圆盘上。这个问题的初始配置和目标配置如图 2.3所示。
如果采用状态空间法来求解这个问题,其状态空间图含有 27个节点,每个节点代表柱子上圆盘的一种正当配置。

也可以用问题归约法来求解此问题。对图所示的原始问题从目标出发逆向推理,其过程如下;
(1)要把所有圆盘都移至柱子3,必须首先把圆盘C移至柱子3;而且在移动圆盘C至柱子3之前,要求柱子3必须是空的。
(2)只有在移开圆盘A和B之后,才能移动圆盘 C;而且圆盘A和B最好不要移至柱子3,否则就不能把圆盘 C移至柱子3。因此,首先应该把圆盘 A和B移到柱子2上。
(3)然后才能够进行关键的一步,把圆盘C从柱子1移至柱子3,并继续解决难题的其余部分。

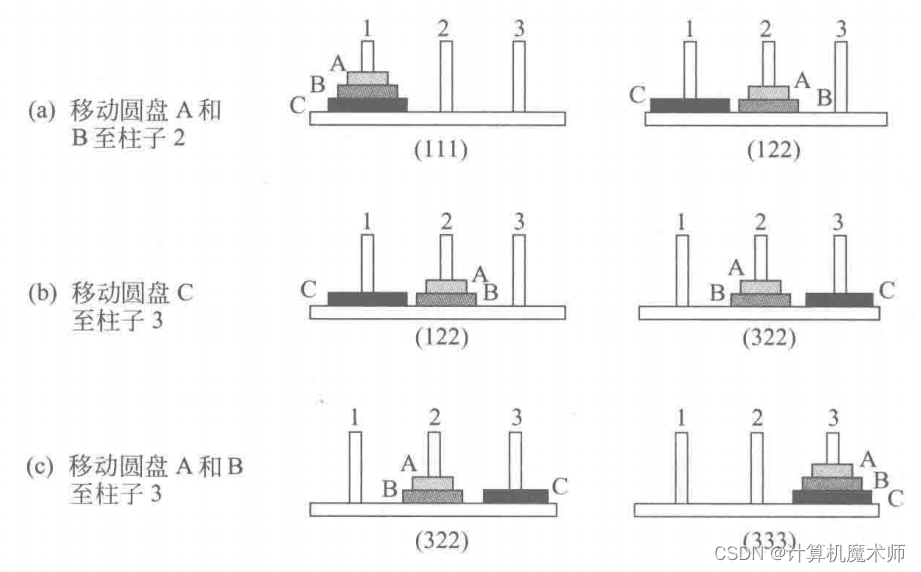
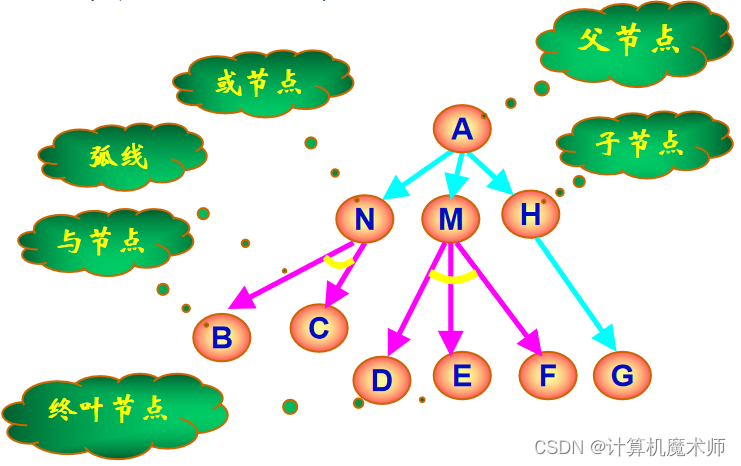
梵塔问题归约图(与或图)如下(用三元空间来描述问题)

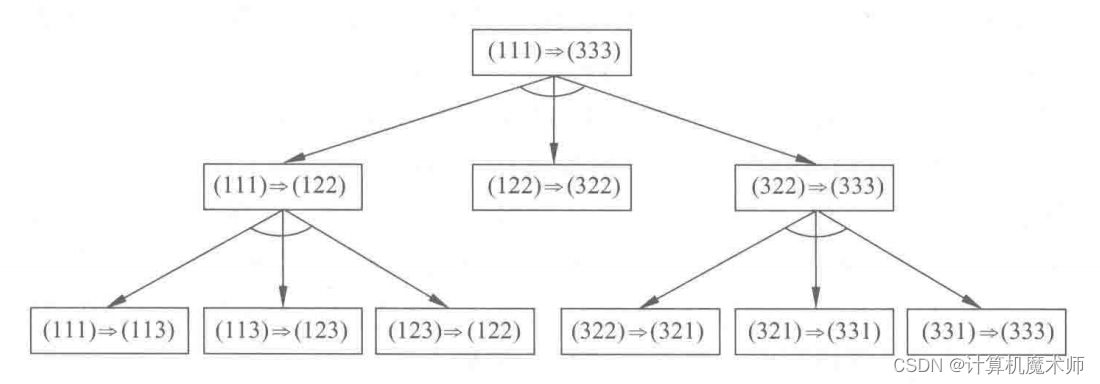
归约图(与或图)解释
一些关于与或图的术语
可解节点的一般定义
终叶节点是可解节点(因为它们与本原问题相关联),如果某个非终叶节点含有或后继节点,那么只要有一个后继节点是可解的时,此非终叶节点就是可解的。
如果某个非终叶节点含有与后继节点,那么只有其全部后继节点为可解时,此非终叶节点才是可解的。不可解节点的一般定义
没有后裔的非终叶节点为不可解节点如果某个非终叶节点含有或后继节点,那么只有当其全部后裔为不可解时,此非终叶节点才是不可解的。
如果某个非终叶节点含有与后继节点,那么只要好当其后裔有一个为不可解时,此非终叶节点就是不可解的。
谓词/符号逻辑(Symbolic Logic)
逻辑语句:一种形式语言,它能够把逻辑论证符号化,并用于证明定理,求解问题。
形式语言:严格地按照相关领域的特定规则,以数学符号(符号串)形式描述该领域有关客体的表达式。
语法和语义
基本符号:谓词符号、变量符号、函数符号、 常量符号、括号和逗号


在求解问题时,可把问题表示为一个有待证明的问题或定理,然后用消解原理和消解反演过程来证明。
在证明时,采用推理规则进行正向搜索, 使问题(定理)最终获得证明。另一种策略是采用反演证明来证明某个定理的否定是不成立的。首先假定该定理的否定是正确的,接着证明由公理和假定的定理之否定所组成的集合是不成立的,即导致矛盾的结论
通过逻辑推理和运用消解原理来求解证明。我们首先需要用谓词进行知识表示,以下是一个谓词的例子
设有如下语句,请用相应的谓词公式分别把他们表示出来 (要注意属性、行为、个体的区别)
1)有人每天下午都去打篮球。
2)有的人喜欢梅花,有的人喜欢菊花,有的人既喜欢梅花又喜欢菊花
1.) 有人每天下午都去打篮球。
解:定义谓词 P(x):
x是人 B(x):x打篮球 A(y):y是下午
将知识用谓词表示为:(A(y)→B(x)∧P(x))
2.) 老李每天下午都去打篮球。
解:定义谓词 d
P(x): x是人
L(x,y): x喜欢 y
其中,y 的个体域是(梅花,菊花)(注意个体域)
将知识用谓词表示为 :
$(Ex)(P(x)->L(x,梅花) ∨ L(x,菊花)∨ L(x,梅花)∧ L(x,菊花)) $
在更复杂的问题,我们需要掌握用消解/归结原理得到目标公式,消解是一种可用于一定的子句公式的重要推理规则,(对谓词演算公式进行分解和化简,消去一些符号,以求得导出子句,又称归结。)
以下是一些基本定义
子句:由文字的析取组成的合式公式。
文字:一个原子公式及其否定。
任一谓词演算公式可以化成一个子句集。变换过程如下:
- 消去蕴涵符号
只应用∨和∼,以∼ A ∨ B替换 A→B - 减少否定符号的辖域
每个否定符号最多只用到一个谓词符号上,并反复应用狄⋅ 摩根定律 - 对变量标准化
在任一量词辖域内,受该量词约束的变量称为一哑元(虚构变量),它可以在该辖域内处处统一的被另一个没有出现过的任意变量所代替,而不改变公的真值。
合式公式中变量的标准化意味着对哑元改名以保证每个量词都有其唯一的哑元 - 消去存在量词
从一个公式消去一个存在量词的一般规则是以一个Skolem函数1代替每个出现的存在量词的量化变量,而这个Skolem函数的变量就是由那些全称量词所约束的全称量词量化变量,这些全称量词的辖域包括要被消去的存在量词的辖域在内
如果要消去的存在量词不在任何一个全称量词的辖域内,那么就用不含变量的Skolem函数即常量
Skolem函数所使用的函数符号必须是新的 - 化为前束型
把所有全称量词移到公式的左边,并使每个量词的辖域包括这个量词后面公式的整个部分,所得公式称为前束型。前束型公式由前缀和母式组成,前缀由全称量词串组成,母式由没有量词的公式组成 - 把母式化为合取范式
任何母式都可写成由一些谓词公式和谓词公式的否定的析取的有限集组成的合取,这种母式叫做合取范式 - 消去全称量词
- 消去连词符号∧
用{ A , B } 代替( A , B ) (A,B)(A,B),以消去∧ - 更换变量名称
可以更换变量符号的名称,使一个变量符号不出现在一个以上的子句中
以下是基本定律(联接词的优先顺序:非~、合取∧、析取∨、蕴含)
(1) 否定之否定: ~(~P)等价于P
(2) P∨Q等价于~P=>Q
(3) 狄·摩根定律: ~(P∨Q)等价于~P∧~Q
~(P∧Q)等价于~P∨~Q
(4) 分配律: P∧(Q∨R)等价于(P∧Q)∨(P∧R)
P∨(Q∧R)等价于(P∨Q)∧(P∨R)
(5) 交换律: P∧Q等价于Q∧P
P∨Q等价于Q∨P
(6) 结合律: (P∧Q)∧R等价于P∧(Q∧R)
(P∨Q)∨R等价于P∨(Q∨R)
(7) 逆否律: P=>Q等价于~Q=>~P(8) ~(∃x)P(x) 等价于 (∀ x)[~P(x)]
~(∀ x)P(x) 等价于 (∃ x)[~P(x)](9) (∀ x)[P(x)∧Q(x)] 等价于 (∀ x)P(x)∧(∀ x)Q(x)
(∀ x)[P(x)∨Q(x)] 等价于 (∀ x)P(x)∨(∀ x)Q(x)(10) (∀ x)P(x) 等价于 (∀ y)P(y)
(∃ x)P(x) 等价于 (∃ y)P(y)
得到子句集后后续有三个重要的问题求解方法需要重点掌握
- 消解推理规则(根据已有的式子析取推理)
- 含有变量的消解式(根据基子句推理的推广、原理一样,需要额外使变量相等)
- 消解反演求解过程(将要证明的命题,将其否定添加到命题公式集,如产生矛盾为真、否则为假)
消解反演求解例子一(证明一个子句):
设事实的公式集合
{ P,(P∧Q)
→
\rightarrow
→ R,
(S∨T)
→
\rightarrow
→ Q,T },
证明:R
否定结论 ,将公式化为子句,得子句集:
{ P,~P∨~ Q∨R,
~S∨Q,~ T∨Q ,T ,
~R }
这里除了用列出结论之外还可以用消解反演树

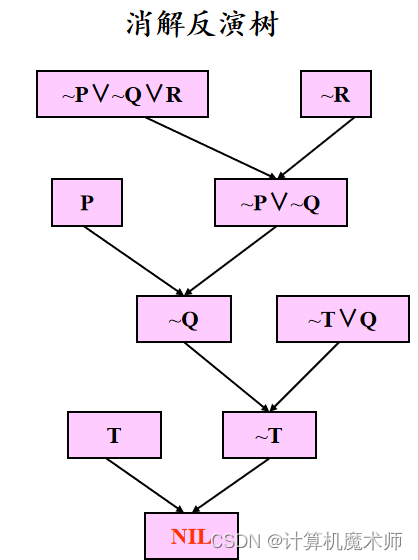
消解反演:
给出一个公式集合S 和目标公式L,通过反证或反演来求证目标公式 L ,其证明步骤如下:
否定L,得∼ L
把∼ L添加到S 中
把新产生的集合{ ∼ L , S } 化成子句集
应用消解原理,推导出一个表示矛盾的空子句反演求解过程:
用反演树求取对某个问题的答案
- 把由目标公式的否定产生的每个子句添加到目标公式否定之否定的子句中,形成重言式
- 按照反演树,执行和以前相同的消解,直至在根部得到某个子句为止
- 用根部的子句作为一个回答语句
答案求取涉及把一棵根部有NIL的反演树变换为在根部带有可用答案的某个语句的一棵证明树
再来一个例子(反演求解 证明一个公式),建议动手做做
已知
1)能够阅读的都是有文化的。
2)海豚是没有文化的。
3)某些海豚是有智能的。
用归结原理证明:某些有智能的并不能阅读。
解
证明:
已知谓词:R(x)表示x能阅读, L(x)表示有文化,D(x)表示x是海豚,I(x)表示智慧的。
则将条件与目标用谓词公式表示:
(1) ∀x(R(x)→L(x))
(2) ∀x(D(x)→¬L(x))
(3) ∃x(D(x)∧I(x))
把要求证的结论用谓词公式表示出来并否定,得:
(4) ∃x(I(x)∧¬R(x))
把上述公式化成子句集:
(1) ¬R(x)∨L(x)
(2) ¬D(y)∨¬L(y)
(3) D(a)
(4) I(a)
(5) ¬I(z)∨R(z)
应用归结原理进行归结:
(6) ¬L(a) (2),(3)归结
(7) ¬R(a) (1),(6)归结
(8) R(a) (4),(5)归结
(9) NIL (7),(8)归结

🤞到这里,如果还有什么疑问🤞
🎩欢迎私信博主问题哦,博主会尽自己能力为你解答疑惑的!🎩
🥳如果对你有帮助,你的赞是对博主最大的支持!!🥳