文章目录
- 1.双指针
- 2.位运算
- 3.离散化
- 4.区间合并
1.双指针
双指针的算法可以优化时间复杂度,双指针,指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个相同方向( 快慢指针 )或者相反方向( 对撞指针 )的指针进行扫描,从而达到相应的目的。将双层暴力循环O(n^2)优化到O(n),所以双指针算法最核心的用途就是优化时间复杂度。双指针是比较常见的把,直接看例子既可以。
给定一个长度为 n 的整数序列,请找出最长的不包含重复的数的连续区间,输出它的长度。
输入格式
第一行包含整数 n。
第二行包含 n 个整数(均在 0∼1050∼105 范围内),表示整数序列。
输出格式
共一行,包含一个整数,表示最长的不包含重复的数的连续区间的长度。
数据范围
1≤n≤1051≤n≤105
输入样例:
5 1 2 2 3 5输出样例:
3
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N],s[N];
int main()
{
cin>>n;
for(int i = 0;i<n;i++) cin>>a[i];
int res = 0;
for(int i = 0,j=0;i<n;i++)
{
s[a[i]]++;
while(s[a[i]]>1)
{
s[a[j]]--;
j++;
}
res = max(res,i-j+1);
}
cout<<res<<endl;
return 0;
}
2.位运算
位运算也是非常常见的,位运算就是直接对整数在内存中的二进制位进行 操作,这里简单过一下即可,同时对于这部分不太熟悉的,建议先熟悉一下位运算的相关操作,以及整数二进制存储的内容
常见的有:1.比如求一个数n以二进制方式表示,第k位数字是几:把第k位移到最后一位既n>>k,然后看此时的个位是几,&1即可
2.lowbit(x):返回x的最后一位1。lowbit()的实现就是在x&-x. 怎么理解-x:对于一个整数的负数是原数的补码,相当于 -x=~x+1
也就是说x&-x相当于x&(~x+1)

可以统计1的个数
题目练习:
给定一个长度为 nn 的数列,请你求出数列中每个数的二进制表示中 11 的个数。
输入格式
第一行包含整数 nn。
第二行包含 nn 个整数,表示整个数列。
输出格式
共一行,包含 nn 个整数,其中的第 ii 个数表示数列中的第 ii 个数的二进制表示中 11 的个数。
数据范围
1≤n≤1000001≤n≤100000,
0≤数列中元素的值≤1090≤数列中元素的值≤109输入样例:
5 1 2 3 4 5输出样例:
1 1 2 1 2
#include <iostream>
using namespace std;
int lowbit(int x)
{
return x&-x;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int x;
cin>>x;
int res = 0;
while(x)
{
x-=lowbit(x);
res++;
}
cout<<res<<' ';
}
return 0;
}
3.离散化
这里的离散化指的是特指整数有序的离散化,保序的离散化:值域比较大,但是个数却很少,类似哈希,以里面的值为下标来做即可,不需要开很大的数组,只需要进行映射即可。一个问题是去重,另一个问题是如何具体算出a[i]离散化的值是多少,a是有序的自然可以通过二分进行查找,而去重可以利用unique函数
假定有一个无限长的数轴,数轴上每个坐标上的数都是 0。
现在,我们首先进行 n 次操作,每次操作将某一位置 x 上的数加 c。
接下来,进行 m 次询问,每个询问包含两个整数 l 和 r,你需要求出在区间 [l,r][l,r] 之间的所有数的和。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含两个整数 x 和 c。
再接下来 m 行,每行包含两个整数 l 和 r。
输出格式
共 m行,每行输出一个询问中所求的区间内数字和。
数据范围
−109≤x≤109−109≤x≤109,
1≤n,m≤1051≤n,m≤105,
−109≤l≤r≤109−109≤l≤r≤109,
−10000≤c≤10000输入样例:
3 3 1 2 3 6 7 5 1 3 4 6 7 8输出样例:
8 0 5
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 300010;
int n, m;
int a[N];
int s[N];
vector<int> alls;
vector<pair<int, int>> add, query;
int find(int x) 、
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
{
int x, c;
scanf("%d%d", &x, &c);
add.push_back({x, c});
alls.push_back(x);
}
for (int i = 1; i <= m; i++)
{
int l , r;
scanf("%d%d", &l, &r);
query.push_back({l, r});
alls.push_back(l);
alls.push_back(r);
}
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
for (auto item : add)
{
int x = find(item.first);
a[x] += item.second;
}
for (int i = 1; i <= alls.size(); i++) s[i] = s[i-1] + a[i];
for (auto item : query)
{
int l = find(item.first);
int r = find(item.second);
printf("%d\n", s[r] - s[l-1]);
}
return 0;
}
4.区间合并
简单理解为2个有交集的区间合并成一个更大的区间即可,区间合并就是快速让我们把有交集的区间进行合并。
区间的合并先按左端点进行排序,然后去进行维护: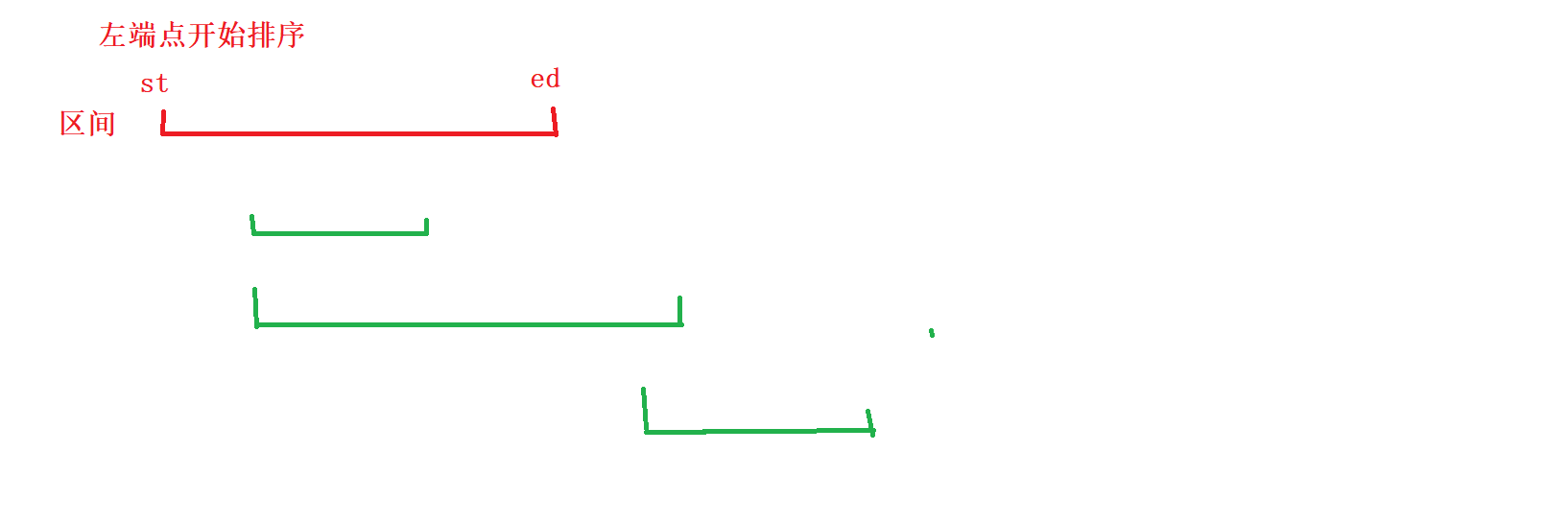
给定 n 个区间 [li,ri][li,ri],要求合并所有有交集的区间。
注意如果在端点处相交,也算有交集。
输出合并完成后的区间个数。
例如:[1,3][1,3] 和 [2,6][2,6] 可以合并为一个区间 [1,6][1,6]。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含两个整数 l和 r。
输出格式
共一行,包含一个整数,表示合并区间完成后的区间个数。
数据范围
1≤n≤1000001≤n≤100000,
−109≤li≤ri≤109−109≤li≤ri≤109输入样例:
5 1 2 2 4 5 6 7 8 7 9输出样例:
3
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n;
typedef pair<int,int> PII;
vector<PII> segs;
void merge(vector<PII>& segs)
{
vector<PII> res;
sort(segs.begin(),segs.end());
int st = -2e9,ed = -2e9;
for(auto seg:segs)
{
if(ed<seg.first)
{
if(st!=-2e9) res.push_back({st,ed});
st = seg.first,ed = seg.second;
}
else ed = max(ed,seg.second);
}
if(st!=-2e9) res.push_back({st,ed});
segs = res;
}
int main()
{
cin>>n;
for(int i = 0;i<n;i++)
{
int l,r;
cin>>l>>r;
segs.push_back({l,r});
}
merge(segs);
cout<<segs.size()<<endl;
return 0;
}
合并区间比较常见把:比如leetcode的56合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> result;
sort(intervals.begin(),intervals.end());
int begin = intervals[0][0],end = intervals[0][1];
for(size_t i = 0;i<intervals.size();i++)
{
if(intervals[i][0]>end)
{
result.push_back({begin,end});
begin = intervals[i][0];
end = intervals[i][1];
}
else
{
end = max(end,intervals[i][1]);
}
}
result.push_back({begin,end});
return result;
}
};