目录
- 前言
- NeRF
- 神经辐射场
- 体渲染
- 连续体渲染
- 体渲染离散化
- 方法
- 位置编码
- 分层采样
- 体渲染推导公式(1)到公式(2)
- 部分代码解读
- 相机变换(重要!)
- Mip-Nerf
- To do
- Instant-NGP
- To do
前言
NeRF是NeRF系列的开山之作,将三维场景隐式的表达为神经网络的权重用于新视角合成。
MipNeRF和Instant NGP分别代表了NeRF的两个研究方向,前者是抗锯齿,代表着渲染质量提升方向;后者是采用多分辨率哈希表用于加速NeRF的训练与推理速度。
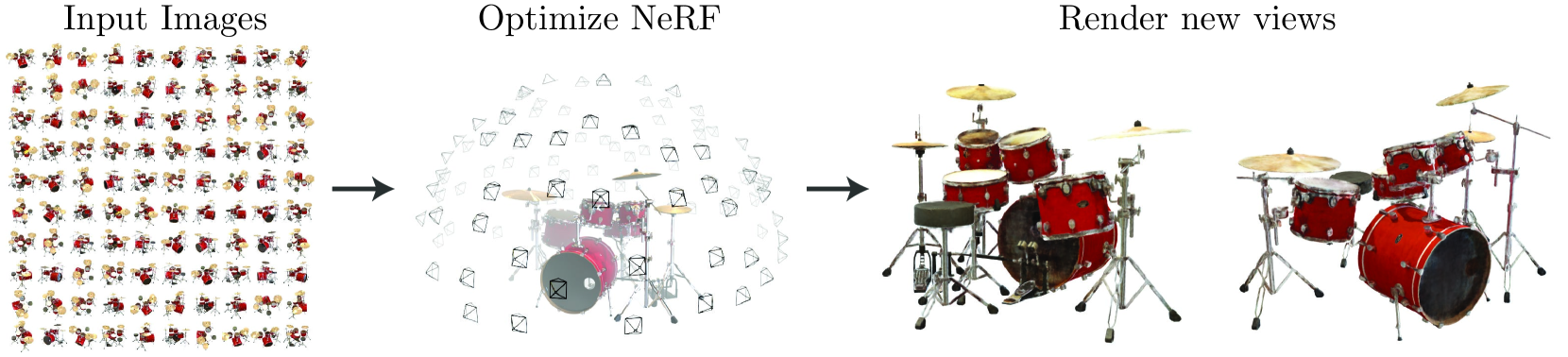
NeRF
Title:NeRF: Representing Scenes asNeural Radiance Fields for View Synthesis
Code:nerf-pytorch
From:ECCV 2020 Oral - Best Paper Honorable Mention
神经辐射场
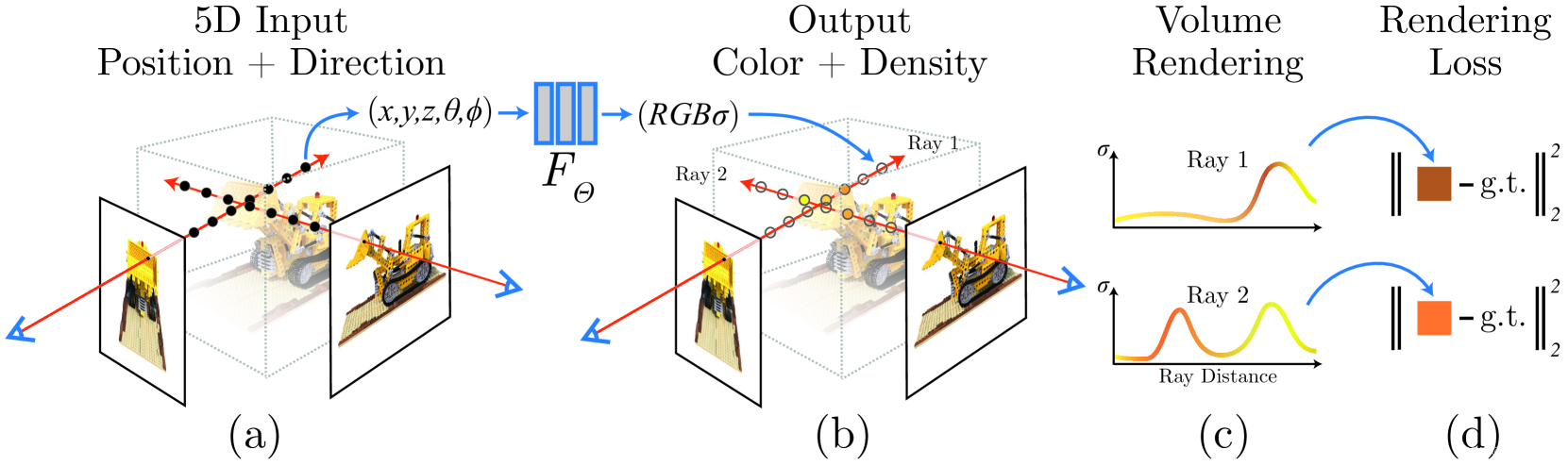
辐射场可以理解光线场,给定多张带有相机内外参的二维图片,从摄像机出发,引出到每一个像素的光线,通过对这条光线经历过的空间点的颜色
c
c
c和体密度体密度
σ
\sigma
σ进行累积,以得到二维图片上像素点的颜色,从而实现端到端训练。在这个过程中,没有显式的三维结构,如点云、体素或者Mesh,而是通过神经网络的权重
F
θ
F_{\theta}
Fθ将三维场景连续的存储起来,通过空间位置(三维点
[
x
,
y
,
z
]
[x,y,z]
[x,y,z])和视角方向(球坐标系下的极角和方位角
[
θ
,
ϕ
]
[\theta,\phi]
[θ,ϕ])作为查询条件,查询出给定摄像机下的光线所经过的空间点颜色
c
c
c和体密度
σ
\sigma
σ,通过**体渲染(Volume Rendering)**得到该条光线对应像素点的颜色。
体渲染

沿着视角方向的光线上的点P可以用上图来表示,尽管论文中提到视角方向是使用 θ , ϕ \theta,\phi θ,ϕ来表示的,但代码中还是使用单位向量 d d d来表示的。
连续体渲染
体渲染实际上就是将视线r上所有的点通过某种方式累计投射到图像上形成像素颜色
C
(
r
)
C(r)
C(r)的过程:
C
(
r
)
=
∫
t
n
t
f
T
(
t
)
σ
(
r
(
t
)
)
c
(
r
(
t
)
,
d
)
d
t
where
T
(
t
)
=
exp
(
−
∫
t
n
t
σ
(
r
(
s
)
)
d
s
)
(1)
{C}(\boldsymbol{r})=\int_{t_n}^{t_f} T(t) \sigma(\boldsymbol{r}(t)) \boldsymbol{c}(\boldsymbol{r}(t), \boldsymbol{d}) dt \\ \text{where } T(t)=\exp \left(-\int_{t_n}^t \sigma(\boldsymbol{r}(s)) d s\right)\tag{1}
C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dtwhere T(t)=exp(−∫tntσ(r(s))ds)(1)
其中,
c
(
r
(
t
)
,
d
)
\boldsymbol{c}(\boldsymbol{r}(t), \boldsymbol{d})
c(r(t),d)为三维点
r
(
t
)
r(t)
r(t)从
d
d
d这个方向看到的颜色值;
σ
(
r
(
t
)
)
\sigma(\boldsymbol{r}(t))
σ(r(t))为体密度函数,反映的是该三维点的物理材质吸收光线的能力;
T
(
t
)
T(t)
T(t)反映的是射线上从
t
n
t_n
tn到
t
t
t的累积透射率。tn和tf首先确定了nerf的边界,而不至于学习到无穷远;其次避免了光心到近景范围内无效采样。
直观上理解σ,可以解释为每个三维点吸收光线的能力,光经过该点,一部分被吸收,一部分透射,光的强度(可以理解为
T
(
t
)
T(t)
T(t)) 在逐渐减小,当光强为0时,后面的三维点即便可以吸收颜色,也不会对像素颜色有贡献。指数函数保证了随着σ的累积,光的强度从1逐渐减为0。
体渲染离散化
其实就是函数离散化的形式,将tn到tf拆分成N个均匀的分布空间,从每个区间中随机选取一个样本ti:
t i ∼ U [ t n + i − 1 N ( t f − t n ) , t n + i N ( t f − t n ) ] i 从1到N t_i \sim \mathcal{U}\left[t_n+\frac{i-1}{N}\left(t_f-t_n\right), t_n+\frac{i}{N}\left(t_f-t_n\right)\right] \quad i \text{ 从1到N} ti∼U[tn+Ni−1(tf−tn),tn+Ni(tf−tn)]i 从1到N
然后将连续体渲染公式离散化:
C
^
(
r
)
=
∑
i
=
1
N
T
i
(
1
−
exp
(
−
σ
i
δ
i
)
)
c
i
where
T
i
=
exp
(
−
∑
j
=
1
i
−
1
σ
j
δ
j
)
(2)
\hat{C}(\mathbf{r})=\sum_{i=1}^N T_i\left(1-\exp \left(-\sigma_i \delta_i\right)\right) \mathbf{c}_i \quad \tag 2 \\ \text{where } T_i=\exp \left(-\sum_{j=1}^{i-1} \sigma_j \delta_j\right)
C^(r)=i=1∑NTi(1−exp(−σiδi))ciwhere Ti=exp(−j=1∑i−1σjδj)(2)
where
T
i
=
exp
(
−
∑
j
=
1
i
−
1
σ
j
δ
j
)
T_i=\exp \left(-\sum_{j=1}^{i-1} \sigma_j \delta_j\right)
Ti=exp(−∑j=1i−1σjδj)
其中,
δ
i
=
t
i
+
1
−
t
i
\delta_i=t_{i+1}-t_i
δi=ti+1−ti 表示相邻采样点之间的距离
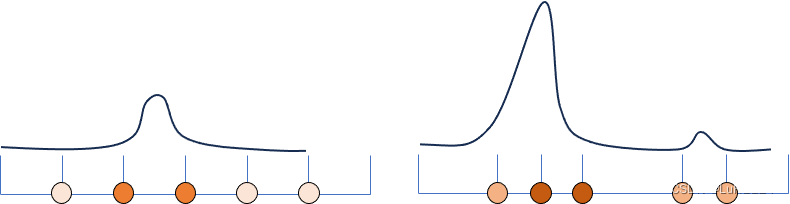
但均匀采样有明显的问题, 比如体密度较大的点如果在两个采样点之间,那么永远不可能采样到。从上图中可看出,左半张代表均匀采样,右半张代表真实分布,左边由于表面两侧被采样到,只能反应这个区间内可能存在表面,但估计的σ不一定准确。
作者提出了分层采样来试图解决这个问题。
方法
位置编码
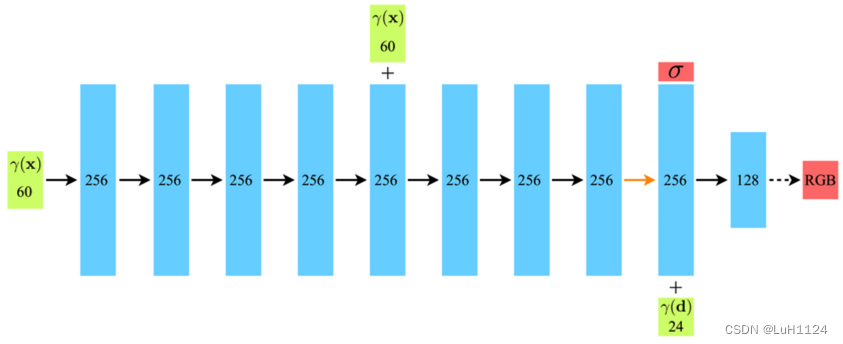
网络结构由如上图所示全连接网络组成,输入x,d分别分三维点的空间位置和视线方向。该三维点的体密度只与空间位置相关,颜色还和视角相关。
γ ( p ) = ( sin ( 2 0 π p ) , cos ( 2 0 π p ) , ⋯ , sin ( 2 L − 1 π p ) , cos ( 2 L − 1 π p ) ) \gamma(p)=\left(\sin \left(2^0 \pi p\right), \cos \left(2^0 \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right) γ(p)=(sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp))
还可以注意到γ(x)和γ(d)分别是对位置坐标和方向坐标的位置编码(标准正余弦位置编码),这是由于单纯坐标只能体现低频信息,位置编码可以有效的区分开两个距离很近的坐标(即低频接近但高频编码分开【但或许也有问题,离得特别近的两个点或许低频信息也不相似,私以为mipnerf考虑三维点邻域的区间,在一定程度上可以缓解】),从而帮助网络学习到高频几何和纹理细节。如下图所示,视角信息有效反应高光信息,位置编码有助于恢复高频细节。

分层采样
除了上述提到的均匀采样可能导致i真实表面难以正好采样到,还有均匀采样带来了很多无意义空间的无效采样,简单来说,只有空气的地方没必要进行采样,或者被遮挡区域(可见性问题,不可见区域也没必要采样,需要提前判断累积透射率是否为降为0)。
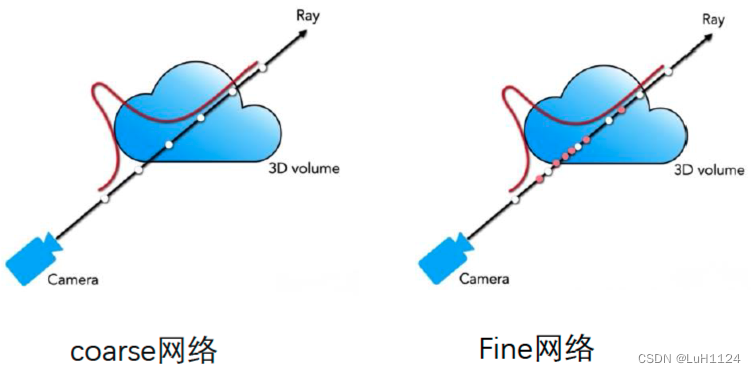
首先均匀采样可以得到crose color,wi可以理解为同条射线被采样的
N
c
N_c
Nc个三维点颜色的权重:
C
^
c
(
r
)
=
∑
i
=
1
N
c
w
i
c
i
,
w
i
=
T
i
(
1
−
exp
(
−
σ
i
δ
i
)
)
\widehat{C}_c(\mathbf{r})=\sum_{i=1}^{N_c} w_i c_i, \quad w_i=T_i\left(1-\exp \left(-\sigma_i \delta_i\right)\right)
C
c(r)=i=1∑Ncwici,wi=Ti(1−exp(−σiδi))
根据均匀采样点的权重值归一化后按重要性重新采样得到新的 n f n_f nf个位置
w ^ i = w i / ∑ j = 1 N c w j \widehat{w}_i=w_i / \sum_{j=1}^{N_c} w_j w i=wi/j=1∑Ncwj
最后损失函数可以表示为:
L = ∑ r ∈ R [ ∥ C ^ c ( r ) − C ( r ) ∥ 2 2 + ∥ C ^ f ( r ) − C ( r ) ∥ 2 2 ] \mathcal{L}=\sum_{\mathbf{r} \in \mathcal{R}}\left[\left\|\widehat{C}_c(\mathbf{r})-C(\mathbf{r})\right\|_2^2+\left\|\widehat{C}_f(\mathbf{r})-C(\mathbf{r})\right\|_2^2\right] L=r∈R∑[ C c(r)−C(r) 22+ C f(r)−C(r) 22]
这里为什么选用两个网络来分别做粗糙采样和精细采样,参考大佬【
】。crose网络是用于均匀采样的,包含更多的是低频信息的查询,而fine网络用于重要性采样,适用于三维点高频细节的查询,两个网络起到了类似滤波器的作用。
「待做实验验证!!!Todo」
体渲染推导公式(1)到公式(2)
首先,光线通过区间
[
0
,
t
+
d
t
)
[0, t+d t)
[0,t+dt) 的概率:
光线通过区间
[
0
,
t
+
d
t
)
[0, t+d t)
[0,t+dt) 的概率:
T
(
t
+
d
t
)
=
T
(
t
)
⋅
(
1
−
d
t
⋅
σ
(
t
)
)
\begin{aligned} \mathcal{T}(t+d t) & =\mathcal{T}(t) \cdot(1-d t \cdot \sigma(t)) \end{aligned}
T(t+dt)=T(t)⋅(1−dt⋅σ(t))
可以得到
T
(
t
+
d
t
)
−
T
(
t
)
d
t
≡
T
′
(
t
)
=
−
T
(
t
)
⋅
σ
(
t
)
\begin{aligned} \frac{\mathcal{T}(t+d t)-\mathcal{T}(t)}{d t} & \equiv \mathcal{T}^{\prime}(t)=-\mathcal{T}(t) \cdot \sigma(t) \end{aligned}
dtT(t+dt)−T(t)≡T′(t)=−T(t)⋅σ(t)
1
−
T
(
t
)
1-\mathcal{T}(t)
1−T(t) 为光线在区间
[
0
,
t
)
[0, t)
[0,t) 被终止的累积分布函数(CDF);
T
(
t
)
σ
(
t
)
\mathcal{T}(t) \sigma(t)
T(t)σ(t) 为其对应的概率密度函数 (PDF)
其中,
T
(
t
)
\mathcal{T}(t)
T(t) 为光线通过区间
[
0
,
t
)
[0, t)
[0,t) 透射率,也就是没被终止的概率,从1->0;
σ
(
t
)
\sigma(t)
σ(t) 为体密度函数;
d
t
⋅
σ
(
t
)
d t \cdot \sigma(t)
dt⋅σ(t) 为光线在
[
t
,
t
+
d
t
)
[t, t+d t)
[t,t+dt) 区间被吸收的概率,也就是被终止概率。
T
′
(
t
)
=
−
T
(
t
)
⋅
σ
(
t
)
T
′
(
t
)
T
(
t
)
=
−
σ
(
t
)
∫
a
b
T
′
(
t
)
T
(
t
)
d
t
=
−
∫
a
b
σ
(
t
)
d
t
log
T
(
t
)
∣
a
b
=
−
∫
a
b
σ
(
t
)
d
t
T
(
a
→
b
)
≡
T
(
b
)
T
(
a
)
=
exp
(
−
∫
a
b
σ
(
t
)
d
t
)
\begin{aligned} \mathcal{T}^{\prime}(t) & =-\mathcal{T}(t) \cdot \sigma(t) \\ \frac{\mathcal{T}^{\prime}(t)}{\mathcal{T}(t)} & =-\sigma(t) \\ \int_a^b \frac{\mathcal{T}^{\prime}(t)}{\mathcal{T}(t)} d t & =-\int_a^b \sigma(t) d t \\ \left.\log \mathcal{T}(t)\right|_a ^b & =-\int_a^b \sigma(t) d t \\ \mathcal{T}(a \rightarrow b) \equiv \frac{\mathcal{T}(b)}{\mathcal{T}(a)} & =\exp \left(-\int_a^b \sigma(t) d t\right) \end{aligned}
T′(t)T(t)T′(t)∫abT(t)T′(t)dtlogT(t)∣abT(a→b)≡T(a)T(b)=−T(t)⋅σ(t)=−σ(t)=−∫abσ(t)dt=−∫abσ(t)dt=exp(−∫abσ(t)dt)
T
(
a
→
b
)
\mathcal{T}(a \rightarrow b)
T(a→b) 表示光线通过
a
a
a 到
b
b
b 区间没被终止的概率,假设
[
a
,
b
)
[a,b)
[a,b) 共享
a
a
a点体密度和颜色
C
=
∫
0
D
T
(
t
)
⋅
σ
(
t
)
⋅
c
(
t
)
d
t
+
T
(
D
)
⋅
c
b
g
C=\int_0^D \mathcal{T}(t) \cdot \sigma(t) \cdot \mathbf{c}(t) d t+\mathcal{T}(D) \cdot \mathbf{c}_{\mathrm{bg}}
C=∫0DT(t)⋅σ(t)⋅c(t)dt+T(D)⋅cbg
c
b
g
c_{b g}
cbg 表示背景色彩
C ( a → b ) = ∫ a b T ( a → t ) ⋅ σ ( t ) ⋅ c ( t ) d t = σ a ⋅ c a ∫ a b T ( a → t ) d t = σ a ⋅ c a ∫ a b exp ( − ∫ a t σ ( u ) d u ) d t = σ a ⋅ c a ∫ a b exp ( − σ a u ∣ a t ) d t = σ a ⋅ c a ∫ a b exp ( − σ a ( t − a ) ) d t = σ a ⋅ c a ⋅ exp ( − σ a ( t − a ) ) − σ a ∣ a b = c a ⋅ ( 1 − exp ( − σ a ( b − a ) ) ) \begin{aligned} \boldsymbol{C}(a \rightarrow b) & =\int_a^b \mathcal{T}(a \rightarrow t) \cdot \sigma(t) \cdot \mathbf{c}(t) d t \\ & =\sigma_a \cdot \mathbf{c}_a \int_a^b \mathcal{T}(a \rightarrow t) d t \\ & =\sigma_a \cdot \mathbf{c}_a \int_a^b \exp \left(-\int_a^t \sigma(u) d u\right) d t \\ & =\sigma_a \cdot \mathbf{c}_a \int_a^b \exp \left(-\left.\sigma_a u\right|_a ^t\right) d t \\ & =\sigma_a \cdot \mathbf{c}_a \int_a^b \exp \left(-\sigma_a(t-a)\right) d t \\ & =\left.\sigma_a \cdot \mathbf{c}_a \cdot \frac{\exp \left(-\sigma_a(t-a)\right)}{-\sigma_a}\right|_a ^b \\ & =\mathbf{c}_a \cdot\left(1-\exp \left(-\sigma_a(b-a)\right)\right)\end{aligned} C(a→b)=∫abT(a→t)⋅σ(t)⋅c(t)dt=σa⋅ca∫abT(a→t)dt=σa⋅ca∫abexp(−∫atσ(u)du)dt=σa⋅ca∫abexp(−σau∣at)dt=σa⋅ca∫abexp(−σa(t−a))dt=σa⋅ca⋅−σaexp(−σa(t−a)) ab=ca⋅(1−exp(−σa(b−a)))
T ( a → c ) = = exp ( − [ ∫ a b σ ( t ) d t + ∫ b c σ ( t ) d t ] ) = exp ( − ∫ a b σ ( t ) d t ) exp ( − ∫ b c σ ( t ) d t ) = T ( a → b ) ⋅ T ( b → c ) \begin{aligned} \mathcal{T}(a \rightarrow c)= & =\exp \left(-\left[\int_a^b \sigma(t) d t+\int_b^c \sigma(t) d t\right]\right) \\ & =\exp \left(-\int_a^b \sigma(t) d t\right) \exp \left(-\int_b^c \sigma(t) d t\right) \\ & =\mathcal{T}(a \rightarrow b) \cdot \mathcal{T}(b \rightarrow c)\end{aligned} T(a→c)==exp(−[∫abσ(t)dt+∫bcσ(t)dt])=exp(−∫abσ(t)dt)exp(−∫bcσ(t)dt)=T(a→b)⋅T(b→c)
T n = T ( t n ) = T ( 0 → t n ) = exp ( − ∫ 0 t n σ ( t ) d t ) = exp ( ∑ k = 1 n − 1 − σ k δ k ) \mathcal{T}_n=\mathcal{T}\left(t_n\right)=\mathcal{T}\left(0 \rightarrow t_n\right)=\exp \left(-\int_0^{t_n} \sigma(t) d t\right)=\exp \left(\sum_{k=1}^{n-1}-\sigma_k \delta_k\right) Tn=T(tn)=T(0→tn)=exp(−∫0tnσ(t)dt)=exp(k=1∑n−1−σkδk)
C ( t N + 1 ) = ∑ n = 1 N ∫ t n t n + 1 T ( t ) ⋅ σ n ⋅ c n d t = ∑ n = 1 N ∫ t n t n + 1 T ( 0 → t n ) ⋅ T ( t n → t ) ⋅ σ n ⋅ c n d t = ∑ n = 1 N T ( 0 → t n ) ∫ t n t n + 1 T ( t n → t ) ⋅ σ n ⋅ c n d t = ∑ n = 1 N T ( 0 → t n ) ⋅ ( 1 − exp ( − σ n ( t n + 1 − t n ) ) ) ⋅ c n \begin{aligned} \boldsymbol{C}\left(t_{N+1}\right) & =\sum_{n=1}^N \int_{t_n}^{t_{n+1}} \mathcal{T}(t) \cdot \sigma_n \cdot \mathbf{c}_n d t \\ & =\sum_{n=1}^N \int_{t_n}^{t_{n+1}} \mathcal{T}\left(0 \rightarrow t_n\right) \cdot \mathcal{T}\left(t_n \rightarrow t\right) \cdot \sigma_n \cdot \mathbf{c}_n d t \\ & =\sum_{n=1}^N \mathcal{T}\left(0 \rightarrow t_n\right) \int_{t_n}^{t_{n+1}} \mathcal{T}\left(t_n \rightarrow t\right) \cdot \sigma_n \cdot \mathbf{c}_n d t \\ & =\sum_{n=1}^N \mathcal{T}\left(0 \rightarrow t_n\right) \cdot\left(1-\exp \left(-\sigma_n\left(t_{n+1}-t_n\right)\right)\right) \cdot \mathbf{c}_n\end{aligned} C(tN+1)=n=1∑N∫tntn+1T(t)⋅σn⋅cndt=n=1∑N∫tntn+1T(0→tn)⋅T(tn→t)⋅σn⋅cndt=n=1∑NT(0→tn)∫tntn+1T(tn→t)⋅σn⋅cndt=n=1∑NT(0→tn)⋅(1−exp(−σn(tn+1−tn)))⋅cn
T ( 0 → t n ) ⋅ ( 1 − exp ( − σ n ( t n + 1 − t n ) ) ) \mathcal{T}\left(0 \rightarrow t_n\right) \cdot\left(1-\exp \left(-\sigma_n\left(t_{n+1}-t_n\right)\right)\right) T(0→tn)⋅(1−exp(−σn(tn+1−tn)))表示光线正好在 t N + 1 t_{N+1} tN+1位置的颜色的权重(**透射率*该点的颜色吸收率=该点颜色的贡献率,对应代码中的weights,代码中的 α \alpha α指代 1 − e x p ( − σ ∗ δ ) ∗ ∗ 1-exp(-\sigma*\delta)** 1−exp(−σ∗δ)∗∗)
C ( t N + 1 ) = ∑ n = 1 N T n ⋅ ( 1 − exp ( − σ n δ n ) ) ⋅ c n , where T n = exp ( ∑ k = 1 n − 1 − σ k δ k ) \boldsymbol{C}\left(t_{N+1}\right)=\sum_{n=1}^N \mathcal{T}_n \cdot\left(1-\exp \left(-\sigma_n \delta_n\right)\right) \cdot \mathbf{c}_n, \quad \\ \text{where} \quad \mathcal{T}_n=\exp \left(\sum_{k=1}^{n-1}-\sigma_k \delta_k\right) C(tN+1)=n=1∑NTn⋅(1−exp(−σnδn))⋅cn,whereTn=exp(k=1∑n−1−σkδk)
部分代码解读
相机变换(重要!)
-
关于nerf相机方向的解读
-
关于llff格式数据使用的NDC空间解读
简单来说就是针对不同种类的数据在不同的空间进行计算,如360度合成数据lego(直接从相机坐标系变换到世界坐标系下)或者无界数据llff(NDC空间能将近远景范围限制在0-1之间)