122.买卖股票的最佳时机 II
初始思路:
这道题解题的时候比较像在找规律,发现只要计算这个过程中的两数之差然后相加即可。
题解复盘:
可以更加清晰的发现如何从题意中获得贪心的思路。
如何贪心:局部最优:收集每天的正利润,全局最优:求得最大利润。

// 贪心思路
class Solution {
public int maxProfit(int[] prices) {
int result = 0;
for (int i = 1; i < prices.length; i++) {
result += Math.max(prices[i] - prices[i - 1], 0);
}
return result;
}
}55.跳跃游戏
初始思路:
感觉在这个过程中只要每一个数都大于等于1的话是一定可以到达最后一个格子的,关键在于对出现0格子的处理,难以处理。
题解复盘:
怎么跳跃不重要,关键在于覆盖范围。
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
覆盖范围 = i+nums[i].
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
class Solution {
public boolean canJump(int[] nums) {
int cover = 0;
if(nums.length==1){return true;}
for(int i = 0;i<=cover;i++){
cover = Math.max(cover,i+nums[i]);
if(cover >= nums.length-1){return true;}
}
return false;
}
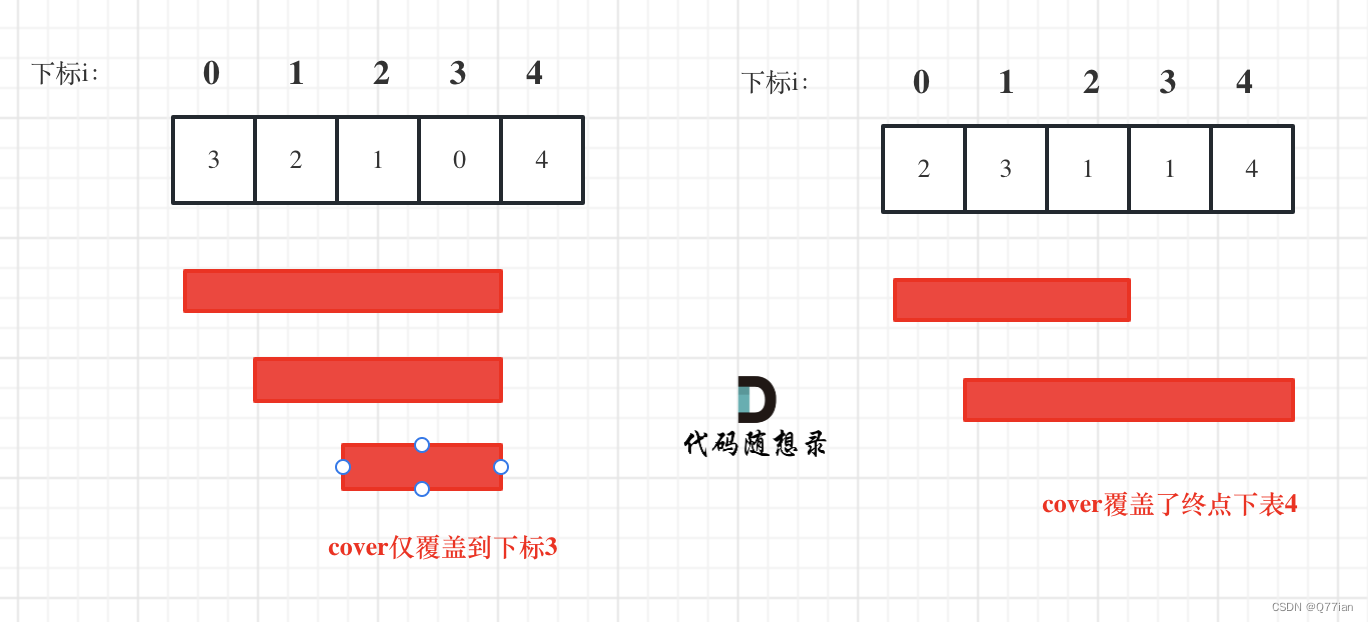
}注意for循环中一定是cover而不是nums.length!

不然对于这种情况,i就会遍历到数组的最后一个元素4,此时i+nums[i] = 8也大于等于nums.length-1,之前对于结果的输出限制就不起作用了。
45.跳跃游戏||
初始思路&&题解复盘:
不得不说这个思路是真的挺难想的;
贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最少步数。
要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最少步数!
具体实现就是在当前覆盖范围走到尽头时,如果还没有走到终点,就更新下一个覆盖范围,并且更新result,如果走到终点就进行一个break。
class Solution {
public int jump(int[] nums) {
if(nums.length==1){return 0;}
int cover = 0;
int next = 0;
int count = 0;
for(int i = 0;i<nums.length;i++){
next= Math.max(next,i+nums[i]);
if(cover>=nums.length-1){break;}
if(i==cover){
if(cover<nums.length-1){
count++;
cover = next;
}
}
}
return count;
}
}