多维函数求解的基本概念
- 多维函数
- 最优化问题
- 最优化算法
- 最优化问题的类型
- 最优化算法的分类
- 常用的多维函数求解方法
- 结语
多维函数
多维函数是指定义在 R n \mathbb{R}^n Rn 上的函数,其中 n n n 是函数的维数。例如, f ( x , y ) = x 2 + y 2 f(x, y) = x^2 + y^2 f(x,y)=x2+y2 是一个二维函数, f ( x , y , z ) = x 2 + y 2 + z 2 f(x, y, z) = x^2 + y^2 + z^2 f(x,y,z)=x2+y2+z2 是一个三维函数。
最优化问题
最优化问题是指在给定的约束条件下,找到函数 f ( x ) f(x) f(x) 的最大值或最小值。
最优化算法
最优化算法是指用于求解最优化问题的算法。
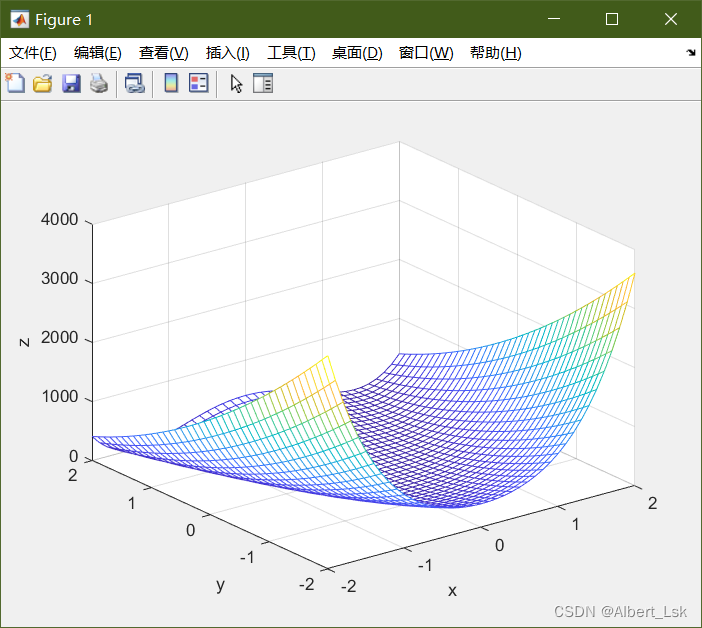
最优化问题的类型
根据函数 f ( x ) f(x) f(x) 的性质,最优化问题可以分为以下几种类型:
- 无约束最优化问题
无约束最优化问题是指没有任何约束条件的最优化问题。例如,求函数 f ( x ) = x 2 f(x) = x^2 f(x)=x2 的最小值。
- 有约束最优化问题
有约束最优化问题是指存在约束条件的最优化问题。例如,求函数 f ( x ) = x 2 f(x) = x^2 f(x)=x2 的最小值,其中 x ≥ 0 x \ge 0 x≥0。
最优化算法的分类
根据求解最优化问题的策略,最优化算法可以分为以下几种类型:
- 直接法
直接法是指直接求解最优化问题的最优解。例如,牛顿法就是一种直接法。
- 迭代法
迭代法是指通过迭代的方式逐步逼近最优解。例如,梯度下降法就是一种迭代法。
根据函数 f(x) 的性质,最优化算法可以分为以下几种类型:
- 凸优化问题
凸优化问题是指函数 f(x) 是凸函数,且约束条件是凸集。对于凸优化问题,存在唯一的全局最优解。
- 非凸优化问题
非凸优化问题是指函数 f(x) 是非凸函数,或约束条件是非凸集。对于非凸优化问题,可能存在多个局部最优解,甚至没有全局最优解。
常用的多维函数求解方法
常用的最优化算法包括以下几种:
- 梯度下降法
梯度下降法是一种简单易用的迭代方法。该方法的基本思想是,在当前点 ( x k , y k ) (x_k, y_k) (xk,yk) 处,沿着函数 f ( x ) f(x) f(x) 的梯度方向进行搜索,直到收敛到最优解。
- 共轭梯度法
共轭梯度法是一种改进后的梯度下降法。该方法的基本思想是,在当前点 ( x k , y k ) (x_k, y_k) (xk,yk) 处,沿着函数 f ( x ) f(x) f(x) 的梯度方向进行搜索,但在每次搜索时,要考虑上一次搜索的方向。
- 牛顿法
牛顿法是一种基于函数的二阶导数的迭代方法。该方法的基本思想是,在当前点 ( x k , y k ) (x_k, y_k) (xk,yk) 处,沿着函数 f ( x ) f(x) f(x) 的二阶导数矩阵的逆矩阵的方向进行搜索。
- 模拟退火法
模拟退火法是一种基于模拟物理现象的迭代方法。该方法的基本思想是,从初始点开始,通过逐步降低温度来搜索最优解。
结语
最优化问题是数学优化领域的一个重要问题。最优化算法有很多种,每种算法都有其优缺点。在实际应用中,需要根据具体的问题选择合适的算法。
补充说明
- 最优化问题的求解可以分为以下几个步骤:
- 确定目标函数。
- 确定约束条件。
- 选择合适的算法。
- 实现算法。
- 评估算法性能。
例如,以下代码块表示了一个二维函数的梯度下降法脚本:
def gradient_descent(f, x0, eps):
"""
梯度下降法求解多维函数的最优解。
Args:
f: 目标函数。
x0: 初始点。
eps: 精度。
Returns:
最优解。
"""
x = x0
while True:
dx = -grad(f, x)
x = x + dx
if np.linalg.norm(dx) < eps:
break
return x
以下表格表示了常用的多维函数求解方法的优缺点:
| 方法 | 优点 | 缺点 |
|---|---|---|
| 梯度下降法 | 简单易用 | 容易陷入局部最优解 |
| 共轭梯度法 | 收敛速度快 | 对初始值敏感 |
| 牛顿法 | 收敛速度最快 | 计算量大 |
| 拟牛顿法 | 收敛速度快,对初始值不敏感 | 对函数的二阶导数敏感 |
| 模拟退火法 | 适用于多峰函数,不易陷入局部最优解 | 收敛速度慢 |
| 遗传算法 | 适用于复杂的搜索空间,不易陷入局部最优解 | 收敛速度慢,对初始值敏感 |
| 粒子群算法 | 收敛速度快,不易陷入局部最优解 | 对初始值敏感 |
| 蝙蝠算法 | 收敛速度快,不易陷入局部最优解 | 对初始值敏感 |
| 蚁群算法 | 适用于具有结构的搜索空间,不易陷入局部最优解 | 收敛速度慢,对初始值敏感 |
| 蜂群算法 | 适用于具有结构的搜索空间,不易陷入局部最优解 | 收敛速度慢,对初始值敏感 |



![[ 蓝桥杯Web真题 ]-冬奥大抽奖](https://img-blog.csdnimg.cn/direct/b1d4a220f7ef485c85f9daf669335ec5.png)

![[GPT]Andrej Karpathy微软Build大会GPT演讲(上)--GPT如何训练](https://img-blog.csdnimg.cn/direct/7a4a51ddd529497c875a511e80f6b415.png)