给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
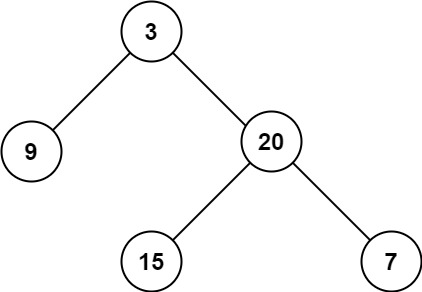
输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
输入:root = [1,null,2] 输出:2
递归法
本题可以使用前序(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,使用后序求的是高度。
-
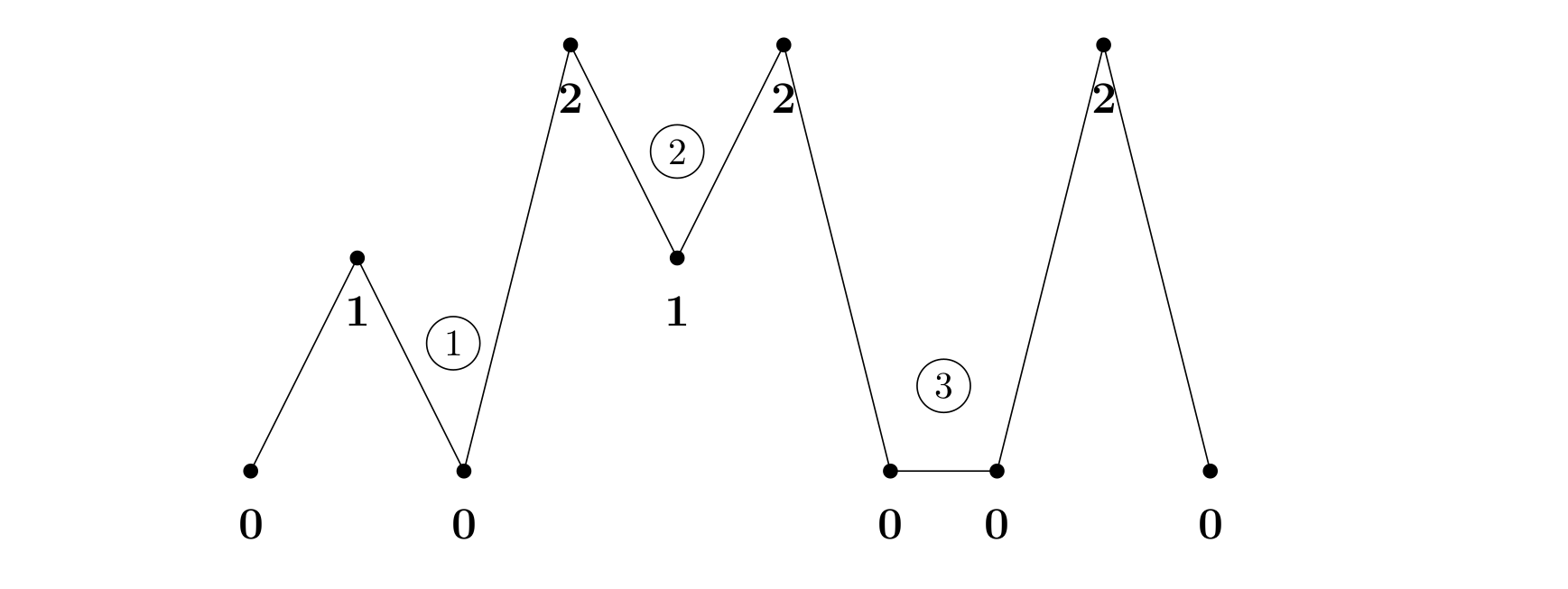
二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
-
二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数或者节点数(取决于高度从0开始还是从1开始)
而根节点的高度就是二叉树的最大深度,所以本题中我们通过后序求的根节点高度来求二叉树最大深度。
我先用后序遍历(左右中)来计算树的高度。
确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
代码如下:
int getDepth(TreeNode root)确定终止条件:如果为空节点的话,就返回0,表示高度为0。
代码如下:
if(root==null) return 0;确定单层递归的逻辑:先求它的左子树的深度,再求右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
代码如下:
int leftDepth=getDepth(root.left);//左
int rightDepth=getDepth(root.right);//右
int depth=1+Math.max(leftDepth,rightDepth);//中
return depth;
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
return getDepth(root);
}
int getDepth(TreeNode root){
if(root==null) return 0;
int leftDepth=getDepth(root.left);
int rightDepth=getDepth(root.right);
int depth=1+Math.max(leftDepth,rightDepth);
return depth;
}
}使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
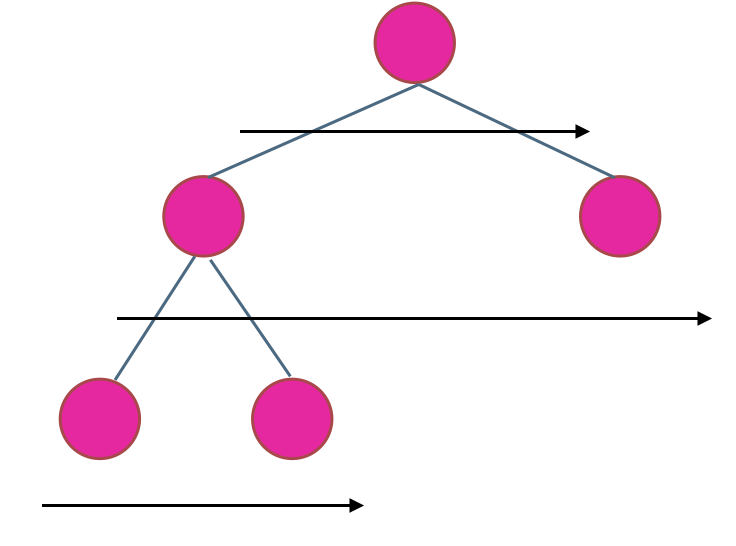
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
class Solution {
public int maxDepth(TreeNode root) {
if(root==null) return 0;
int depth=0;
Queue<TreeNode> queue=new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
depth++;
for(int i=0;i<size;i++){
TreeNode cur=queue.poll();
if(cur.left!=null) queue.add(cur.left);
if(cur.right!=null) queue.add(cur.right);
}
}
return depth;
}
}