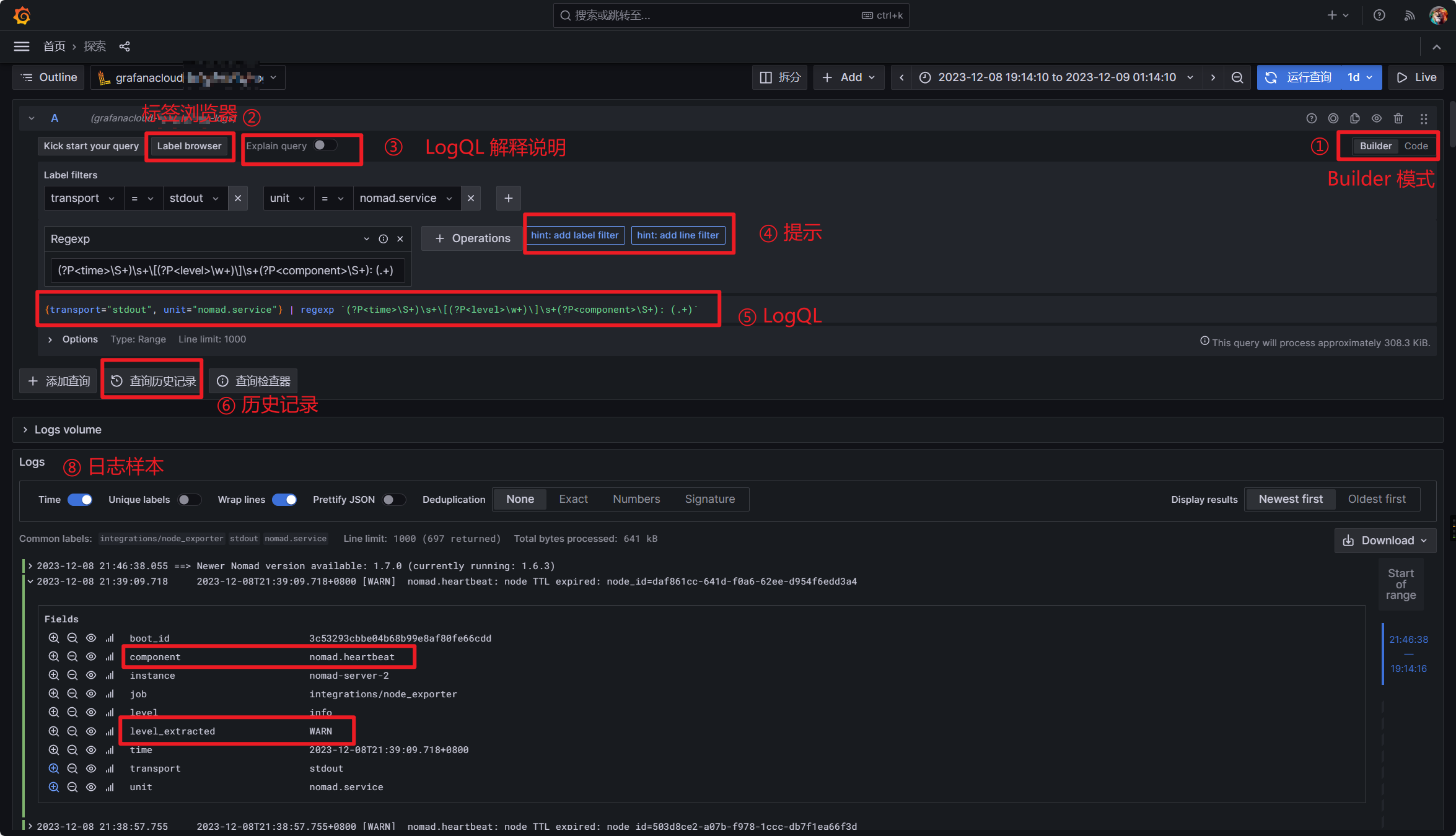
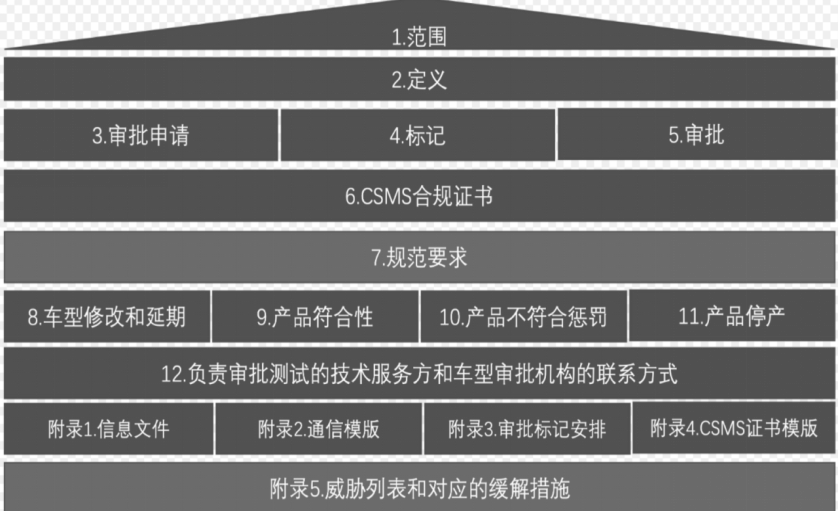
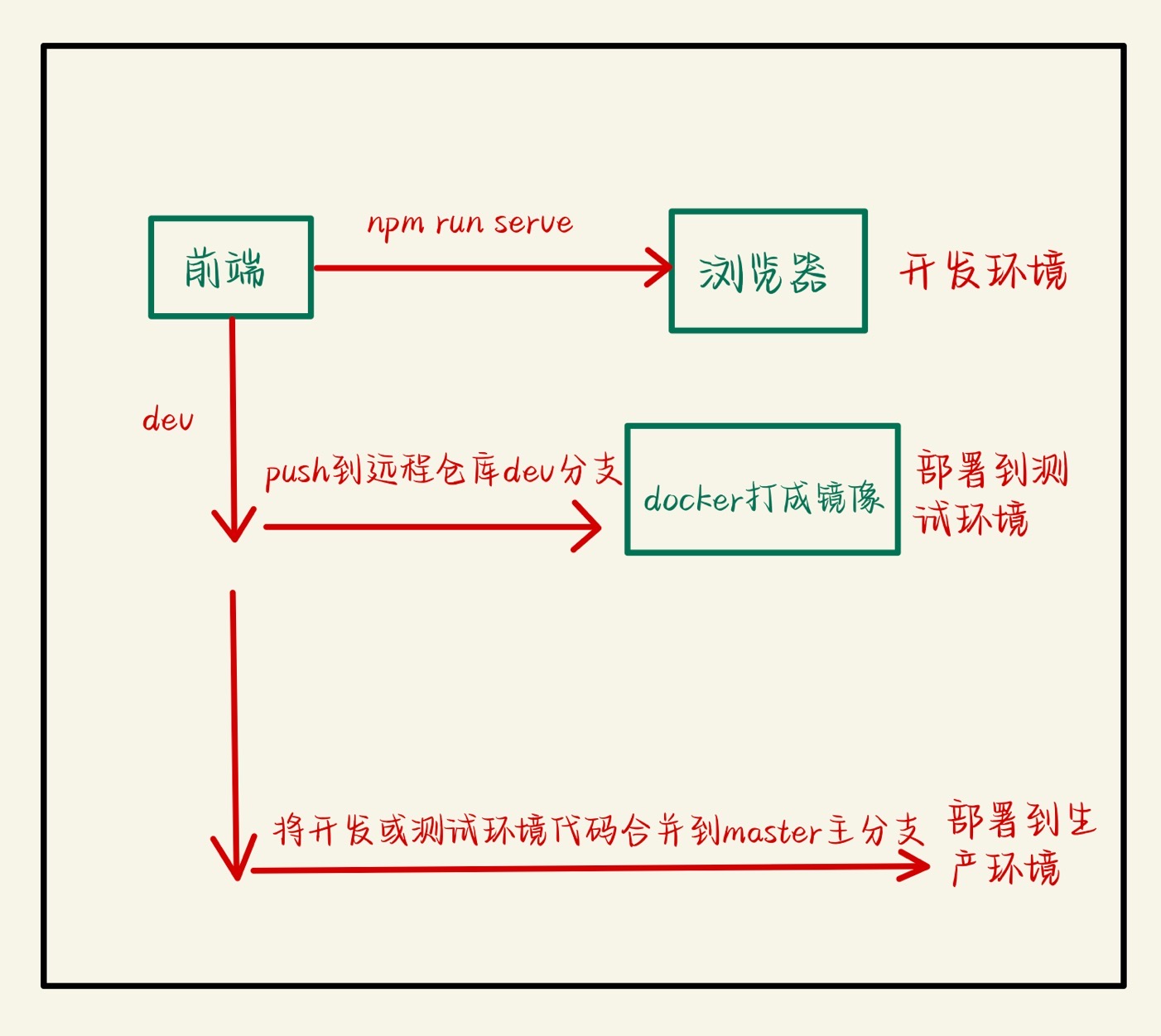
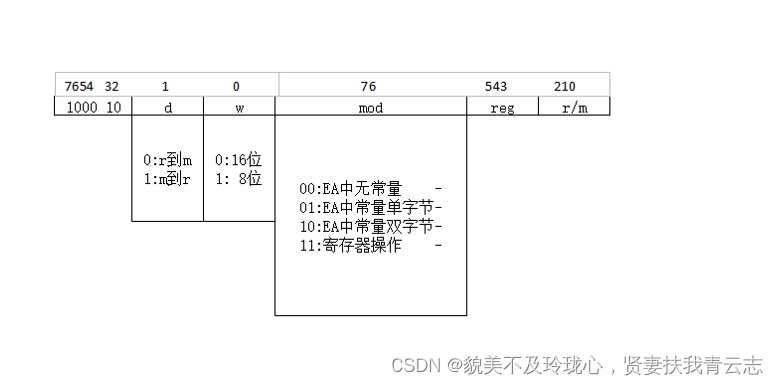
1、符合规定的三角剖分
1.1、定义
如果三角形的任何面的外接圆在其内部不包含顶点,则该三角形是 Delaunay 三角形。 约束 Delaunay 三角形是一种尽可能接近 Delaunay 的约束三角形。 约束 Delaunay 三角形的任何面的外接圆在其内部不包含从该面可见的数据点。
如果一条边内接于一个空圆(其内部不包含数据点),则该边被称为德劳内边。如果这条边的直径圆是空的,则该边被称为加布里埃尔边。
如果每个约束边都是一个Delaunay边,则称约束Delaunay三角剖分是保形的Delaunay三角剖分。由于约束Delaunay三角剖分中的任何边要么是Delaunay边,要么是约束边,因此保形的Delaunay三角剖分实际上是一个Delaunay三角剖分。唯一的区别是其中一些边被标记为约束边。
如果每个约束边都是加布里埃尔边,则受约束的德劳内三角网被称为一致的加布里埃尔三角网。 加布里埃尔属性比德劳内属性更强,每个加布里埃尔边都是德劳内边。 因此,一致的加布里埃尔三角网也是一致的德劳内三角网。
任何受约束的Delaunay三角剖分都可以通过在受约束的边上添加称为Steiner顶点的顶点,将其细化为一致的Delaunay三角剖分或一致的Gabriel三角剖分,直到它们被分解为足够小的子约束,成为Delaunay或Gabriel边。
1.2、构建符合规定的三角剖分
约束Delaunay三角剖分可以通过以下两个全局函数细化为符合规定的三角剖分:
template<class CDT>
void make_conforming_Delaunay_2 (CDT& t)
template<class CDT>
void make_conforming_Gabriel_2 (CDT& t)在这两种情况下,模板参数CDT必须由受约束的Delaunay三角剖分类实例化(参见第2章“三角剖分”)。
用于实例化参数CDT的约束Delaunay三角剖分的几何特征必须是概念ConformingDelaunayTriangulationTraits_2的模型。
受约束的Delaunay三角剖分t通过引用传递,并通过添加顶点细化为符合规定的Delaunay三角剖分或符合规定的Gabriel三角剖分。建议用户在原始三角剖分必须保留用于其他计算的情况下,对输入三角剖分进行复制。
make_conforming_Delaunay_2() 和 make_conforming_Gabriel_2() 使用的算法构建了内部数据结构,如果连续调用这两个函数,则需要对这些数据结构进行两次计算。为了避免这些数据被构造两次,高级用户可以使用 Triangulation_conformer_2<CDT> 类将约束 Delaunay 三角网细分为符合 Delaunay 三角网,然后再细分为符合 Gabriel 三角网。为了对细化算法进行额外控制,该类还提供了单独的函数,一次插入一个 Steiner 点。
1.3、范例
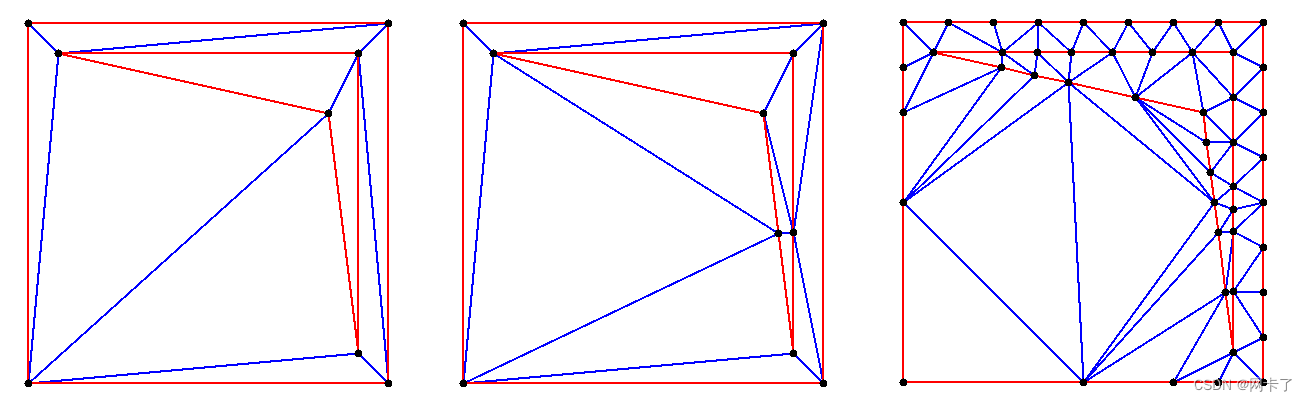
从左到右:初始Delaunay三角剖分、相应的一致Delaunay和相应的Gabriel三角剖分。
2、网格
2.1、定义
网格是将给定区域划分为形状和大小满足若干标准的单形。
域是用户想要网格化的区域。它必须是平面的有界区域。域由平面直线图定义,简称为Pslg,它是一组线段,其中两条线段要么不相交,要么共享一个端点。Pslg的线段是约束,将由网格中的边集表示。Pslg还可以包含孤立点,这些孤立点将作为网格的顶点出现。
Pslg的段可以是边界段或内部约束段。Pslg的段必须覆盖域的边界。
Pslg将平面划分为几个连通分量。默认情况下,域是有界连通分量的并集。
下图显示了不使用种子点定义的域的示例及其可能的网格。
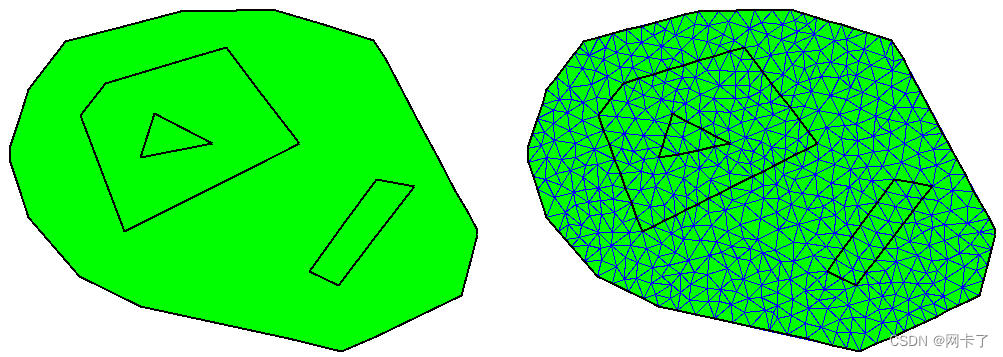
定义的域没有种子点和生成的网格。
用户可以通过提供一组种子点来覆盖此默认值。种子点标记要网格化的组件,或者标记不要网格化(孔)的组件。
关于用相同的Pslg和用于定义孔的两个种子点定义的另一个域,请参见下图。在相应的网格中,这两个孔是三角形的,但不是网格。
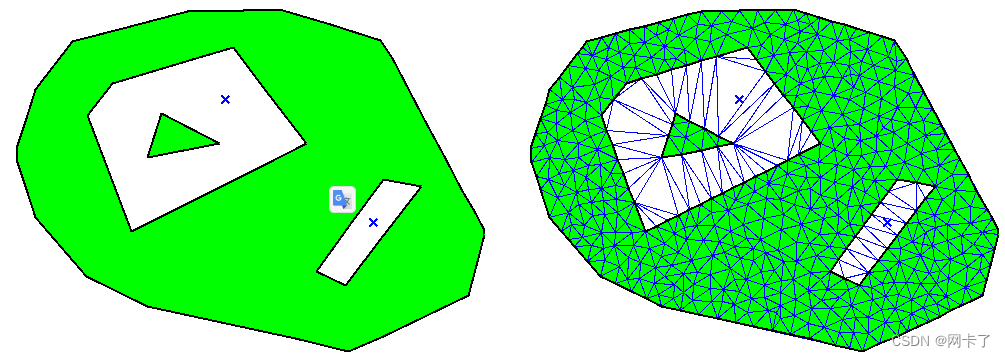
具有两个种子点的域,定义孔和生成的网格。
2.2、形状和尺寸标准
三角形形状标准是圆半径与最短边长之比的下界B。这样的界意味着三角形最小角度的下界为arcsin(1/2)B,最大角度的上界为π-2*arcsin(1/2)B。不幸的是,只有当B≥2√时,算法的终止才有保证,这对应于角度的下界为20.7度。
大小标准可以是任何倾向于偏好小三角形的标准。例如,大小标准可以是三角形最长边的长度的上限,或者外接圆半径的上限。大小限制可以在域中变化。例如,对于与给定线相交的三角形,大小标准可以规定一个较小的尺寸。
这两种类型标准都定义在对象criteria中,并作为参数传递给网格化函数。
2.3、网格剖分算法
网格问题的输入是一个Pslg和一组描述要网格化的域的种子,以及一组尺寸和形状标准。此包中实现的算法从输入Pslg的约束Delaunay三角划分开始,并使用Delaunay细化方法生成网格。此方法将新顶点插入三角划分中,尽可能远离其他顶点,并在满足标准时停止。
如果输入Pslg的入射段之间的所有角度都大于60度,并且如果圆周率/边比的界限大于2√,则该算法保证终止于满足尺寸和形状标准的网格。
如果某些输入角度小于 60 度,算法最终将得到一个网格,其中一些三角形在小输入角度附近违反了标准。这是不可避免的,因为输入段形成的小角度无法被抑制。此外,已经证明,某些具有小输入角度的域不能以甚至小于小输入角度的角度进行网格划分。请注意,如果域是多边形区域,则生成的网格将满足除小输入角度之外的大小和形状标准。此外,该算法可能成功地产生角度下限大于 20.7 度的网格,但没有任何保证。
2.4、构建网格
template<class CDT, class NamedParameters>
void refine_Delaunay_mesh_2 (CDT &t, NamedParameters np)模板参数CDT必须由受约束的Delaunay三角剖分类实例化。
CDT 的几何特征类必须是概念 DelaunayMeshTraits_2 的模型。这个概念通过添加几何谓词和构造函数来细化概念 ConformingDelaunayTriangulationTraits_2。
第二个模板参数 NamedParameters 允许传递一系列种子点来定义域。它还允许传递三角形必须满足的网格化标准。该标准必须是 MeshingCriteria_2 的模型。
CGAL为这个概念提供了两个模型:
Delaunay_mesh_criteria_2<CDT>,定义了一个形状标准,限制三角形的最小角度,
Delaunay_mesh_size_criteria_2<CDT>,它为前面的标准添加了一个最大边长度的限制。
如果使用不同的标准对同一个三角网格调用函数 refine_Delaunay_mesh_2() 多次,则算法会在每次调用时重建用于网格化的内部数据结构。为了避免每次调用时重建数据结构,高级用户可以使用类 Delaunay_mesher_2<CDT>。这个类还提供了逐步函数。这些函数一次插入一个顶点。
Delaunay_mesher_2<CDT> 类型的任何对象都是从对 CDT 的引用构造的,并且具有几个成员函数来定义要网格化的域并对 CDT 进行网格化。有关详细信息,请参见下面给出的示例和参考手册。请注意,在 Delaunay_mesher_2<CDT> 对象的生存期内,不应从外部修改 CDT。
一旦构建了网格,就可以使用面类型的 is_in_domain() 成员函数来确定三角剖分中的哪些面位于网格域中。
2.5、Lloyd法优化网格
该包还提供了一个全局函数,用于在Delaunay精化生成的网格上运行Lloyd优化迭代。这种网格优化的目标是改善网格内部的角度,并使其尽可能接近60度。
template< class CDT >
Mesh_optimization_return_code lloyd_optimize_mesh_2(CDT& cdt);请注意,此全局函数有几个命名参数来调整优化过程。
该优化过程交替地将顶点重新定位到其Voronoi单元的质心,并更新三角剖分的Delaunay连通性。质心是根据一个尺寸函数计算的,该函数旨在保持Delaunay细化生成的网格中点的局部密度。
下图,这是由refine_Delaunay_mesh_2()生成并使用lloyd_optimize_mesh_2()优化的网格。下图显示了这些网格内角度的直方图。

(左)由refine_Delanay_mesh2()生成的网格,用于统一大小调整标准。(右)显示了Lloyd优化100次迭代后的相同网格。
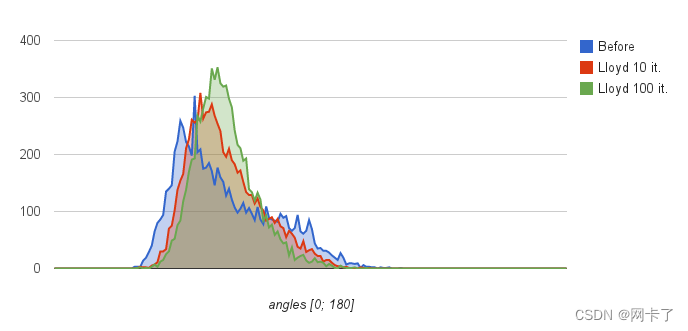
Delaunay细化后以及Lloyd优化的10次和100次迭代后网格内部角度的直方图。Delaunay精化后,角度在[28.5;121.9]度的区间内。经过10次Lloyd优化迭代后,它们处于[29.1;110.8]。100次迭代使它们达到[29.3;109.9]。
3、输入\输出
可以使用函数 ATTRIBUTE::IO::write_VTU()导出VTU中的网格结果。有关此格式的更多信息,请参阅VTK(VTU / VTP)文件格式。