题目一
小虎去买苹果,商店只提供两种类型的塑料袋,每种类型都有任意数量。1)能装下6个苹果的袋子2)能装下8个苹果的袋子小虎可以自由使用两种袋子来装苹果,但是小虎有强迫症,他要求自己使用的袋子数量必须最少,且使用的每个袋子必须装满。给定一个正整数N,返回至少使用多少袋子。如果N无法让使用的每个袋子必须装满,返回-1
先想一个暴力解:
1)如果苹果数小于0则直接返回-1
2)先给6号袋定义一个初始值
3)给八号袋装满看最多需要多少个八号袋子
3)然后求余下多少个看能否被6号袋子搞定如果能就得到答案
4)如果不能被6号袋子,则需要八号袋子少一个rest加8个
从而写出如下代码:
public static int minBags(int apple) {
if (apple < 0) {
return -1;
}
int bag8 = (apple >> 3);
int rest = apple - (bag8 << 3);
while(bag8 >= 0) {
// rest 个
if(rest % 6 ==0) {
return bag8 + (rest / 6);
} else {
bag8--;
rest += 8;
}
}
return -1;
}
public static void main(String[] args) {
for(int apple = 1; apple < 200;apple++) {
System.out.println(apple + " : "+ minBags(apple));
}
}
将如上代码跑一下得到如图控制台输出:
1 : -1
2 : -1
3 : -1
4 : -1
5 : -1
6 : 1
7 : -1
8 : 1
9 : -1
10 : -1
11 : -1
12 : 2
13 : -1
14 : 2
15 : -1
16 : 2
17 : -1
18 : 3
19 : -1
20 : 3
21 : -1
22 : 3
23 : -1
24 : 3
25 : -1
26 : 4
27 : -1
28 : 4
29 : -1
30 : 4
31 : -1
32 : 4
33 : -1
34 : 5
35 : -1
36 : 5
37 : -1
38 : 5
39 : -1
40 : 5
41 : -1
42 : 6
43 : -1
44 : 6
45 : -1
46 : 6
47 : -1
48 : 6
49 : -1
50 : 7
51 : -1
52 : 7
53 : -1
54 : 7
55 : -1
56 : 7
57 : -1
58 : 8
59 : -1
60 : 8
61 : -1
62 : 8
63 : -1
64 : 8
65 : -1
66 : 9
67 : -1
68 : 9
69 : -1
70 : 9
71 : -1
72 : 9
73 : -1
74 : 10
75 : -1
76 : 10
77 : -1
78 : 10
79 : -1
80 : 10
81 : -1
82 : 11
83 : -1
84 : 11
85 : -1
86 : 11
87 : -1
88 : 11
89 : -1
90 : 12
91 : -1
92 : 12
93 : -1
94 : 12
95 : -1
96 : 12
97 : -1
98 : 13
99 : -1
100 : 13
101 : -1
102 : 13
103 : -1
104 : 13
105 : -1
106 : 14
107 : -1
108 : 14
109 : -1
110 : 14
111 : -1
112 : 14
113 : -1
114 : 15
115 : -1
116 : 15
117 : -1
118 : 15
119 : -1
120 : 15
121 : -1
122 : 16
123 : -1
124 : 16
125 : -1
126 : 16
127 : -1
128 : 16
129 : -1
130 : 17
131 : -1
132 : 17
133 : -1
134 : 17
135 : -1
136 : 17
137 : -1
138 : 18
139 : -1
140 : 18
141 : -1
142 : 18
143 : -1
144 : 18
145 : -1
146 : 19
147 : -1
148 : 19
149 : -1
150 : 19
151 : -1
152 : 19
153 : -1
154 : 20
155 : -1
156 : 20
157 : -1
158 : 20
159 : -1
160 : 20
161 : -1
162 : 21
163 : -1
164 : 21
165 : -1
166 : 21
167 : -1
168 : 21
169 : -1
170 : 22
171 : -1
172 : 22
173 : -1
174 : 22
175 : -1
176 : 22
177 : -1
178 : 23
179 : -1
180 : 23
181 : -1
182 : 23
183 : -1
184 : 23
185 : -1
186 : 24
187 : -1
188 : 24
189 : -1
190 : 24
191 : -1
192 : 24
193 : -1
194 : 25
195 : -1
196 : 25
197 : -1
198 : 25
199 : -1
Process finished with exit code 0
发现从18-25偶数返回3,奇数返回-1
从26-33,偶数返回4,奇数返回-1
从34-41 偶数返回5,奇数返回-1
假设
18-25是第0组 -> 0+3
26-33是第1组- > 1+3
依次类推最终可得如下代码:
O(1)的时间复杂度解决
public static int minBagAwesome(int apple) {
if ((apple & 1) != 0) { // 如果是奇数,返回-1
return -1;
}
if (apple < 18) {
return apple == 0 ? 0 : (apple == 6 || apple == 8) ? 1
: (apple == 12 || apple == 14 || apple == 16) ? 2 : -1;
}
return (apple - 18) / 8 + 3;
}
题目二
给定一个正整数N,表示有N份青草统一堆放在仓库里有一只牛和一只羊,牛先吃,羊后吃,它俩轮流吃草不管是牛还是羊,每一轮能吃的草量必须是:1,4,16,64…(4的某次方)谁最先把草吃完,谁获胜假设牛和羊都绝顶聪明,都想赢,都会做出理性的决定根据唯一的参数N,返回谁会赢
这道题在博弈论的视角下是无选择的,先手一定会考虑一定能赢的情况,后手也不会失误
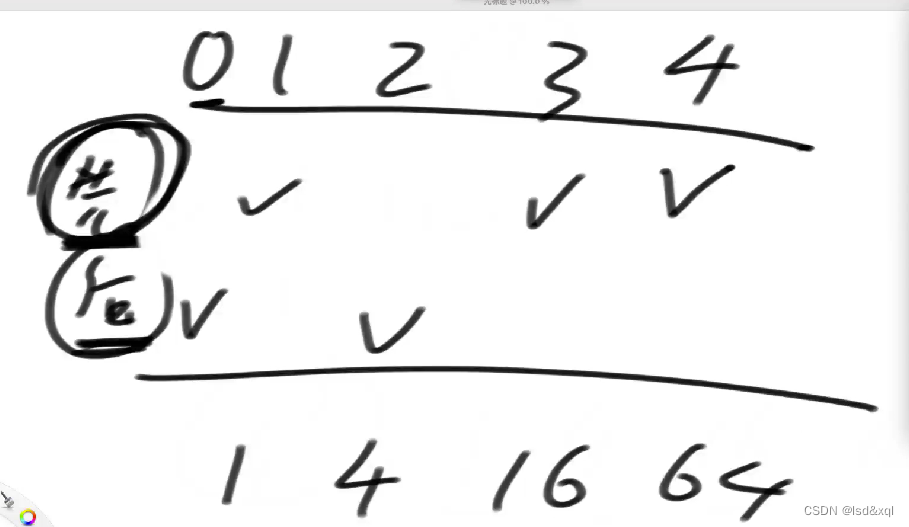
前四分份草的结果。
可以写如下代码:
// 如果n份草,最终先手赢,返回"先手"
// 如果n份草,最终后手赢,返回"后手"
public static String whoWin(int n) {
//先写hardCode
if (n < 5) {
//0或2的时候后手赢
return n == 0 || n == 2 ? "后手" : "先手";
}
// 进到这个过程里来,当前的先手,先选(和全局的先手无关)
int want = 1;
while (want <= n) {
//如果后续的过程种,当前这个过程的先手赢了
if (whoWin(n - want).equals("后手")) {
return "先手";
}
//防止want溢出,如果want小于等于n/4那么want乘以4一定安全
if (want <= (n / 4)) {
want *= 4;
} else {
break;
}
}
return "后手";
}
public static void main(String[] args) {
for (int i = 0; i <= 50; i++) {
System.out.println(i + " : " + whoWin(i));
}
}
发现按照后先后先先的规律出现
0 : 后手
1 : 先手
2 : 后手
3 : 先手
4 : 先手
5 : 后手
6 : 先手
7 : 后手
8 : 先手
9 : 先手
10 : 后手
11 : 先手
12 : 后手
13 : 先手
14 : 先手
15 : 后手
16 : 先手
17 : 后手
18 : 先手
19 : 先手
20 : 后手
21 : 先手
22 : 后手
23 : 先手
24 : 先手
25 : 后手
26 : 先手
27 : 后手
28 : 先手
29 : 先手
30 : 后手
31 : 先手
32 : 后手
33 : 先手
34 : 先手
35 : 后手
36 : 先手
37 : 后手
38 : 先手
39 : 先手
40 : 后手
41 : 先手
42 : 后手
43 : 先手
44 : 先手
45 : 后手
46 : 先手
47 : 后手
48 : 先手
49 : 先手
50 : 后手
Process finished with exit code 0
根据上面得出的结论可以推导出如下代码:
public static String winner2(int n) {
if (n % 5 == 0 || n % 5 == 2) {
return "后手";
} else {
return "先手";
}
}
题目三
定义一种数:可以表示成若干(数量>1)连续正数和的数 比如: 5 = 2+3,5就是这样的数 12 = 3+4+5,12就是这样的数 1不是这样的数,因为要求数量大于1个、连续正数和 2 = 1 + 1,2也不是,因为等号右边不是连续正数 给定一个参数N,返回是不是可以表示成若干连续正数和的数
暴力:
一个n看能否被1开头的连续数搞出来
1个n看能否被2开头的连续数搞出来
依次递推。
写出如下代码:
public static boolean isMSum1(int num) {
//从某个数开始一直加加到某一个数小于num,某一个数的下一个数加上大于num
//则表示以当前数开始的连续和不能组成num
for (int start = 1; start <= num; start++) {
int sum = start;
for (int j = start + 1; j <= num; j++) {
if (sum + j > num) {
break;
}
if (sum + j == num) {
return true;
}
sum += j;
}
}
return false;
}
public static void main(String[] args) {
for (int num = 1; num < 200; num++) {
System.out.println(num + " : " + isMSum1(num));
}
}
得到:
1 : false
2 : false
3 : true
4 : false
5 : true
6 : true
7 : true
8 : false
9 : true
10 : true
11 : true
12 : true
13 : true
14 : true
15 : true
16 : false
17 : true
18 : true
19 : true
20 : true
21 : true
22 : true
23 : true
24 : true
25 : true
26 : true
27 : true
28 : true
29 : true
30 : true
31 : true
32 : false
33 : true
34 : true
35 : true
36 : true
37 : true
38 : true
39 : true
40 : true
41 : true
42 : true
43 : true
44 : true
45 : true
46 : true
47 : true
48 : true
49 : true
50 : true
51 : true
52 : true
53 : true
54 : true
55 : true
56 : true
57 : true
58 : true
59 : true
60 : true
61 : true
62 : true
63 : true
64 : false
65 : true
66 : true
67 : true
68 : true
69 : true
70 : true
71 : true
72 : true
73 : true
74 : true
75 : true
76 : true
77 : true
78 : true
79 : true
80 : true
81 : true
82 : true
83 : true
84 : true
85 : true
86 : true
87 : true
88 : true
89 : true
90 : true
91 : true
92 : true
93 : true
94 : true
95 : true
96 : true
97 : true
98 : true
99 : true
100 : true
101 : true
102 : true
103 : true
104 : true
105 : true
106 : true
107 : true
108 : true
109 : true
110 : true
111 : true
112 : true
113 : true
114 : true
115 : true
116 : true
117 : true
118 : true
119 : true
120 : true
121 : true
122 : true
123 : true
124 : true
125 : true
126 : true
127 : true
128 : false
129 : true
130 : true
131 : true
132 : true
133 : true
134 : true
135 : true
136 : true
137 : true
138 : true
139 : true
140 : true
141 : true
142 : true
143 : true
144 : true
145 : true
146 : true
147 : true
148 : true
149 : true
150 : true
151 : true
152 : true
153 : true
154 : true
155 : true
156 : true
157 : true
158 : true
159 : true
160 : true
161 : true
162 : true
163 : true
164 : true
165 : true
166 : true
167 : true
168 : true
169 : true
170 : true
171 : true
172 : true
173 : true
174 : true
175 : true
176 : true
177 : true
178 : true
179 : true
180 : true
181 : true
182 : true
183 : true
184 : true
185 : true
186 : true
187 : true
188 : true
189 : true
190 : true
191 : true
192 : true
193 : true
194 : true
195 : true
196 : true
197 : true
198 : true
199 : true
发现只要是2的某次方那么这个数就返回false,那么只需要判断某个数的二进制是否只有一个1即可,将某个数的最右侧的1取出来和它自己比较如果相等则是2的n次方
num&(~num+1)
public static boolean isMSum2(int num) {
// return num == (num & (~num + 1));
//
// return num == (num & (-num));
return (num & (num - 1)) != 0;
}
public static void main(String[] args) {
for (int num = 1; num < 200; num++) {
System.out.println(num + " : " + isMSum1(num));
}
System.out.println("test begin");
for (int num = 1; num < 5000; num++) {
if (isMSum1(num) != isMSum2(num)) {
System.out.println("Oops!");
}
}
System.out.println("test end");
}
总结
1)某个面试题,输入参数类型简单,并且只有一个实际参数2)要求的返回值类型也简单,并且只有一个
3)用暴力方法,把输入参数对应的返回值,打印出来看看,进而优化code
根据数据规模猜解法
1)C/C++,1秒处理的指令条数为10的8次方
2)Java等语言,1~4秒处理的指令条数为10的8次方、
3)这里就有大量的空间了!
题目五
int[] d,d[i]:i号怪兽的能力 int[]
p,p[i]:i号怪兽要求的钱
开始时你的能力是0,你的目标是从0号怪兽开始,通过所有的怪兽。 如果你当前的能力,小于i号怪兽的能力,你必须付出p[i]的钱,贿赂这个怪兽,然后怪兽就会加入你,他的能力直接累加到你的能力上;如果你当前的能力,大于等于i号怪兽的能力,你可以选择直接通过,你的能力并不会下降,你也可以选择贿赂这个怪兽,然后怪兽就会加入你,他的能力直接累加到你的能力上。 返回通过所有的怪兽,需要花的最小钱数。
递归解法:
// int[] d d[i]:i号怪兽的武力
// int[] p p[i]:i号怪兽要求的钱
// ability 当前你所具有的能力
// index 来到了第index个怪兽的面前
// 目前,你的能力是ability,你来到了index号怪兽的面前,如果要通过后续所有的怪兽,
// 请返回需要花的最少钱数
public static long process1(int[] d, int[] p, int ability, int index) {
if (index == d.length) {
return 0;
}
//必须要花钱的情况
if (ability < d[index]) {
//记录花的钱 当前能力加怪兽的能力,去打后面的怪兽
return p[index] + process1(d, p, ability + d[index], index + 1);
} else { // ability >= d[index] 可以贿赂,也可以不贿赂
return Math.min(
//花钱
p[index] + process1(d, p, ability + d[index], index + 1),
//不花钱
0 + process1(d, p, ability, index + 1));
}
}
public static long func1(int[] d, int[] p) {
return process1(d, p, 0, 0);
}
第二种解法:
先定义一张表i表示第i号怪兽,j表示所要花的钱数,从0号怪兽到i号怪兽我花的钱为多少的时候我的能力最大,并且要严格花费j元,如果没有严格花j元则为-1,并且我在0-i-1的位置上已花费了j元,那么我通过i-1位置对应的能力一定要大于i号怪兽的能力。
如dp[100][130],表示我想从0号怪兽通关到100号怪兽严格花费130元,假设100号怪兽能力是50,贿赂它的钱是30。
第一种情况:不想贿赂100号怪兽一定是0-99号怪兽贿赂花了130,如果dp[99][130] = -1,则dp[100][130]也是-1,如果dp[99][130]=80则可以直接通过的得到dp[100][130]为80的能力。
第二种情况:贿赂100号怪兽,假设当前怪兽能力为x,花的是y
要整体凑出j元
那么dp[i-1][j-y] 不等于 -1
// 从0....index号怪兽,花的钱,必须严格==money
// 如果通过不了,返回-1
// 如果可以通过,返回能通过情况下的最大能力值
public static long process2(int[] d, int[] p, int index, int money) {
if (index == -1) { // 一个怪兽也没遇到呢
return money == 0 ? 0 : -1;
}
// index >= 0
// 1) 不贿赂当前index号怪兽
long preMaxAbility = process2(d, p, index - 1, money);
long p1 = -1;
//如果之前的能力不为-1并且之前的能力大于等于当前的能力则记录一个p1
if (preMaxAbility != -1 && preMaxAbility >= d[index]) {
p1 = preMaxAbility;
}
// 2) 贿赂当前的怪兽 当前的钱 p[index]
long preMaxAbility2 = process2(d, p, index - 1, money - p[index]);
long p2 = -1;
if (preMaxAbility2 != -1) {
p2 = d[index] + preMaxAbility2;
}
return Math.max(p1, p2);
}
public static int minMoney2(int[] d, int[] p) {
int allMoney = 0;
for (int i = 0; i < p.length; i++) {
allMoney += p[i];
}
int N = d.length;
for (int money = 0; money < allMoney; money++) {
if (process2(d, p, N - 1, money) != -1) {
return money;
}
}
return allMoney;
}
public static long func3(int[] d, int[] p) {
int sum = 0;
for (int num : p) {
sum += num;
}
// dp[i][j]含义:
// 能经过0~i的怪兽,且花钱为j(花钱的严格等于j)时的武力值最大是多少?
// 如果dp[i][j]==-1,表示经过0~i的怪兽,花钱为j是无法通过的,或者之前的钱怎么组合也得不到正好为j的钱数
int[][] dp = new int[d.length][sum + 1];
for (int i = 0; i < dp.length; i++) {
for (int j = 0; j <= sum; j++) {
dp[i][j] = -1;
}
}
// 经过0~i的怪兽,花钱数一定为p[0],达到武力值d[0]的地步。其他第0行的状态一律是无效的
dp[0][p[0]] = d[0];
for (int i = 1; i < d.length; i++) {
for (int j = 0; j <= sum; j++) {
// 可能性一,为当前怪兽花钱
// 存在条件:
// j - p[i]要不越界,并且在钱数为j - p[i]时,要能通过0~i-1的怪兽,并且钱数组合是有效的。
if (j >= p[i] && dp[i - 1][j - p[i]] != -1) {
dp[i][j] = dp[i - 1][j - p[i]] + d[i];
}
// 可能性二,不为当前怪兽花钱
// 存在条件:
// 0~i-1怪兽在花钱为j的情况下,能保证通过当前i位置的怪兽
if (dp[i - 1][j] >= d[i]) {
// 两种可能性中,选武力值最大的
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);
}
}
}
int ans = 0;
// dp表最后一行上,dp[N-1][j]代表:
// 能经过0~N-1的怪兽,且花钱为j(花钱的严格等于j)时的武力值最大是多少?
// 那么最后一行上,最左侧的不为-1的列数(j),就是答案
for (int j = 0; j <= sum; j++) {
if (dp[d.length - 1][j] != -1) {
ans = j;
break;
}
}
return ans;
}
先定义1张表
dpp[i][j] 从0号怪兽通关到第i号怪兽我的能力要大于等于j至少要花多少钱
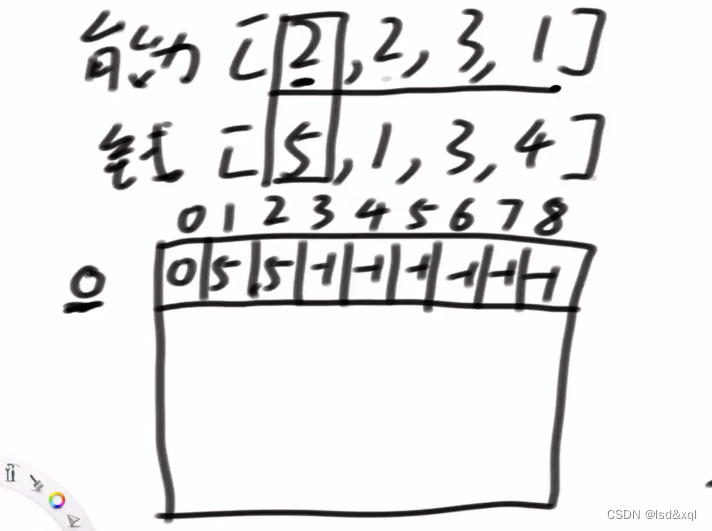
public static long func2(int[] d, int[] p) {
int sum = 0;
for (int num : d) {
sum += num;
}
long[][] dp = new long[d.length + 1][sum + 1];
for (int i = 0; i <= sum; i++) {
dp[0][i] = 0;
}
for (int cur = d.length - 1; cur >= 0; cur--) {
for (int hp = 0; hp <= sum; hp++) {
// 如果这种情况发生,那么这个hp必然是递归过程中不会出现的状态
// 既然动态规划是尝试过程的优化,尝试过程碰不到的状态,不必计算
if (hp + d[cur] > sum) {
continue;
}
if (hp < d[cur]) {
dp[cur][hp] = p[cur] + dp[cur + 1][hp + d[cur]];
} else {
dp[cur][hp] = Math.min(p[cur] + dp[cur + 1][hp + d[cur]], dp[cur + 1][hp]);
}
}
}
return dp[0][0];
}