##栈部分-（叠猫猫）

##抽象数据类型栈的定义：是一种遵循先入后出的逻辑的线性数据结构。

换种方式去理解这种数据结构如果我们在一摞盘子中取到下面的盘子，我们首先要把最上面的盘子依次拿走，才可以继续拿下面的盘子，我们把盘子替代成各种类型的元素（如整形，字符，对象等），对于栈就是类似这种衍生出来的线性数据结构。

##栈的定义（c++）：是限定仅在表尾进行插入或删除操作的线性表

##图例介绍

##LIFO结构：

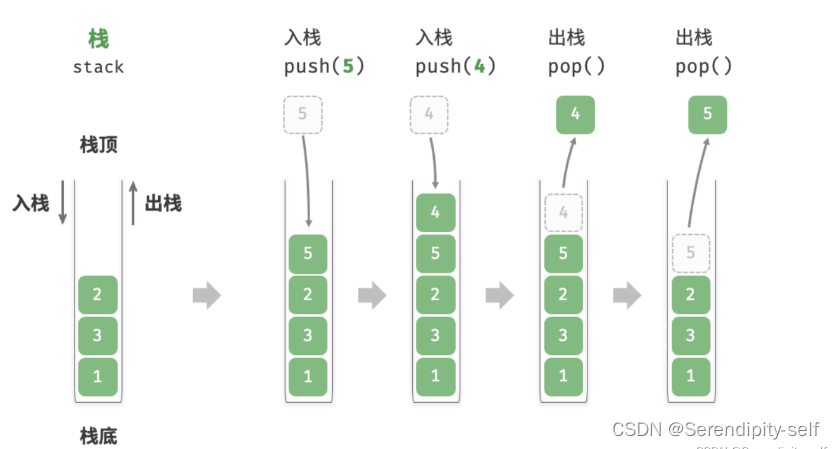
##动态过程

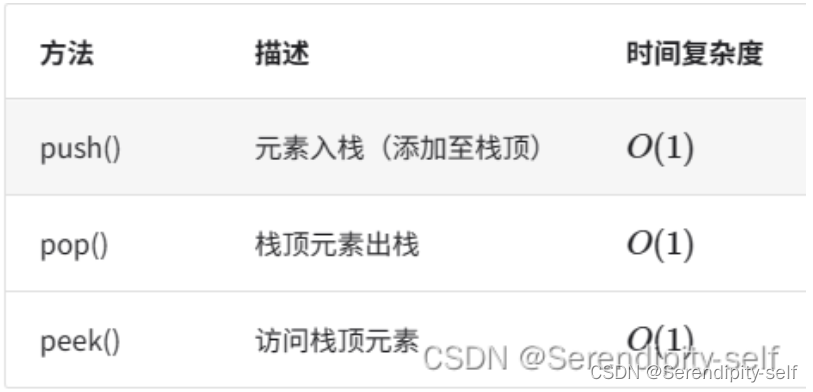
##栈的表示和实现

##栈常用操作：pop(),push(),peek()

然而，某些语言可能没有专门提供栈类，这时我们可以将该语言的“数组”或“链表”当作栈来使用，并在程序逻辑上忽略与栈无关的操作。

栈遵循先入后出的原则，我们只能在栈顶添加或删除元素。

但是，数组和链表都可以在任意位置添加和删除元素，所以栈可以看作是一种受限制的数组或链表。

##栈的顺序表示-基于数组的实现

采用具有一块连续存储的地址进行相关操作，具有代表性的便是数组，基于数组的实现栈。

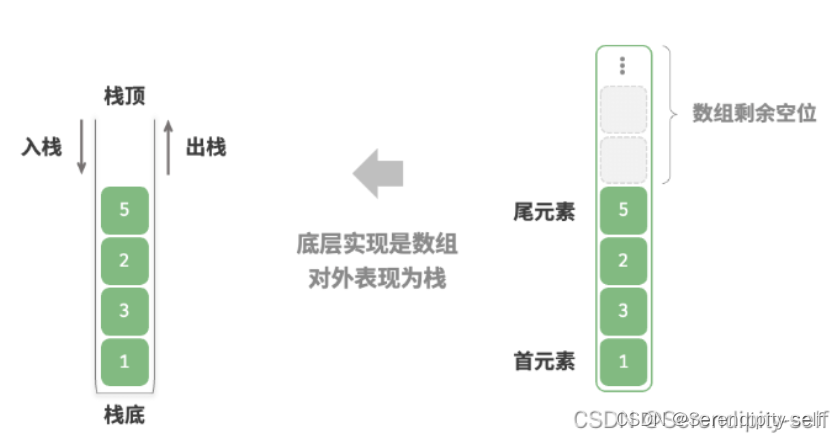
我们可以将数组的尾部视作栈顶，入栈和出栈操作分别对应在数组的尾部添加或者删除元素，时间复杂度都为O(1)。

##图解

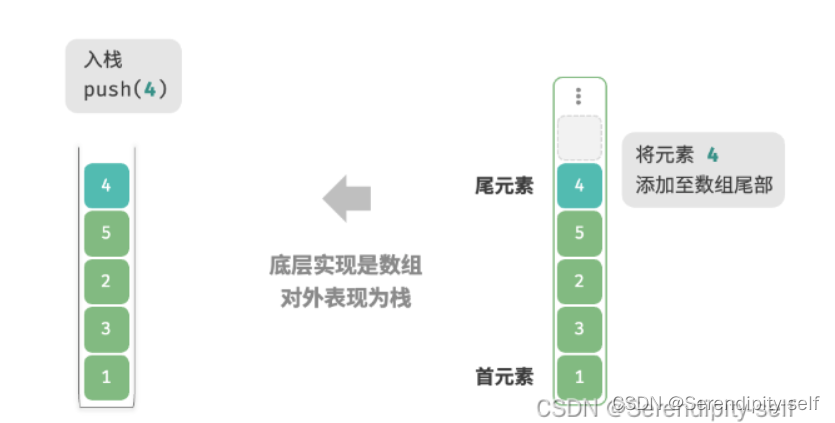
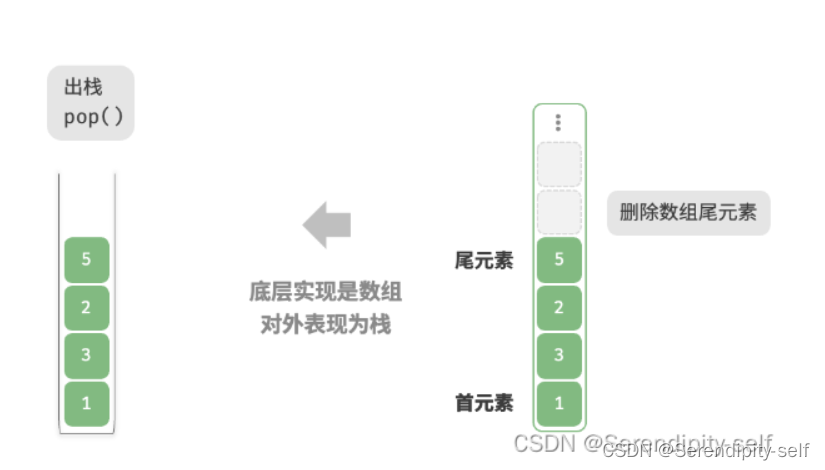
##python代码实现

考虑到入栈的元素可能会远远不断的地增加，因此我们可以使用动态数组，这样就可以不用自行处理数组的扩容问题。

class ArrayStack:
    """基于数组实现额栈"""

    def __init__(self):
        """构造方法"""
        self._stack:list[int] = []

    def size(self):
        """获取栈的长度"""
        return len(self._stack)

    def is_empty(self):
        """判断栈是否为空"""
        return self._stack == []

    def push(self,item):
        """入栈"""
        self._stack.append(item)

    def pop(self):
        """出栈"""
        if self.is_empty():
            raise IndexError("栈为空")
        return self._stack.pop()

    def peek(self):
        """访问栈顶元素"""
        if self.is_empty():
            raise IndexError("栈为空")
        return self._stack[-1]

    def to_list(self):
        """返回列表用于打印"""
        return self._stack

时间效率：在基于数组的实现中，入栈和出栈操作都在预先分配好的连续内存中进行，具有很好的缓存本地性，因此效率较高。然而，如果入栈时超出数组容量，会触发扩容机制，导致该次入栈操作的时间复杂度变为O(n) 。

空间效率：在初始化列表时，系统会为列表分配“初始容量”，该容量可能超出实际需求；并且，扩容机制通常是按照特定倍率（例如 2 倍）进行扩容的，扩容后的容量也可能超出实际需求。因此，基于数组实现的栈可能造成一定的空间浪费。