机器学习算法（9）——集成技术（Bagging—

机器学习算法（9）——集成技术（Bagging——随机森林分类器和回归）

news2024/11/17 4:49:16

一、说明

在这篇文章，我将向您解释集成技术和著名的集成技术之一，它属于装袋技术，称为随机森林分类器和回归。

集成技术是机器学习技术，它结合多个基本模块和模型来创建最佳预测模型。为了更好地理解这个定义，我们需要退一步考虑机器学习和模型构建的最终目标。一旦我们对此有了清晰的认识，我们就可以深入研究具体的例子以及首选集成模型的原因。在上一篇文章中，我们学习了决策树。

机器学习算法(8)——决策树算法

在本文中，我将重点讨论决策树的用途。决策树是最强大的之一......

向开发网

本文讨论使用决策树来确定个人是否应该在某些天气条件下在户外打高尔夫球。这棵树会考虑各种天气因素，并根据每个因素做出决定或提出另一个问题。例如，如果是阴天，则决定在外面玩，但如果是晴天、雨天或有风，树会在决定是否玩之前询问进一步的问题。

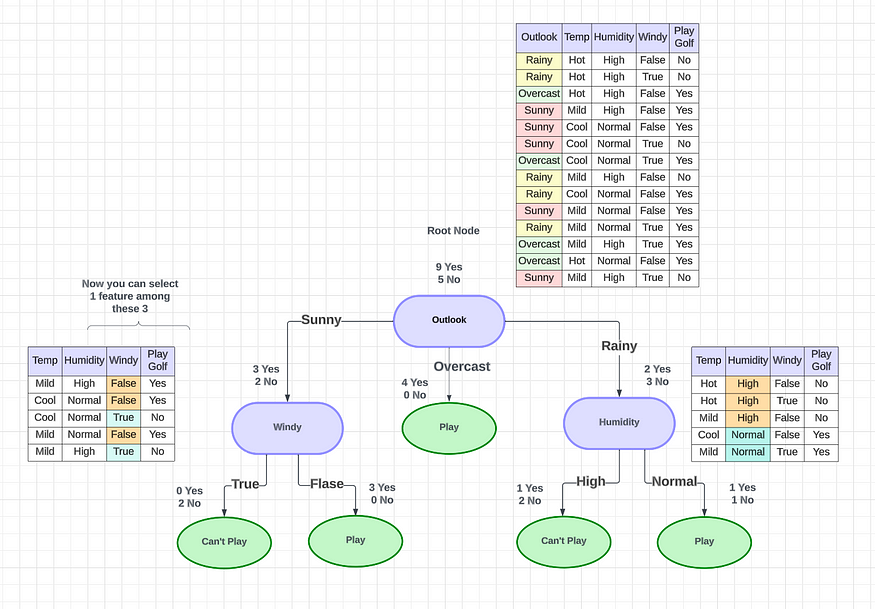
要创建决策树，我们必须考虑将使用哪些特征来做出决策，以及将使用什么阈值将每个问题分类为是或否答案。我们可以继续添加问题，直到定义是和否类。但如果我们想问自己是否有朋友可以一起玩，会发生什么呢？如果我们有朋友的话，我们每次都会玩。如果没有，我们可能会继续问自己有关天气的问题。通过添加一个附加问题，我们希望更好地定义“是”和“否”类。但我们怎样才能做到这一点呢？

这里需要用到集成技术。使用集成方法使我们能够考虑决策树样本，确定每次分割时使用哪些特征，并根据样本决策树的聚合结果做出最终预测器。这种方法比仅依靠一棵决策树来做出最终决策更可靠。在 Esemble 技术中，有 2 种技术。

套袋技术
升压技术

二、装袋技术如何发挥作用？

Bagging 也称为引导聚合，通过使用多个模型训练数据集来获得更准确的输出。这个主题特别重要，因为许多公司现在在数据分析中使用这些技术。

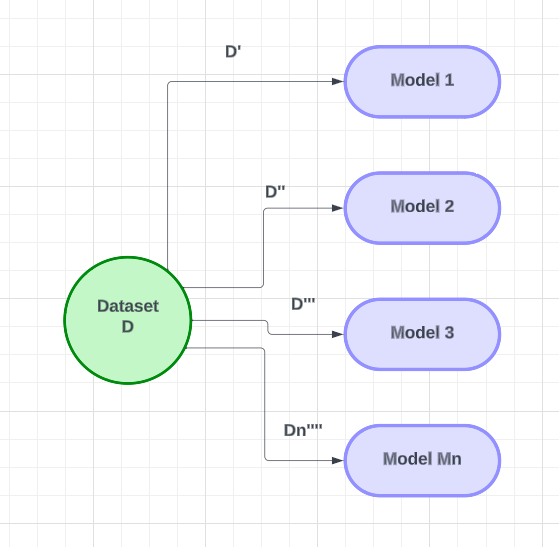
假设我们有一个特定的问题陈述，并且有一个名为 D 的数据集。在这个特定的数据集中，我们将创建几个基本模型（M1、M2、M3 …… Mn）并使用它们来创建基于多个的学习器。对于每个模型，我们将向M1 模型提供小于数据集中记录数（n）的数据集样本（D'）。我们将使用行采样和每个模型的替换来提供数据。对于下一个模型，我们将重复相同的过程，我们将重新采样记录并将其提供给模型。每个模型都会有一组不同的数据。在向模型提供数据后，他们将接受数据训练。将对组中的所有模型重复此过程。

完成训练后，我们将使用测试数据集中的新数据进行预测。对于二元分类，我们将“测试 D”数据发送到模型 1。如果模型1输出1，模型2输出0，模型3输出1，模型Mn输出1，我们将使用投票分类器来组合测试数据的模型的输出（为1）。获得多数票的输出将被考虑。通过使用带替换的行采样和投票分类器，我们将组合模型的输出以获得最终结果。这就是套袋技术的工作原理。

注意：对于回归问题，我们可以将输出均值作为最终结果。

在装袋技术中，我们使用两种算法，

随机森林分类器
随机森林回归

三、随机森林分类器和随机森林回归

自举随机森林算法将集成学习方法与决策树框架相结合，从数据中创建多个随机抽取的决策树，对结果进行平均以输出新结果，这通常会导致强大的预测/分类。

让我向您展示一些示例，以帮助您了解随机如何处理数据集。在bagging中，我们使用多个基学习器模型，例如决策树1、决策树2、决策树3……决策树Mn（这里我们将用4个模型来解释）。在随机森林中，我们使用决策树来设计这些模型。我们从给定的数据集中采样一些行和列。我们使用带替换的行采样，这意味着我们从数据集中取出一些行（ m ）并选择一些列（ d）作为特征样本。这就是我们如何使用 bagging 为决策树选择行子集。决策树中的记录数始终小于数据集中的记录数。

Number of Records                         : m*d
Number of Rows                            : d
Number of features(columns)               : m
Number of rows selected for row sampling  : d'
Number of features for feature sampling   : n

d' < d
n < m

这里我们有少量记录，因此我们指定其中一些用于训练。然后，我们对这些记录进行采样，并将它们提供给第一个决策树。对第二个决策树重复相同的过程，但使用替换采样。当我们进行替换采样时，并非所有记录都会重复 - 相反，会获取一个新样本并将其提供给第二个决策树。在此过程中，某些记录和特征可能会重复，但许多记录会发生变化。对于每个决策树重复此行和特征采样过程，每次使用不同的特征集。

行采样(RS)+特征采样(FS)

在给定数据上训练决策树后，它可以准确预测新测试数据的结果。在二元分类问题中，如果决策树给出正（1）输出，我们可以假设它是正（1）。为了做出最终预测，我们使用模型中的多数票。例如，如果模型 1、模型 2 和模型 4 假设输出为 1，则我们假设它为正。

当我们使用多个决策树时，我们需要考虑两个属性。

低偏差
高方差

如果我们创建一个完整深度的决策树，它将具有低偏差和高方差，并且它将根据我们的训练数据集进行适当的训练。所以训练误差会非常低。

当决策树由于新的测试数据而产生大量错误时，就会出现高方差。当决策树创建到其完整深度时，就会发生这种情况，称为过度拟合。在随机森林中，使用多个决策树，每个决策树都具有高方差。然而，当使用多数投票组合这些决策树时，高方差将转换为低方差。这是通过在数据集中使用行和特征采样来实现的。通过组合多个决策树的输出，可以降低高方差。

如果我们有 1000 条记录并更改 200 条记录，这将如何影响输出？

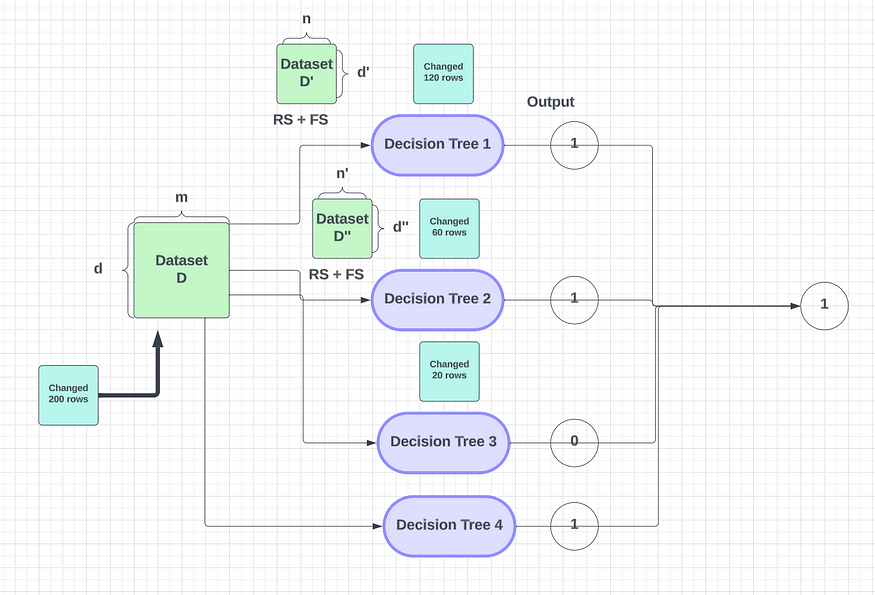
对输出的影响

我们目前正在对 200 条记录的每次决策树更改进行行和特征采样。这可确保 200 条记录在决策树之间正确划分。一些记录将进入决策树 2 或 1，但此更改不会显着影响决策树的准确性或输出。这是由于随机森林的高方差特性，它适用于大多数机器学习用例。如果这是一个回归问题，决策树将给出一个连续值，我们可以取所有输出的平均值或特定输出的中位数。

在随机森林中，特定输出的中值取决于输出的分布和决策树的结构。通常，随机森林的工作原理是查找所有决策树的输出平均值。然而，为了减少方差，我们使用多个决策树、行采样和特征采样。

随机森林既有分类器又有回归。它们之间的唯一区别是分类器使用多数投票，而回归器找到所有决策树输出的平均值或中值。通过调整超参数（例如决策树的数量），您可以优化随机森林的性能。

随机森林或决策树是否需要标准化（缩放）？

没有！