前言

今天是美好的一天，现在是体育课时间，我神奇的体育老师让我们男生需要做40个俯卧撑作为期末作业，可惜啊可惜，我差了一丝丝，这个东西对于我这种高瘦子还是有很大的挑战的，我现在能充分的感觉到码字的手已经不是那么的正常了，本人是热爱运动的，但是对于引体向上和俯卧撑这种运动我从事感到无可奈何，难！难！难！所以各位同学一定要加强锻炼哦！今天的这篇博客是比较特殊的一次，因为现在是北京时间：2022/12/30/17:06 ，可以看出现在不是凌晨，本来确实是想在凌晨的时候将这篇博客给产出的，但是怕因为困而影响了质量，所以我留到了现在来写。ok！我们现在就开始学习一下有关数据结构中的迷宫问题，我们从初阶的迷宫问题到进阶迷宫问题。

1.初阶迷宫题目

题目描述：定义一个二维数组N*M(其中2<=N<=10,2<=M<=10)，如下图所示：

 int maze[5][5] = { 0 1 0 0 0
                    0 1 1 1 0
                    0 0 0 0 0 
                    0 1 1 1 0
                    0 0 0 1 0
                   };

并且此时的这个二维数组表示的就是一个迷宫，其中1表示的是墙壁，0表示的是可以走的路，只能横着或者竖着走，不可以斜着走，要求编程找出从左上角到右下角的最短路线，入口点为[0,0],即第一格是可以走的路
输入描述：输入两个整数，分别表示二维数组的行数，列数。在输入相应的数组，其中的1表示墙壁，0表示可以走的路。数据保证有唯一解，不考虑多解的情况，即迷宫只有一条通道
输出描述：左上角到右下角的最短路径，格式如样列所示
输入：5 5
0 1 2 3 4 外围属于下标标识
0 0 1 0 0 0
1 0 1 1 1 0
2 0 0 0 0 0
3 0 1 1 1 0
4 0 0 0 1 0
输出
(0,0) (1,0) (2,0) (2,1) (2,2) (2,3) (2,4) (3,4) (4,4)

来到这个位置我相信很多的同学对题目的意思看的还不是很清楚，只是对输入和输出的描述有了一些的想法，但是这个位置我想建议同学们，我们一定在看到一个题目的时候不要先去看输入和输出的描述，一定要把题意给审清，否则我们很有可能就是因为没有把题目好好看，重点去关注输出和输入用例而导致我们做不出这个题目，当然那种大神级别的同学当然是有自己的做题方法的，那是因为人家已经是身经百战了，当时如果有刚开始做题目的同学，我们一定要把题意一个一个字的去研读清楚，然后再结合输入和输出用例来自我尝试解决这个问题，否则你就会发现很多题目不是做不了而是题意没有看清导致，所以这样就有一些适得其反了。所以接下来我们就来一起重新再研读一下这个题目。

1. 二维数组表示迷宫

2. 1表示步可以走，0表示可以走

3. 只能上下左右的走

4. 入口在左上角，出口在右下角

5. 只有唯一的一条通路（区别于下面的迷宫进阶问题）

6.（0，0）表示的就是入口

所以当我们弄清楚了这6点并且此时结合这输入和输出的用例，我们就可以开始思考如何实现这些要求了，切记，我们应该一个一个问题的想着如何可以更好的实现，不要把6个问题融合成一个问题来考虑如何实现，这个就是一个分割子问题的方法来解题，能减小我们的做题压力，并且发现自己的缺漏。

例如：第一步，我要实现用二维数组构造一个迷宫出来，所以我此时就应该先解决这个问题

想如何用二维数组构造迷宫呢？

假如此时你对二维数组这一块的知识掌握的还不是很好，或者是很久没有涉及过二维数组，有一些忘记了，此时我们就可以先去巩固或者复习一下二维数组的知识，然而搞明白了之后，我们再来解决眼前的这个问题。

当然这只是一个例子，我知道很多同学对二维数组玩的都是很好的，不像我。

但是我们碰到的所有问题都是这样，当我对这个小问题不理解的时候，我就应该要先去把整个小问题给解决，然后再来解决进一步的问题，一个一个小问题，最后解决大问题，然后一个一个大问题，最后成为算法大佬。

所以以上就是我个人对做题的一些浅薄见解

在此留作纪念，希望自己是一直这样做下去的，希望自己在以后的某一天，也有玩转算法的时候。并且此时希望看到这里的同学或者算法大佬能够分享一下自己的做题方法和指正我的做题方法。

所以这里我们正式开始对上面的问题进行解答

首先，我们想要找通路，就需要走起来，如何走起来呢？

此时就是判断我的maze[0][0]的上下左右是否有通路，有的话，我就走，这样我就可以从maze[0][0]的位置走到我的第二个位置了，但是此时当我来到第二个位置的时候，我还需要继续的走，我该从那个方向走呢？是上还是下，还是左，还是右呢？所以此时思路来到这里，我们就应该意识到有两个问题要解决了。

第一个问题：怎么走？

第二个问题：怎么一直走？

想明白这两个问题我们就可以很好的找到这条唯一的通路了

第一个问题

此时我们可以意识到想要走，我就要考虑应该往那个方向走，但是此时又要想到在迷宫中只有位置是0的位置才可以走，位置是1的并不可以走，并且我只能走上下左右不可以走斜线，想到了这几个点此时我们就应该要知道，我们应该要对maze[0][0]的上下左右进行判断，判断那个方向是0那个方向不是0，这样才可以在上下左右其中有0的时候，我就让它往数字0的位置走，并且当四个方向都没有0的时候，我们直接就可以返回这个迷宫没有通路。

bool IsPass(int** maze, int n, int m, position pos)
{
	if (pos.row >= 0 && pos.row < n && pos.col >= 0 && pos.col < m && maze[pos.row][pos.col] == 0)
	{
		return true;
    }
	else
	{
		return false;
	}
}

此时可以看出这个if语句中的条件就是判断我的下一个位置是可以走还是不可以走的

我们进行分步理解：

pos.row >= 0 && pos.row < n && pos.col >= 0 && pos.col < m

while (scanf("%d%d", &n, &m) != EOF)

此时的这两句代码中 row表示行 col表示列 n表示此时我们输入的n行，m表示我们输入的m列，此时就可以明显可以看出，我maze[0][0]想要走动起来，它的到达的下一个位置首先必须要满足这两个条件，也就是把maze[0][0]可以走的位置控制在我的二维数组之中，例：maze[0][0]此时肯定是不可以往上走的，所以就算此时maze[0][0]是0，它也不可以走，因为不在迷宫的范围之内。

并且此时代码中的 maze[pos.row][pos.col] == 0 就不用我说了吧！就是判断我的下一个位置是否为0，因为为0我才可以走，当然上面有提到，是在满足范围的前提之下。当然有的同学会不理解为什么是maze中的下标是[pos.row]和[pos.col]，那是因为此时我们可以把坐标给分装成一个结构体，利用结构体来表示我的坐标，如下所示：

typedef struct Position
{
	int row;
	int col;
}position;

但是思路来到这里，有的同学会问，不是要进行四个方向的判断吗？怎么没看见四个方向呢？这里是因为我们把四个方向的控制放在了如何一直进行四个方向的判断中了，也就是如何实现一直走的问题中了，当然这边我们先透露一下，主要就是涉及函数的递归。

第二个问题

此时我们解决了不管是maze[0][0]还是下一个位置的上下左右的判断，使我们可以找到前往下一个位置的通路了，但是此时当我再一次进行上下左右的判断是首先会有一个问题？只有解决这个问题我们才可以更好的进行第二个问题。

就是刚刚我的位置也就是上一个位置肯定是数字为0的位置，此时我再进行上下左右的判断的时候肯定是就会导致我走回头路的，所以我们要解决上一个位置为0的问题。

解决方法：就是每次当我要进行上下左右的判断通路的时候，先将上一个位置给置换成非0

此时我们就可以很好的进入到第二个问题了，也就是如何实现一直走的问题，也就是如何进行一直判断的问题，当然也就是这个迷宫题目中最核心的一步。当然这个问题的解决方法也可以帮我们解决当一个位置处有两个或两个以上的通路的时候，如何把每一条通路都给走一遍，然后找到那条真正可以到出口的通路和解决我如何从一条死路之中给返回到通路之中的问题。并且此时这个问题的解决方法就会涉及到了有关二叉树的深度优先遍历的问题，当我们在学习二叉树的时候，我们可以知道不管是我们遍历二叉树，还是算二叉树的叶子结点等问题都会涉及到递归二叉树的左子树和右子树的过程，所以此时我们就可以把迷宫中的四个方向的判断给想象成二叉树，相当于我的二叉树是判断两个方向而我的迷宫是判断四个方向，原理都是相同的，所以此时我们对四个方向的判断和找到死路后返回到通路和如何找到真正的通路都是使用我们二叉树中学的深度优先遍历来解决的，总之就是我们在二叉树中熟知的递归问题，在这个问题中我们也还是使用递归来解决，并且这里使用递归解决是非常合理有效的，一下就能解决弄的我们头痛的问题。

并且这边我们对二叉树的深度优先遍历做一个小小的回顾：

二叉树深度优先遍历：例： 0
0 0
0 0 0 0
0
0 最深的位置
表示的意思就是我先往深了走，就是一直往下走，直到走到最深的地方，此时走到最深的那个0的位置，此时不可以往下走了之后，我就返回，返回到上面的那个0，然后发现此时的这个0只有左子树没有右子树，所以再返回，同理没有右子树再返回，直到有右子树，此时就可以继续往我的右子树的方向走（也就是此时的右子树类似于我的迷宫的第二个通路，此时向第二个通路走），所以我的迷宫问题就非常像是我的二叉树的深度优先问题，所以此时通过这个深度优先的思想，我就可以解决多通路的问题了，并且这边如果不理解的话就可以想想自己当初画的或者是老师画的递归的展开图来结合着思考一下。

所以递归展开图是非常的重要的

我们结合代码来更好的分析一下：（代码中注释给全了，方便我们更好的理解代码）

bool GetMazePath(int** maze, int n, int m, position cur)
{
	StackPush(&path, cur);//此时就是将我的cur给入栈，但是要注意回溯的位置的坐标是不需要入栈的，所以要处理一下
	//但是此时我的递归是要有停止条件的（当然此时的停止条件也就是我找到了迷宫的出口就表示我递归的停止条件）
	if (cur.row == n - 1 && cur.col == m - 1)
	{
		return true;
	}
	//寻找通路
	//有了起始位置cur，此时我就开始探测我的cur位置的上下左右四个方向
	position next;
	maze[cur.row][cur.col] = 2;//就是直接把此时我在的这个位置给置成非0就行，这样就可以防止走回头路了

	//上
	next = cur;
	next.row -= 1;//表示next的上就是此时next的行的下标减1
	if (IsPass(maze, n, m, next))//此时这个就是判断此时的这个位置是否可以通
	{
		//GetMazePath(maze, n, m, next);//此时这个就是递归，把此时找到的通路next又重新给给我的cur，这样就可以完美的实现往下寻找通路
		//并且此时当我如果在上下左右中的其中之一已经找到了的话，我就可以不需要再找了，所以此时的这个函数需要判断一下，然后给一个返回值
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, n, m, next))//此时这个就是判断此时的这个位置是否可以通
	{
		//GetMazePath(maze, n, m, next);//此时这个就是递归，把此时找到的通路next又重新给给我的cur，这样就可以完美的实现往下寻找通路
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, n, m, next))//此时这个就是判断此时的这个位置是否可以通
	{
		//GetMazePath(maze, n, m, next);//此时这个就是递归，把此时找到的通路next又重新给给我的cur，这样就可以完美的实现往下寻找通路
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, n, m, next))//此时这个就是判断此时的这个位置是否可以通
	{
		//GetMazePath(maze, n, m, next);//此时这个就是递归，把此时找到的通路next又重新给给我的cur，这样就可以完美的实现往下寻找通路
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}

	StackPopt(&path);//这个位置来一个出栈，就可以很好的解决我的回溯问题，因为return false 就是说明这个坐标的位置处不是我的通路，所以在return false之前出栈，就是我最好的时机 
	return false;//表示只要上述有任何一个位置可以通就会return true; 上述四个位置都不可以通此时代码就来到这个位置就return false;
}

我们此时先不管入栈和出栈的问题，待会再细细的把入栈出栈的问题分析清楚，我们先分析有关迷宫的走法上的，先不管迷宫通路的打印问题。

例：此时的这句代码就是我的出口所在的位置，因为由题意可以知道出口是在右下角的，所以只需要把row和col的坐标控制在（n-1，m-1）处就可以找到出口了，并且可以明显看出此时的这个if语句中的条件和这个if语句就是我的递归条件，递归停止的条件。

	if (cur.row == n - 1 && cur.col == m - 1)
	{
		return true;
	}

例：此时的next就是我们上述所说的结构体中的row和col的位置，也就是坐标位置，并且maze[cur.row][cur.col] = 2; 这句代码就是为了在我走到了通路，来到了下一个位置，要进行下一次的上下左右进行判断的时候，先把我的上一个位置给置换成非0，然后这样才可以防止走回头路

	position next;
	maze[cur.row][cur.col] = 2;//就是直接把此时我在的这个位置给置成非0就行，这样就可以防止走回头路了

例： next = cur;这句代码表示的就是把cur的坐标给给我的next，例如当我现在是在maze[0][0]的位置，也就是把入口的位置先从下面的主函数（main）中传值上来，然后对其进行相应坐标的加减，这样我就可以很好的表示出maze[0][0]的上下左右的位置了，所以此时的的maze[-1][0] 、maze[1][0] 、maze[0][-1] 、maze[0][1] ，就是表示maze[0][0] 的上下左右的位置的坐标，如下代码中：

    //上
    next = cur;
    next.row -= 1;

    //下
    next = cur;
    next.row += 1;

    //左
    next = cur;
    next.col -= 1;

    //右
    next = cur;
    next.col += 1;

来到这个位置之后，我们就已经将本题中的代码：

bool GetMazePath(int** maze, int n, int m, position cur)

中除了有关栈的使用以外的内容给讲完了，此时我们就要开始最让人头痛的递归回溯的过程的代码讲解了。


bool GetMazePath(int** maze, int n, int m, position cur)
{
    //上
    next = cur;
    next.row -= 1;
	if (IsPass(maze, n, m, next))
	{
		GetMazePath(maze, n, m, next);

	}
    //下
    next = cur;
    next.row += 1;
	if (IsPass(maze, n, m, next))
	{
		GetMazePath(maze, n, m, next);

	}
    //左
    next = cur;
    next.col -= 1;
	if (IsPass(maze, n, m, next))
	{
		GetMazePath(maze, n, m, next);

	}
    //右
    next = cur;
    next.col += 1;
	if (IsPass(maze, n, m, next))
	{
		GetMazePath(maze, n, m, next);

	}
}

此时可以看出我的上述代码就是一个通过上一个位置来找此时这个位置上下左右的位置的代码和判断上下左右是否是通路（0和非0）的代码，并且我们不难看出我们是把这句用来实现一直走的代码GetMazePath(maze, n, m, next); 放在了我的if语句之中，所以我们的目的就是为了让上下左右的位置先要满足是通路的条件之后，我们才开始重新调用 GetMazePath(maze, n, m, next); 也就是实现一直调用一直走，所以只要是通路（0）我们就可以继续往下走，当不是通路（非0）的情况下，我们就不调用，然后程序继续执行，然后就可以依次对上下左右都给进行判断了。

但是此时代码按照上面这样写，我们的程序就出大问题了，就是假如我在一处通路位置处，此时的这个位置的通路又不止有一条通路而是有多条通路，但是这些通路中又只有一条是可以最终到达我的终点的位置，但是如果我不进行处理的话，假如按照上述代码的原理，我走进的是一条死路，最终就会导致我的死路的最后一个位置的上下左右都是非0，就会导致本来我这个迷宫是有通路的，只是你走错了，导致最后返回的是没找到出口这个结果，所以我们的代码是有问题的。

解决方法：就是每当我找到一条通路之后，我就不找了，然后此时通过神奇的回溯递归原理来实现当我找到的是死路的回溯和各个通路的判断唯一终点的问题

代码如下：

bool GetMazePath(int** maze, int n, int m, position cur)
{
    //上
    next = cur;
    next.row -= 1;
	if (IsPass(maze, n, m, next))
	{
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}
    //下
    next = cur;
    next.row += 1;
	if (IsPass(maze, n, m, next))
	{
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}
    //左
    next = cur;
    next.col -= 1;
	if (IsPass(maze, n, m, next))
	{
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}
    //右
    next = cur;
    next.col += 1;
	if (IsPass(maze, n, m, next))
	{
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}
}

此时这样写，我们就真的是把递归的精华给用出来了（如果不明白就参考坐标图来进行递归展开图的描画）反正目的就是上述所说，回溯和找唯一出口。

———————————————————————————————————————————

解决了上述的两个问题，我们算是把如何迷宫问题的最大的问题，如何顺利的走出迷宫的问题给解决了。假如看到了这，赶紧奖励自己一朵小红花！刻不容缓！快马加鞭！

———————————————————————————————————————————

搞定了本质问题之后，我们着手一些其它的问题

例：我相信这里很多的同学使用的都是VS这个编译器，不管你用的是几几年的VS，我在这里告诉你，VS是都不允许定义变长数组的，那么此时就有同学会问，我应该如何定义一个不限定大小的二维数组呢？如果不会的话，这边有详细教学哦！不过我相信你们都是会的。并且此时就是涉及到一个与指针数组相关的知识。

动态开辟二维数组原理：就是开辟先开辟一个一维数组出来，但是此时这个一维数组中的数据类型不是int 也不是 char 而是 int* ，没错就是一个指针类型的数组，就像是装了一卡车炸弹的卡车的感觉有没有（反正这边我某明就联想到了），然后用这个数组中的指针再去指向我的一维数组。

所以不难想到我的第一个一维数组中有几个指针，就可以指向几个一维数组，也就表示有n个指针，我就有n个一维数组，然后我就有了一个二维数组了（因为二维数组本身就是由一位数组构成的）

文字图示：

一 -> 一维数组
维 -> 一维数组 =>这样我就开辟出来了一个二维数组了
数 -> 一维数组
组 -> 一维数组

动态开辟二维数组代码：

int main()
{
    int** maze = (int**)malloc(sizeof(int*) * n);
	for (int i = 0; i < n; i++)
	{
		maze[i] = (int*)malloc(sizeof(int) * m);
	}
}

*n表示的就是乘n，*m表示的就是乘m，因为我要用n行那就是有n个一维数组，每个数组m大小，就是表示m列。

———————————————————————————————————————————

思路来到这里我们就直接要开始讲我们的第二重要的问题了，应该返回通路的坐标呢？

这里我们就涉及到了与数据结构中栈有关的知识了

有的同学会问，为什么跟栈有关系呢？

这边我们做一个讲解：首先想象一下，我从maze[0][0] 的位置开始走，最后走到了出口，我是不是是正着走的啊，我们一步一步打印不就行了吗？但是你再想，其实还是那个老问题，讲了好几遍了，就是当我此时的某一个位置有不止一个通路的时候，我的正确的通路却只有一条，按照我的代码原理，我是要一条通路一条通路的去走，最终才可以找到有出口的那条通路，所以此时你就可以知道，我是会走到死路中去的，但是死路不是我要的，所以不可以打印，所以我要把这条死路的每一个坐标删除之后，我是不是才可以打印啊！但是我要如何去删除死路的每一个坐标呢？可以发现我一定要从后往前删，才可以在回溯的过程中将我的每一个死路坐标给全部删除。刚好后进先出，这就是数据结构中栈的神奇特性。所以这就是涉及到栈的原因。

但是此时如果我们用C语言去实现的话就会非常的麻烦，麻烦在C语言中是没有栈这个库函数的，需要我们自己去实现一个栈，所以此时不用我多说了，就是去实现一个栈出来供我们存放数据和删除数据。

数据结构中栈的实现代码：（如果有不懂的东西可以先去复习一下什么是栈和栈的具体实现）

typedef position STDataType;//此时我的栈中存放的不是一个整形，存放的是一个坐标，所以存放的类型是position
typedef struct Stack
{
	STDataType* data;
	int top;
	int capacity;
}Stack ,ST;

//弄完了结构体我们现在就要弄几个主要的接口函数

//函数的声明
void StackInit(ST* ps);
void StackDestory(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPopt(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool StackEmpty(ST* ps);

//函数的实现
void StackInit(ST* ps)
{
	assert(ps);
	ps->data = NULL;
	ps->top = 0;
	ps->capacity = 0;
}
//销毁
void StackDestory(ST* ps)
{
	free(ps->data);
	ps->data = NULL;
	ps->capacity = 0;
	ps->top = 0;

}
//栈顶插入
void StackPush(ST* ps, STDataType x)
{
	assert(ps);

	if (ps->capacity == ps->top)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->data = tmp;
		ps->capacity = newCapacity;
	}

	ps->data[ps->top] = x;
	ps->top++;
}
//栈顶删除
void StackPopt(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}
//寻找栈顶
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->data[ps->top - 1];
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{

	return ps->top == 0;
}
int StackSize(ST* ps)
{

	return ps->top;

}

typedef position STDataType;然后因为此时我的栈中存放的不是一个整形，存放的是一个坐标，所以存放的类型要改成position，这样才可以符合我的使用。

有了这个栈，我们就可以很好的解决上述的那个删除死路数据的问题了，在GetMazePath()函数的头位置放上一个栈的输入，在尾位置放上一个栈的删除，因为代码太长的原因，我就不演示了，直接讲解就行，例如：此时根据回溯原理和递归展开图等多方面的想象，我可以知道，什么时候会开始我的回溯，显然是在我四个方向的位置都是非0的情况下，我就会开始回溯，但是如果我此时在GetMazePath() 函数的尾位置放了一个栈的删除，当我进行判断，发现四个位置都走不通的时候，此时就会随着程序的向下走，来到我的栈的删除的代码，此时执行一个栈的删除，刚好就可以把我最后录入的那个死路的最后一个位置的坐标给删除掉。同理删除别的位置的坐标，直到有找到通路开始递归。

———————————————————————————————————————————

搞到这里我们就已经把所有的问题给解决了，掌声鼓励！啪！啪！啪！啪！啪！啪！

剩下了最后一步已经不是问题了，就是一个普通的栈中元素的输出而已，只要把这个栈给输出，我们就获得了唯一的一条通路的坐标了，我们就搞定这个题目了。

代码如下：

void PrintPath(ST* path)//函数目的：输出栈里面的坐标
{
	//但是此时要怎么使用栈输出呢？
	//原理：使用两个栈，把我这个栈中的数据导入到另一个栈中，这样我就有了正的数据了，然后再出这个栈，就是就完成题意了
	//所以下述的代码就是为了：将我的path中的数据导入到rangePath中
	Stack rangePath;
	StackInit(&rangePath);
	while (!StackEmpty(path))
	{
		StackPush(&rangePath, StackTop(path));
		StackPopt(path);
	}

	while (!StackEmpty(&rangePath))
	{
		position top = StackTop(&rangePath);
		printf("(%d,%d)\n", top.row, top.col);
		StackPopt(&rangePath);
	}

	//销毁栈，好习惯
	StackDestory(&rangePath);
}

但是一提交我们发现，我们错了，为什么呢？说明我们的掌声是拍早了。

因为我们是把数据存到栈中，所以我们发现，想要从栈中拿数据拿的是后到前的，但是题意是前到后，所以我们就需要想上述代码一样，再建一个新的栈，把开头存放数据的栈中的数据导入到新的栈中，这样我们就实现了栈中的数据的顺序的调换，此时我们再把新栈中的数据输出，就发现大功告成了，是的，我们大功告成了。

但是这边我给到两个注意点：就是要注意栈的初始化和栈的销毁的同时记得将我们动态内存开辟出来的数组空间给释放掉

到这我们就可以宣布大功告成了！欧耶！耶耶耶耶耶！

———————————————————————————————————————————

当然身为一个贴心的博主，我肯定是会把完整的并且通过了全部测试用例的代码放在这里的，请放心啦！

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<string.h>

typedef struct Position
{
	int row;
	int col;
}position;


//因为我要有一个栈来存放我的每一个通路的坐标位置，所以我要有一个栈
//栈的代码：
typedef position STDataType;//此时我的栈中存放的不是一个整形，存放的是一个坐标，所以存放的类型是position
typedef struct Stack
{
	STDataType* data;
	int top;
	int capacity;
}Stack ,ST;

//弄完了结构体我们现在就要弄几个主要的接口函数

//函数的声明
void StackInit(ST* ps);
void StackDestory(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPopt(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool StackEmpty(ST* ps);

//函数的实现
void StackInit(ST* ps)
{
	assert(ps);
	ps->data = NULL;
	ps->top = 0;
	ps->capacity = 0;
}
//销毁
void StackDestory(ST* ps)
{
	free(ps->data);
	ps->data = NULL;
	ps->capacity = 0;
	ps->top = 0;

}
//栈顶插入
void StackPush(ST* ps, STDataType x)
{
	assert(ps);

	if (ps->capacity == ps->top)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->data = tmp;
		ps->capacity = newCapacity;
	}

	ps->data[ps->top] = x;
	ps->top++;
}
//栈顶删除
void StackPopt(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}
//寻找栈顶
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->data[ps->top - 1];
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{

	return ps->top == 0;
}
int StackSize(ST* ps)
{

	return ps->top;

}
/

//迷宫代码：
Stack path;

void PrintMaze(int** maze, int n, int m)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			printf("%d ", maze[i][j]);
		}
		printf("\n");

	}
}

void PrintPath(ST* path)//函数目的：输出栈里面的坐标
{
	//但是此时要怎么使用栈输出呢？
	//原理：使用两个栈，把我这个栈中的数据导入到另一个栈中，这样我就有了正的数据了，然后再出这个栈，就是就完成题意了
	//所以下述的代码就是为了：将我的path中的数据导入到rangePath中
	Stack rangePath;
	StackInit(&rangePath);
	while (!StackEmpty(path))
	{
		StackPush(&rangePath, StackTop(path));
		StackPopt(path);
	}

	while (!StackEmpty(&rangePath))
	{
		position top = StackTop(&rangePath);
		printf("(%d,%d)\n", top.row, top.col);
		StackPopt(&rangePath);
	}

	//销毁栈，好习惯
	StackDestory(&rangePath);
}

bool IsPass(int** maze, int n, int m, position pos)
{
	if (pos.row >= 0 && pos.row < n && pos.col >= 0 && pos.col < m && maze[pos.row][pos.col] == 0)//就是限制范围和判断此时上下左右的数据是否是0,是0就可以通，否则就不行
	{
		return true;
    }
	else
	{
		return false;
	}
}

bool GetMazePath(int** maze, int n, int m, position cur)
{
	StackPush(&path, cur);//此时就是将我的cur给入栈，但是要注意回溯的位置的坐标是不需要入栈的，所以要处理一下
	//但是此时我的递归是要有停止条件的（当然此时的停止条件也就是我找到了迷宫的出口就表示我递归的停止条件）
	if (cur.row == n - 1 && cur.col == m - 1)
	{
		return true;
	}
	//寻找通路
	//有了起始位置cur，此时我就开始探测我的cur位置的上下左右四个方向
	position next;
	maze[cur.row][cur.col] = 2;//就是直接把此时我在的这个位置给置成非0就行，这样就可以防止走回头路了

	//上
	next = cur;
	next.row -= 1;//表示next的上就是此时next的行的下标减1
	if (IsPass(maze, n, m, next))//此时这个就是判断此时的这个位置是否可以通
	{
		//GetMazePath(maze, n, m, next);//此时这个就是递归，把此时找到的通路next又重新给给我的cur，这样就可以完美的实现往下寻找通路
		//并且此时当我如果在上下左右中的其中之一已经找到了的话，我就可以不需要再找了，所以此时的这个函数需要判断一下，然后给一个返回值
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, n, m, next))//此时这个就是判断此时的这个位置是否可以通
	{
		//GetMazePath(maze, n, m, next);//此时这个就是递归，把此时找到的通路next又重新给给我的cur，这样就可以完美的实现往下寻找通路
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, n, m, next))//此时这个就是判断此时的这个位置是否可以通
	{
		//GetMazePath(maze, n, m, next);//此时这个就是递归，把此时找到的通路next又重新给给我的cur，这样就可以完美的实现往下寻找通路
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, n, m, next))//此时这个就是判断此时的这个位置是否可以通
	{
		//GetMazePath(maze, n, m, next);//此时这个就是递归，把此时找到的通路next又重新给给我的cur，这样就可以完美的实现往下寻找通路
		if (GetMazePath(maze, n, m, next))
		{
			return true;
		}
	}

	StackPopt(&path);//这个位置来一个出栈，就可以很好的解决我的回溯问题，因为return false 就是说明这个坐标的位置处不是我的通路，所以在return false之前出栈，就是我最好的时机 
	return false;//表示只要上述有任何一个位置可以通就会return true; 上述四个位置都不可以通此时代码就来到这个位置就return false;
}
int main()
{
	//有了上述的思路，开始吧！
	//1.输入两个数，弄一个数组出来
	int n = 0;
	int m = 0;
	while (scanf("%d%d", &n, &m) != EOF)//此时因为我可能有多组迷宫，所以我们这边要使用循环输入
	//scanf("%d%d", &n, &m);
	{
		//
// 动态开辟二维数组思路
// 
//int arr[n][m]; =>这个叫变长数组，但是vs不支持，有的新版编译器是支持的
//int arr[][] = { 0 };
//因为我的vs不支持变长数组，所以我们需要去动态开辟一个二维数组（此时就会涉及到指针数组的相关知识）
//为什么会涉及到指针数组的相关知识呢？
//原因就是，开辟数组时，不可以直接开辟二维数组，只能开辟一维数组，但是此时可以通过这个一维数组去指向别的一维数组（这样就可以类似的是开辟了一个二维数组了）
//图示：
//  一 -> 一维数组
//  维 -> 一维数组   =>这样我就开辟出来了一个二维数组了
//  数 -> 一维数组
//  组 -> 一维数组
// 
// 动态开辟二维数组代码
// 
//有了这个思路，开辟一个一维数组代码如下：
//int* arr = (int*)malloc(sizeof(int) * n);//此时就是说明我这个数组中有n个int类型的元素 （整形）
//有了开辟普通一维数组的思路，我们就可以模仿者开辟一个有n个指针的一维数组出来，所以开辟一个二维数组代码如下：
		int** maze = (int**)malloc(sizeof(int*) * n);//此时就是说明我这个数组中有n个int*类型的元素 （指针） =>  就是为了可以很好的指向我的其它的n个一维数组
		for (int i = 0; i < n; i++)
		{
			maze[i] = (int*)malloc(sizeof(int) * m);//此时就是让这个maze数组中的n个指针去指向我的m个开辟出来的二维数组
		}

		//开辟完二维数组就是拿来用的，所以现在要开始我的二维数组的输入了
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < m; j++)
			{
				scanf("%d", &maze[i][j]);//输入记得要取地址
			}

		}
	//	PrintMaze(maze, n, m);
		//2.寻找通路
		StackInit(&path);//此时一定要记得把我的栈给初始化一下，然后再去使用它

		position entry = { 0,0 };//将我的出发位置传上去，因为出发位置是一个二维的坐标（所以可以直接创建一个结构体来表示）
		if (GetMazePath(maze, n, m, entry))
		{

			PrintPath(&path);
		}
		else
		{
			printf("没有找到通路,要命\n");
		}

		//栈用完之后就是销毁，好习惯
		StackDestory(&path);


		//此时代码来到这个位置我们就要想到释放动态内存
		for (int i = 0; i < n; i++)
		{
			free(maze[i]);
		}
		free(maze);
		maze = NULL;
	
	}

	return 0;
}

————————————————————————————

2.迷宫进阶问题

题目我们直接贴图

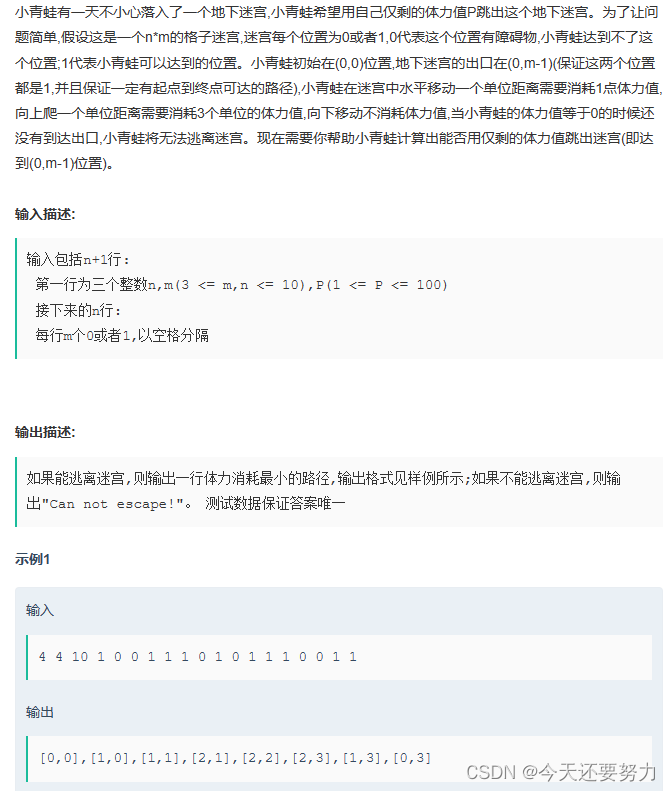
还是上述的对于读题的理解，读题是很关键的，所以我们此时再研读一遍题目，然后明白题目中的几个主要问题

1. 用体力值P跳出这个地下迷宫
2. 一个n*m的迷宫
3. 0代表障碍物，1代表通路
4. 初始在(0,0)位置,出口在(0,m-1)

5. 一定有起点到终点可达的路径
6. 水平移动一个位置消耗1点体力值
7. 向上一个位置消耗3点体力值
8. 向下移动不消耗体力值

9. 体力值为0还没有出去表示出不去

本质其实还是一个初阶迷宫的问题，只不过是需要玩的东西变多了一点而已

例如：我们先思考一下体力值的问题，其实这个体力值的问题不就是在我判断上下左右的时候，同时也就可以实现吗？不是就当我把maze[0][0] 的上下左右的位置找出来之后，然后就可以对体力值进行加减了吗？所以明白了这个，我们就可以这样写。

首先在输入数值的时候多输入一个p给它，就代表着我的体力值。

例：while (scanf("%d%d", &n, &m, &p) != EOF)；

有了体力值之后，就把这个体力值当做一个参数传给别的函数使用，具体代码如下：

void GetMazePath(int** maze, int n, int m, position cur, int p)//第一个改进不要返回值
{
	StackPush(&path, cur);

	position next;
	maze[cur.row][cur.col] = 2;

	//上
	next = cur;
	next.row -= 1;
	if (IsPass(maze, n, m, next))
	{
		(GetMazePath(maze, n, m, next, p - 3));//就是根据题意向上就是消耗3个体力值

	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, n, m, next))
	{
		(GetMazePath(maze, n, m, next, p));//向下就是不消耗
	
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, n, m, next))
	{
		(GetMazePath(maze, n, m, next, p - 1));//水平移动就是消耗一个

	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, n, m, next))
	{
		(GetMazePath(maze, n, m, next, p - 1));//水平移动就是消耗一个

	}
	maze[cur.row][cur.col] = 1;
	StackPopt(&path);
}

这样就很好的解决了我的体力值和我的上下左右的问题了

下面我们只需要把和通路和墙壁给改动一下和终点的位置给改动一下，我们的代码在迷宫这个层面上就没有什么大问题了，剩下的和迷宫问题关系都不是很大，涉及的更多的都是数据结构了。

改动通路和墙壁：

bool IsPass(int** maze, int n, int m, position pos)
{
	if (pos.row >= 0 && pos.row < n && pos.col >= 0 && pos.col < m && maze[pos.row][pos.col] == 1)
	{
		return true;
	}
	else
	{
		return false;
	}
}

可以看出此时我的通路从0变成了1

改动终点：

void GetMazePath(int** maze, int n, int m, position cur, int p)
{
	StackPush(&path, cur);
	if (cur.row == 0 && cur.col == m - 1)
}

可以看出我将我的终点从右下角改成了右上角

此时我们进行了这几个地方的改进，会发现我们可以通过20%的测试用例了，这说明，我们的代码是朝着正确的方向进行的。

所以我们再把几个地方给处理一下，我们就搞定这个题目了

———————————————————————————————————————————

重大问题的改动

1. 第一个问题：
我们在做第一题的时候，我们是固定只需要有一条通路通过了就行了,但是此时的这个题目是要求我们把所有的通路都找出来，然后进行比较,比较出花费的体力最少的那一个才是我要的通路。

所以方法就是把所有的通路找出来，然后进行通路的花费体力的比较，就可以很好的解决本问题了

但是我们应该如何找出所有的通路并且找出最短的那条通路呢？我们此时就可以再一次的很好的利用栈的特性，我再重新创建一个新的栈，让之前的栈去找迷宫中的通路，然后把找到的通路复制到我的新的栈中，然后再让之前的那个栈去找通路，然后两条通路进行比较，把短的那条再一次的复制给我的新的栈，重复类推，直到找到最短的通路为止。代码如下：

void GetMazePath(int** maze, int n, int m, position cur, int p)//第一个改进不要返回值
{
	StackPush(&path, cur);
	if (cur.row == 0 && cur.col == m - 1)
	{
		if (p >= 0 && StackEmpty(&minPath) || StackSize(&path) < StackSize(&minPath))
		{
			//minPath = path  //这边切记不可以使用直接赋值的方式
			StackDestory(&minPath);
			//然后这里就会涉及到一个深拷贝问题了
			StackCopy(&path, &minPath);//类似strcopy


		}
	}
}

但是此时这个问题中的复制问题切记不可以直接使用赋值的方法（因为会涉及到一个深拷贝的问题）具体在下面讲到这个函数的时候进行讲解。

2. 第二个问题：
就是当我有两条通路有公共的通路的时候，此时第一条通路走完之后会把这条通路都给置成2，此时就会导致原来本来另一条通路也可以走，但是变成2之后，就不能走了，所以我们再走的过程中把1变成了2之后，要重新给它变回来，不然就会出问题，所以按照原理，就要把刚刚1改成2的地方给重新恢复成1。
所以我们要在这个void GetMazePath(int** maze, int n, int m, position cur, int p)，函数的尾位置放上一个maze[cur.row][cur.col] = 1; 的代码，就是表示把2恢复成1，只有恢复成1，我的下一条通路才可以也走成功，否则我就找不到所有的通路。
然后恢复完公共路径之后，我们来到第三个问题。

3.第三个问题：
涉及更新的问题
就是我的递归此时会把我的所有的通路都给走一遍，而在走一遍的过程中，每一次都会把这些通路的坐标给如到栈中去，所以如果不将栈进行一定的更新，此时我的栈中就会放着很多的东西
所以我们需要把栈进行更新，才可以实现，每一次栈中放的东西都是一条特定的通路而不是重复的通路
按照上述的代码，我是把路径记录在我的path中，所以我就是要对我的path进行更新就可以了
所以此时我就要给一个新的栈 Stack minPath; 来辅助我的 Stack path; 来进行我的栈的更新
if (StackEmpty(&minPath) || StackSize(&path) < StackSize(&minPath)) 此时就是表示我的minPath中还没有元素或者此时的path栈中的元素个数比minPath栈中的元素个数小（也就是通路的长短的判断），此时这两个条件成立一个都可以进到我的if语句之中
minPath = path; 但是这边切记不可以使用直接赋值的方式。因为如果直接赋值的话，就会涉及下面这两个问题了。

1.这样直接赋值会有内存泄露的风险,因为我是直接把我的path给给我的minPath，此时的原理的minPath的内存就会丢失
2.就是当我的path重新去找通路的时候，此时path会找到死路，找到死路本身是没有问题的，因为死路之后会回溯回来，回溯回来的过程中，会有删除的过程，在这个删除的过程之中就会出大问题
为什么呢？因为我把我的minPath直接赋值给path此时会使minPath和path指向的是同一块空间，然后在删除path的过程中，就会把我的minpath也给删除，所以就会有问题

解决方法：1.我要把minPath这个栈先给销毁掉 2.然后再进行拷贝：但是会涉及到一个深拷贝问题了

深拷贝：在销毁minPath的空间之后，重新开辟一个和path一样大的空间，然后再把path中的元素拷贝到minPath此时的这个独立空间之中就行了
如何拷贝呢？此时我们就再实现一个类似strcopy的StackCopy函数，然后再进行传址交换StackCopy(&path, &minPath); 代码如下：

void StackCopy(Stack* ppath, Stack* pminPath)
{
	pminPath->data = (STDataType*)malloc(sizeof(STDataType*) * ppath->capacity);
	memcpy(pminPath->data, ppath->data, sizeof(STDataType) * ppath->top);//直接将ppath中数据的值拷贝给pminPath（因为此时的空间的大小是一样的，所以不会出问题的）
	pminPath->top = ppath->top;
	pminPath->capacity = ppath->capacity;//此时这个位置就是叫做浅拷贝的问题
}

这个函数的意思就是先开辟一个和原栈相同大小的空间之后，再我接收原栈中的元素，然后还有top和capacity；

4. 第四个问题
此时代码来到这里，剩下的问题就是体力值的问题了
所以我们要把体力值的问题解决一下，解决方法就是当我的p不大于0的时候我就不会进行栈的更新，这样就可以很好的把体力值不够的那条通路给排除掉了
if (p >= 0 && StackEmpty(&minPath) || StackSize(&path) < StackSize(&minPath))
所以此时我们这种写法，体力值就只是用来判断我找的通路是有效的还是无效的而已，并没有直接和我的通路的长短挂钩

_____________________________________________________________________________

所以以上就是迷宫的进阶的题目，解释的效果可能没有初阶好，因为现在有点迟了，今天看了一下电视，然后导致写博客的时间有点紧了，所以请见谅！

当然细心的我，还是会把完整代码发出来的啦！

typedef struct Position
{
	int row;
	int col;
}position;


//因为我要有一个栈来存放我的每一个通路的坐标位置，所以我要有一个栈
//栈的代码：
typedef position STDataType;//此时我的栈中存放的不是一个整形，存放的是一个坐标，所以存放的类型是position
typedef struct Stack
{
	STDataType* data;
	int top;
	int capacity;
}Stack, ST;

//弄完了结构体我们现在就要弄几个主要的接口函数

//函数的声明
void StackInit(ST* ps);
void StackDestory(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPopt(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool StackEmpty(ST* ps);

//函数的实现
void StackInit(ST* ps)
{
	assert(ps);
	ps->data = NULL;
	ps->top = 0;
	ps->capacity = 0;
}
//销毁
void StackDestory(ST* ps)
{
	free(ps->data);
	ps->data = NULL;
	ps->capacity = 0;
	ps->top = 0;

}
//栈顶插入
void StackPush(ST* ps, STDataType x)
{
	assert(ps);

	if (ps->capacity == ps->top)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->data = tmp;
		ps->capacity = newCapacity;
	}

	ps->data[ps->top] = x;
	ps->top++;
}
//栈顶删除
void StackPopt(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}
//寻找栈顶
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->data[ps->top - 1];
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{

	return ps->top == 0;
}
int StackSize(ST* ps)
{

	return ps->top;

}
/

//迷宫代码：
Stack path;
//因为我每次都要更新我的栈，所以此时我就还要再给一个栈
Stack minPath;

void PrintMaze(int** maze, int n, int m)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			printf("%d ", maze[i][j]);
		}
		printf("\n");

	}
}

void PrintPath(ST* path)
{
	Stack rangePath;
	StackInit(&rangePath);
	while (!StackEmpty(path))
	{
		StackPush(&rangePath, StackTop(path));
		StackPopt(path);
	}

	while (StackSize(&rangePath) > 1)//此时这样写的目的就是为了控制最后一个不打印逗号而已，其它前面的Size-1个都需要打印逗号
	{
		position top = StackTop(&rangePath);
		printf("[%d,%d],", top.row, top.col);
		StackPopt(&rangePath);
	}

	position top = StackTop(&rangePath);
	printf("[%d,%d],", top.row, top.col);
	StackPopt(&rangePath);


	//销毁栈，好习惯
	StackDestory(&rangePath);
}

bool IsPass(int** maze, int n, int m, position pos)
{
	if (pos.row >= 0 && pos.row < n && pos.col >= 0 && pos.col < m && maze[pos.row][pos.col] == 1)//就是限制范围和判断此时上下左右的数据是否是0,是0就可以通，否则就不行
	{
		return true;
	}
	else
	{
		return false;
	}
}

void StackCopy(Stack* ppath, Stack* pminPath)
{
	//StackInit(pminPath);//注意此时已经是指针了，不敢哪里都传地址
	//for (int i = 0; i < ppath->top; i++)//因为此时的ppath是一个指针所以可以使用->,而下面的cur只是一个结构体，所以不可以使用->,只能用 . =>来解引用
	//{
	//	StackPush(pminPath, ppath->data[i]);
	//}
	//此时除了上述的这种方法，还有就是下面这种更简单一些的方法
	pminPath->data = (STDataType*)malloc(sizeof(STDataType*) * ppath->capacity);
	memcpy(pminPath->data, ppath->data, sizeof(STDataType) * ppath->top);//直接将ppath中数据的值拷贝给pminPath（因为此时的空间的大小是一样的，所以不会出问题的）
	pminPath->top = ppath->top;
	pminPath->capacity = ppath->capacity;//此时这个位置就是叫做浅拷贝的问题
}

//bool GetMazePath(int** maze, int n, int m, position cur, int p)
void GetMazePath(int** maze, int n, int m, position cur, int p)//第一个改进不要返回值
{
	StackPush(&path, cur);
	if (cur.row == 0 && cur.col == m - 1)
	{
		//首先如果程序可以来到这里就是表示我已经找到了一条通路了
		//然后对通路进行判断
		//如果此时找到的通路比上一条通路更短，此时我就进行minPath的更新
		if (p >= 0 && StackEmpty(&minPath) || StackSize(&path) < StackSize(&minPath))//此时就是表示我的minPath中还没有元素或者此时的path栈中的元素个数比minPath栈中的元素个数小（也就是通路的长短的判断），此时这两个条件成立一个都可以进到我的if语句之中
		{
			//minPath = path  //这边切记不可以使用直接赋值的方式
			StackDestory(&minPath);
			//然后这里就会涉及到一个深拷贝问题了
			StackCopy(&path, &minPath);//类似strcopy


		}
	}
	position next;
	maze[cur.row][cur.col] = 2;

	//上
	next = cur;
	next.row -= 1;
	if (IsPass(maze, n, m, next))
	{
		(GetMazePath(maze, n, m, next, p - 3));//就是根据题意向上就是消耗3个体力值

	}

	//下
	next = cur;
	next.row += 1;
	if (IsPass(maze, n, m, next))
	{
		(GetMazePath(maze, n, m, next, p));//向下就是不消耗
	
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPass(maze, n, m, next))
	{
		(GetMazePath(maze, n, m, next, p - 1));//水平移动就是消耗一个

	}

	//右
	next = cur;
	next.col += 1;
	if (IsPass(maze, n, m, next))
	{
		(GetMazePath(maze, n, m, next, p - 1));//水平移动就是消耗一个

	}
	//此时代码来到这里就是表示我找到了某一条通路，此时我按照原理，就要把刚刚1改成2的地方给重新恢复成2
	maze[cur.row][cur.col] = 1;//只有恢复成1，我的下一条通路才可以也走成功，否则我就找不到所有的通路
	StackPopt(&path);
}
int main()
{
	int n = 0;
	int m = 0;
	int p = 0;
	while (scanf("%d%d", &n, &m, &p) != EOF)
	{
		int** maze = (int**)malloc(sizeof(int*) * n);
		for (int i = 0; i < n; i++)
		{
			maze[i] = (int*)malloc(sizeof(int) * m);
		}

		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < m; j++)
			{
				scanf("%d", &maze[i][j]);//输入记得要取地址
			}

		}
		PrintMaze(maze, n, m);
		//2.寻找通路
		StackInit(&path);
		StackInit(&minPath);//用了栈就一定要记得初始化

		position entry = { 0,0 };
		GetMazePath(maze, n, m, entry, p);

		if (!StackEmpty(&minPath))//此时就是表示我的栈有更新（有更新也就是说明我有找到更短的通路）
		{
			PrintPath(&minPath);
		}
		else//else就是表明我没有进行栈的更新，没有进行栈的更新也就是说明没有更短的通路，也就是说明我体力值不够，出不去
		{
			printf("Can not escape!\n");
		}
		

		StackDestory(&path);
		StackDestory(&minPath);//用了栈就要记得销毁
		for (int i = 0; i < n; i++)
		{
			free(maze[i]);
		}
		free(maze);
		maze = NULL;

	}

	return 0;
}