---

一、什么是熵？

 
熵，entropy，一个简简单单的字却撑起了机器学习的半壁江山，熵起源于热力学，代表一个热力系统的混乱程度，系统越混乱，熵越大。而机器学习中的熵是信息熵，是香农借鉴热力学熵而创造的概念。
 
本节的说明是借鉴王木头的YouTube视频而来的。
 
讨论熵的概念之前，先要解释清楚的是信息量这个概念，信息量的定性说明：针对某个不确定事件，将其变为确定性事件所需要的信息含量的度量。我们先不从定量的角度定义信息量，而是先给一个例子来说明不同情况下的不同信息量大小：
 
少年时期的迈特凯和卡卡西，参加忍者学校入学考试，毫无疑问，身为天才的卡卡西几乎是一定可以顺利通过入学考试，换而言之，顺利入学概率很大，接近100%，假设为99%；相反，常年被嘲笑的吊车尾迈特凯顺利入学的概率就小的多了，我们假设为10%。现在入学考试已经举行完毕，入学名单也公布了，但是你还没有看，我告诉你说卡卡西顺利入学，你很可能会说，这也没什么信息量，卡卡西那么强，入学不是理所当然的事情吗，但是我又告诉你，迈特凯也通过了入学考试，你很可能会感到惊讶，这个结果信息量太大了，这个吊车尾竟然也可以通过考试。
 
以上的例子就说明，一个事件发生概率越低，这件事由不确定变成确定事件所需要的信息量就越大。
 
现在我们看一下信息量的计算公式，我们首先从信息量的一些性质来说起，看信息量怎么计算才合理。有一个下忍开始了自己的职业生涯，需要一路升中忍，升上忍。事件1:该忍者顺利从下忍升为中忍，事件2:该忍者顺利从中忍升为上忍，事件3:该忍者顺利从下忍升为上忍。可以看出事件3时事件1和事件2的组合，用$P$表示概率，用$H$表示信息量，影响信息量大小的就是一个事件发生的概率，即信息量是概率的函数，即$H(P)$我们理所应当保证：
$$P_1\ast P_2=P_3$$
$$H(P_1)+H(P_2)=H(P_3)=H(P_1\ast P_2)$$
由以上公式可以看出，信息量计算公式需要满足一种从乘法到加法的转变，我们自然而言可以想到对数函数$log$，至于$log$的底我们是不很关心的，进一步观察，以概率为自变量，做对数计算得出的是负数，我们需要一个大于0的信息量（总不可能信息还会小于0吧），所以最后在公式前加上一个符号，就有了如下简单的公式：
$$H(P_i):=-log(P_i)$$
上面的公式之所以是$:=$，而不是$=$（虽然最终计算结果上这两者并没有什么不同），是因为，这是一个定义，就是说这是公式作者（哈特莱）的发明，发明成这个样子是因为这样子可以满足我们对于信息量的设想和定义，也可以保证信息学其他概念的完整性和合理性，即逻辑自洽。当计算公式是以2为底的时候，计算出来的信息量的单位是$bit$。
 
信息量的概念解释清楚之后，熵就很简单了，信息量是针对某个事件的不确定性度量，而熵是针对某个系统的不确定性度量，一个系统中可能包含了很多个事件。一个系统的熵的计算公式就是系统中所有事件信息量的概率加权求和：
$$H(system)=-\sum _{i=0}^n{p}_{i}log(p_i)$$
其中$p_i$是系统中某个事件的发生概率，系统中共有$n$个事件。信息量和熵都用了$H$表示，因为本质他们没有区别，都是不确定性的度量。
 
在机器学习中我们需要对比不同的模型，需要一个统一度量，熵就起到了这样一个作用。
 

二、相对熵（KL散度）

 
相对熵可以用来对比两个分布之间的差距，比如说我们有一个真实的分布$P$，一个我们计算得到的分布$Q$，我们想让计算结果$Q$尽可能接近$P$，怎么计算这个差距呢，$KLDivergence$ comes to recue。

 
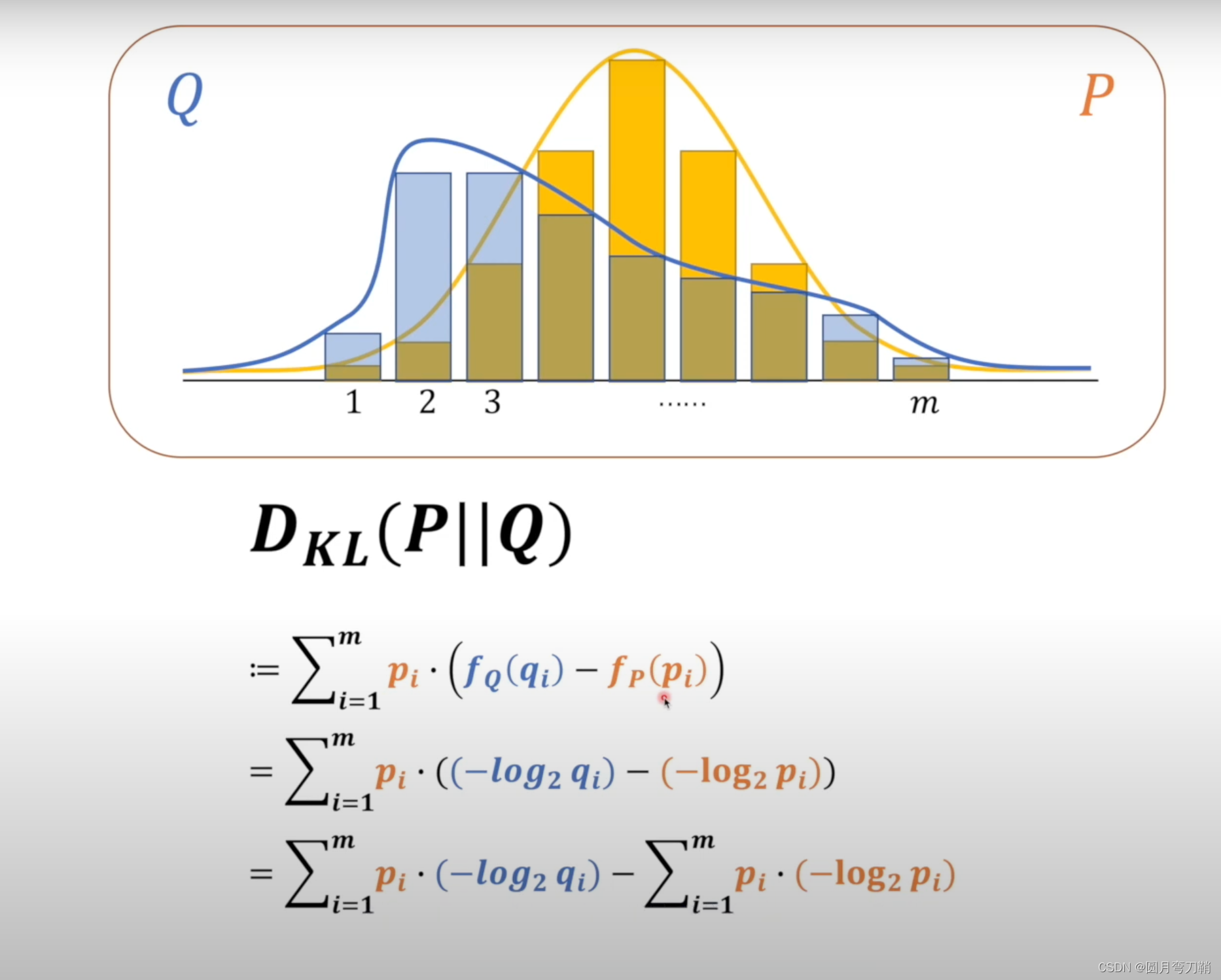
观察以上公式，最后计算结果中的第二项${\sum }_{i=1}^m{p}_i.(-lo{g}_2{p}_i)$其实就是真实分布$P$的熵，而第一项${\sum }_{i=1}^m{p}_i.(-lo{g}_2{q}_i)$就是著名的交叉熵。
 
可以看出，KL散度是不对称的，也就是说$D_{KL}(P||Q)\ne D_{KL}(Q||P)$。KL散度在任何情况下都是大于等于0的，这已经得到了证明，此处不说证明方法。
 

三、交叉熵

交叉熵被熟知是因为它经常用作分类问题的损失函数。它是KL散度计算的第一部分，由于第二部分已经固定为真实分布的熵，所以通常只取第一部分来衡量分布之间的差距。
关于交叉熵的深层意义，后续再补充。
 

四、条件熵，联合熵，互信息

 
有了上述的解释之后，之后这些衍生的概念就比较好理解：
条件熵：
$$H(X|Y)=\sum _{y\in Y}p(y)H(X|Y=y)$$
 
联合熵：
$$H(X,Y)=\sum _{y\in Y}\sum _{x\in X}-p(x,y).log(p(x,y))$$
 
互信息：
$$I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(X,Y)$$
 
它们之间的关系如下：
. . . . . . . . .