通过工作示例了解什么是向量数据库、它们如何实现 “相似性” 搜索以及它们可以在明显的 LLM 空间之外的哪些地方使用。除非你一直生活在岩石下,否则你可能听说过诸如生成式人工智能和大型语言模型(LLM)之类的术语。 除此之外,你很有可能听说过向量数据库,它为 LLMs 的查询提供上下文。 有没有想过它们是什么以及它们在明显的 LLM 领域之外有何用处? 好吧,请继续阅读以了解这项令人兴奋的新技术,构建您自己的向量数据库并思考如何在你的项目中利用它,包括但不限于 LLMs。
以值匹配为中心的搜索的局限性
首先,让我们看看到底缺少什么而引发了对不同类型数据库技术的需求。 这是与搜索数据有关。 当你在数据库中听到 “搜索” 这个词时,你可能会立即想到正常的以数值或关键字为中心的搜索,例如:
- 相等:其中 customer_id = 123
- 比较:年龄大于 25 岁
- 通配符:客户名称以 “Mc” 开头,例如 “McDonald”
有时,这些以价值为中心的搜索也相互依存,例如
其中年龄 (age) > 25 且邮政编码 (zipcode) = ‘12345’
现代数据库技术在过去几十年中不断发展,提高了此类搜索的效率,我将其称为 “以值为中心的搜索”,其中评估特定值以在查询中进行过滤。 虽然它们在许多情况下都可以工作,可以说在几乎所有与业务相关的应用程序中,但请考虑如下:
给我找一个像丽莎 (Lisa) 一样的客户
请注意所使用的过滤器:它并没有询问姓名为 “Lisa” 的客户; 只是像她这样的人,即与丽莎相似的人。 相似是什么意思? 这是一个很难回答的问题。 这不是名字,因为类似的客户可能被命名为 Alice、Bob 或 Chris。 难道是他们的年龄? 可能吧。 假设丽莎的年龄是 40 岁。40 岁的顾客最相似。 25 岁的客户相似度会降低,55 岁的客户也同样不相似。
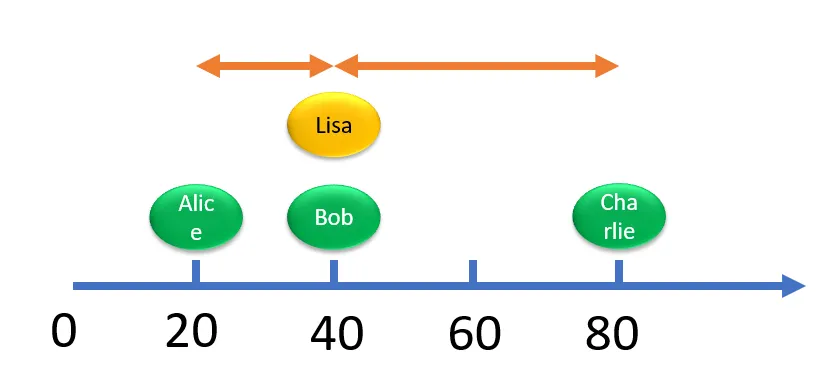
让我们思考一下。 考虑这三位顾客各自的年龄。

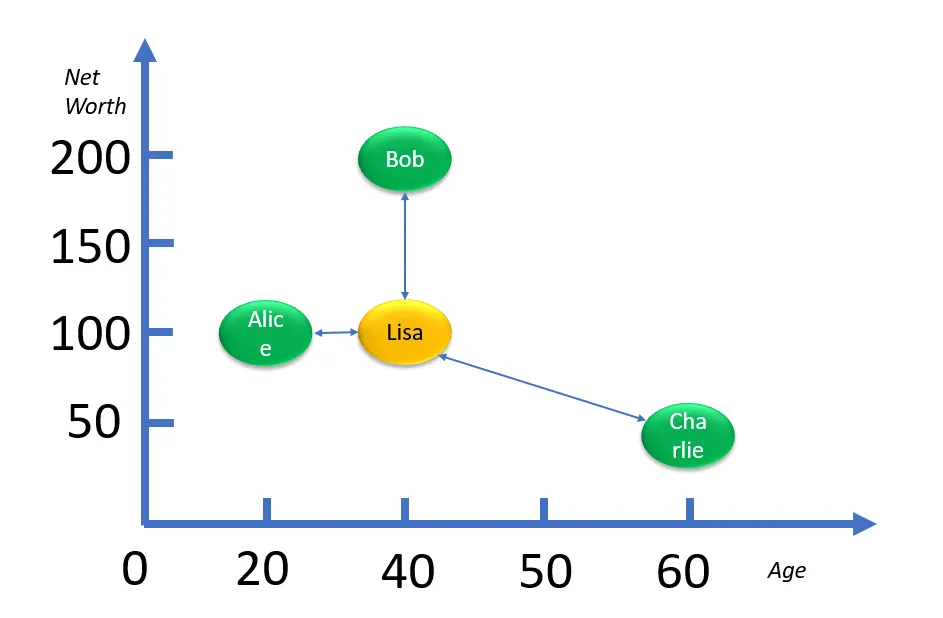
如果我们画一个图表,将 Lisa 的余额放在中间,然后绘制其他的图表,它将如下图所示。 他们的年龄与 40 岁(丽莎的年龄)的距离显示了他们距离该目标有多远。 在本例中,我们表明 Bob 最相似,Charlie 最不相似,而 Alice 更相似一些。
年龄只是客户的一方面。 在寻找 “像丽莎” 这样的人时,我们可能会想到更多的属性; 不只是一个。 其中一个属性可以是客户的净资产,如下所示,添加到原始表中:
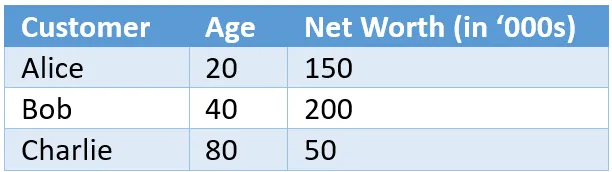
如果 Lisa 的净资产是10万,这些客户之间会有什么新的相似之处? 我们可以创建一个以年龄和净资产为两个轴的二维图表,如下图所示。
然而,由于后者以千为单位,而前者以两位数为单位,因此图表将不成比例。 为了获得相同的比例,我们需要将这些绝对值转换为一些相对值以进行比较。 年龄从 20 岁到 80 岁不等,即相差 60 岁。因此,Alice 与 Lisa 的年龄距离为 (40–20)/60 = 0.33。 同样,净资产的分布范围为 50 到 200,即 150。同样,Bob 的净资产距离为 (200–100)/150 = 0.67。
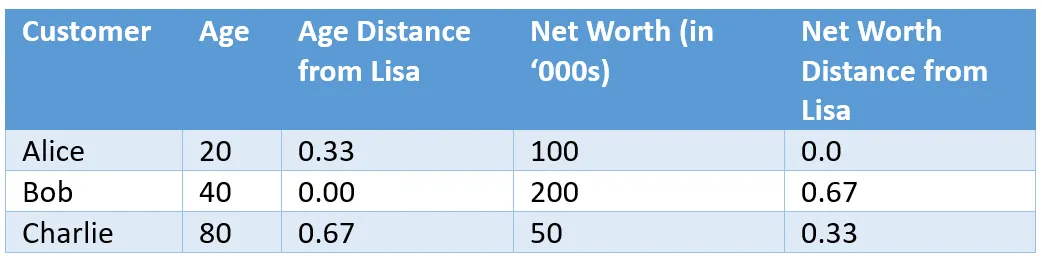
我们发现 Bon 的档案不再与丽莎 “相似”。 为了找到复合距离,我们可以在二维图上计算它们之间的距离,例如:
Composite Distance = Square Root of (Square of (Age Distance) + Square of (Net Worth Distance))使用该公式,我们计算与 Lisa 的复合距离。

我们可能会发现 Alice 距离 Lisa 的距离可能比 Bob 要近,而且和 Charlie 距离是最远。 只需添加一个维度即可显着改变相似性。 考虑添加另一个维度,例如 “孩子的数量”,使其成为 3 维图,这可能会进一步改变物体与丽莎的距离。 实际上,对象有数百个属性可供比较。 将所有这些都写在纸上是不可能的。 但希望你能了解多维空间中两点之间的距离。 距离越小,点越相似,0 表示在所有维度上完全相同。
点的属性被捕获为向量。 在上面的例子中,向量的维度将是 [Age,Net Worth]; 所以我们将按如下方式表示这些值。
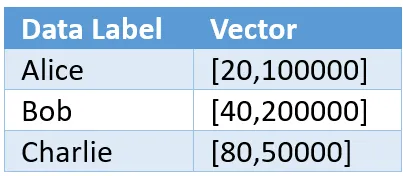
代表 Lisa 的向量是 [40,100000]。 点之间的距离通常表示为欧几里德距离,如下面二维空间的函数 d() 所示。 资料来源:维基百科。

运用 Elasticsearch 作为向量数据并计算距离
在上面,我们通过一个详细的例子描述了如何把数据转换为向量,并计算向量直接的距离。事实上,如果我们通过手动的方式来计算,就显得非常麻烦。Elasticsearch 作为全球下载量最多的向量数据库,我们可以很方便地利用它来帮我们进行计算向量之间的相似性。下面,我们来通过 Elasticsearch 来实现向量之间的相似性。
首先,我们为向量的索引定义一个 mapping:
PUT my-index
{
"mappings": {
"properties": {
"my_vector": {
"type": "dense_vector",
"dims": 2,
"similarity": "l2_norm"
},
"name" : {
"type" : "keyword"
}
}
}
}请注意,在上面,我们定义了一个叫做 dense_vector 的数据类型。这个就是我们的向量数据类型。它的维度为 2。我们可以详细参考 Elastic 官方文档来了解这个数据类型。my_vector 的相似性,我们使用 l2_norm 来定义 similarity,它表明是欧几里得距离。请详细参阅文档。
我们通过如下的命令来写入数据到 Elasticsearch:
POST my-index/_bulk?refresh=true
{ "index" : { "_id" : "1" } }
{ "name" : "Alice", "my_vector": [20,100000] }
{ "index" : { "_id" : "2" } }
{ "name" : "Bob", "my_vector": [40,200000] }
{ "index" : {"_id" : "3" } }
{ "name" : "Charlie", "my_vector": [80,50000] }我们可以通过如下的命令来查看写入的数据:
GET my_index/_search?filter_path=**.hits上面的命令返回的响应为:
"hits": {
"hits": [
{
"_index": "my_index",
"_id": "1",
"_score": 1,
"_source": {
"name": "Alice",
"my_vector": [
20,
100000
]
}
},
{
"_index": "my_index",
"_id": "2",
"_score": 1,
"_source": {
"name": "Bob",
"my_vector": [
40,
200000
]
}
},
{
"_index": "my_index",
"_id": "3",
"_score": 1,
"_source": {
"name": "Charlie",
"my_vector": [
80,
50000
]
}
}
]
}
}我们可以通过 Elasticsearch 来计算我们搜索对象 Lisa 的距离。搜索的结果将返回在我们的向量数据库中最近的向量。它们是按照距离的大小进行排序的。在上面的向量中,我们想找到一个最相近的 Lisa,而它的向量为 [40, 100000]。我们可以通过如下的方法来搜索我们的向量:
接下来,我们使用 Elasticsearch 的 knn search 端点来进行搜索:
POST my-index/_search?filter_path=**.hits
{
"knn": {
"field": "my_vector",
"query_vector": [40, 100000],
"k": 10,
"num_candidates": 100
}
}上面的搜索结果是:
{
"hits": {
"hits": [
{
"_index": "my-index",
"_id": "1",
"_score": 0.0024937657,
"_source": {
"name": "Alice",
"my_vector": [
20,
100000
]
}
},
{
"_index": "my-index",
"_id": "3",
"_score": 3.9999976e-10,
"_source": {
"name": "Charlie",
"my_vector": [
80,
50000
]
}
},
{
"_index": "my-index",
"_id": "2",
"_score": 1e-10,
"_source": {
"name": "Bob",
"my_vector": [
40,
200000
]
}
}
]
}如上所示,我们看到的结果是 Alice 排名是第一的,而紧随其后的是 Charlie。而我们之前认为的 Bob 是排在最后的一个。Bob 的距离是最远的,这个和之前的推送方法有一定的误差,比如相对计算的方法不同。
更多有关 Elasticsearch 向量搜索的内容,请详细阅读文章 “AI”。