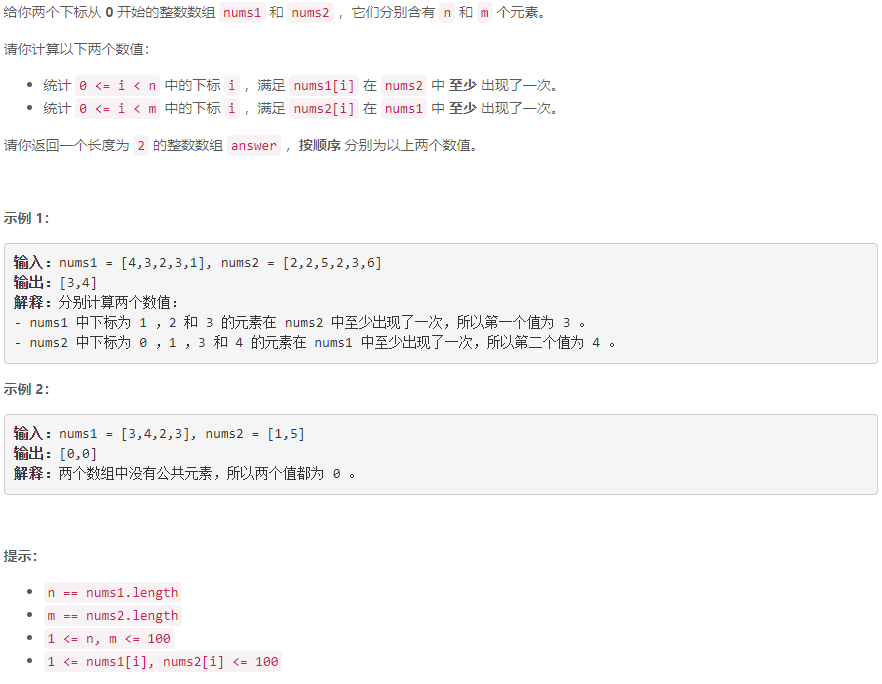
模拟

class Solution {
public:
    vector<int> findIntersectionValues(vector<int> &nums1, vector<int> &nums2) {
        unordered_set<int> s1(nums1.begin(), nums1.end()), s2(nums2.begin(), nums2.end());
        vector<int> res(2);
        for (auto x: nums1)
            if (s2.count(x))
                res[0]++;
        for (auto x: nums2)
            if (s1.count(x))
                res[1]++;
        return res;
    }
};

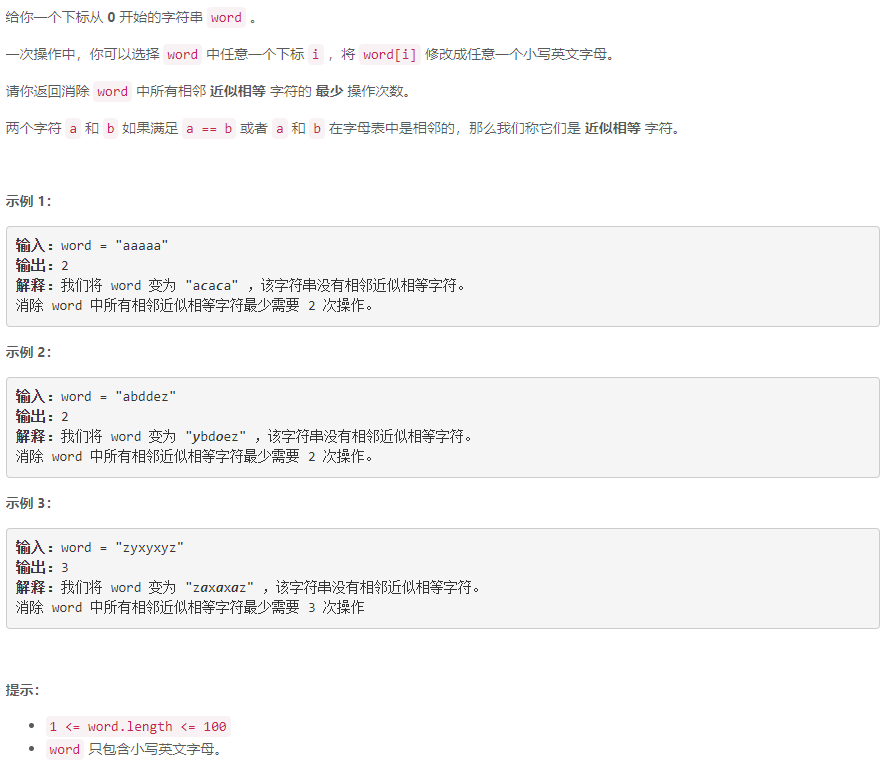
动态规划：设 $p[i][j]$ 为将 $word[0,i]$ 修改为末位为 $j$ 的不含相邻近似相等字符串的最少操作数，枚举可能的 $word[i-1]$ 进行状态转移

class Solution {
public:
    int removeAlmostEqualCharacters(string word) {
        int n = word.size();
        int p[n][26];
        for (int j = 0; j < 26; j++)
            p[0][j] = 1;
        p[0][word[0] - 'a'] = 0;
        for (int i = 1; i < n; i++)
            for (int j = 0; j < 26; j++) {
                p[i][j] = INT32_MAX;
                for (int pre = 0; pre < 26; pre++)
                    if (abs(j - pre) > 1)
                        p[i][j] = min(p[i][j], p[i - 1][pre] + (word[i] - 'a' == j ? 0 : 1));
            }
        int res = INT32_MAX;
        for (int j = 0; j < 26; j++)
            res = min(res, p[n - 1][j]);
        return res;
    }
};

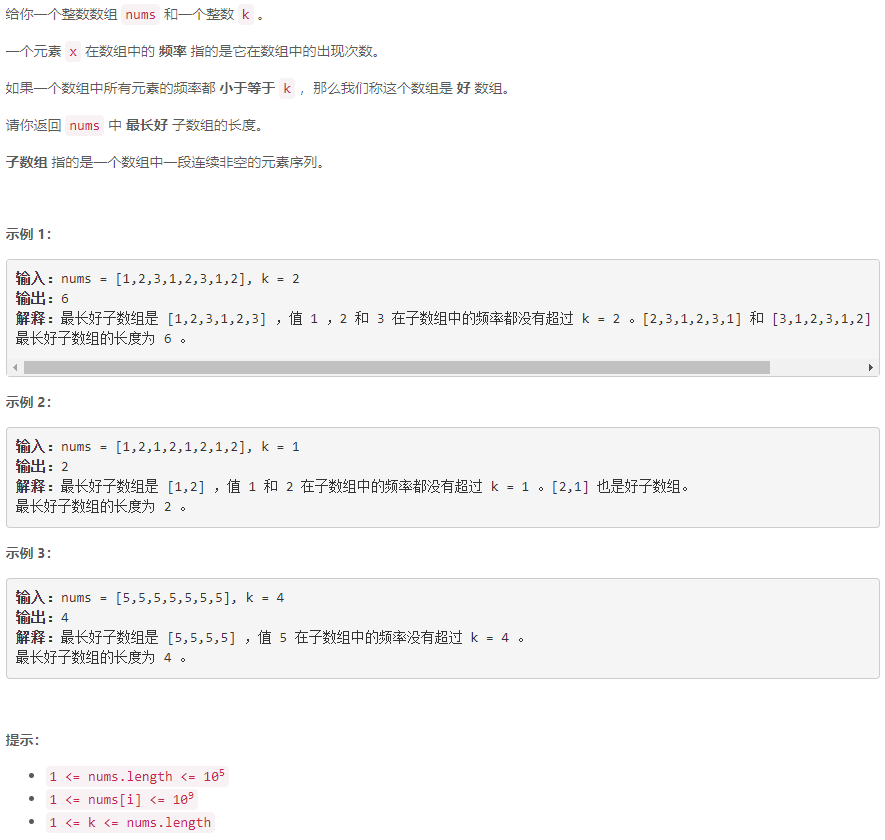
滑动窗口+哈希：哈希表记录滑动窗口内数的频率，枚举滑动窗口的左边界，尽可能移动滑动窗口的右边界

class Solution {
public:
    int maxSubarrayLength(vector<int> &nums, int k) {
        int n = nums.size();
        int res = 0;
        unordered_map<int, int> f;
        for (int l = 0, r = -1; l < n; f[nums[l++]]--) {
            while (r + 1 < n && f[nums[r + 1]] + 1 <= k)//滑窗左边界固定时，尽可能移动右边界
                f[nums[++r]]++;
            res = max(res, r - l + 1);
        }
        return res;
    }
};

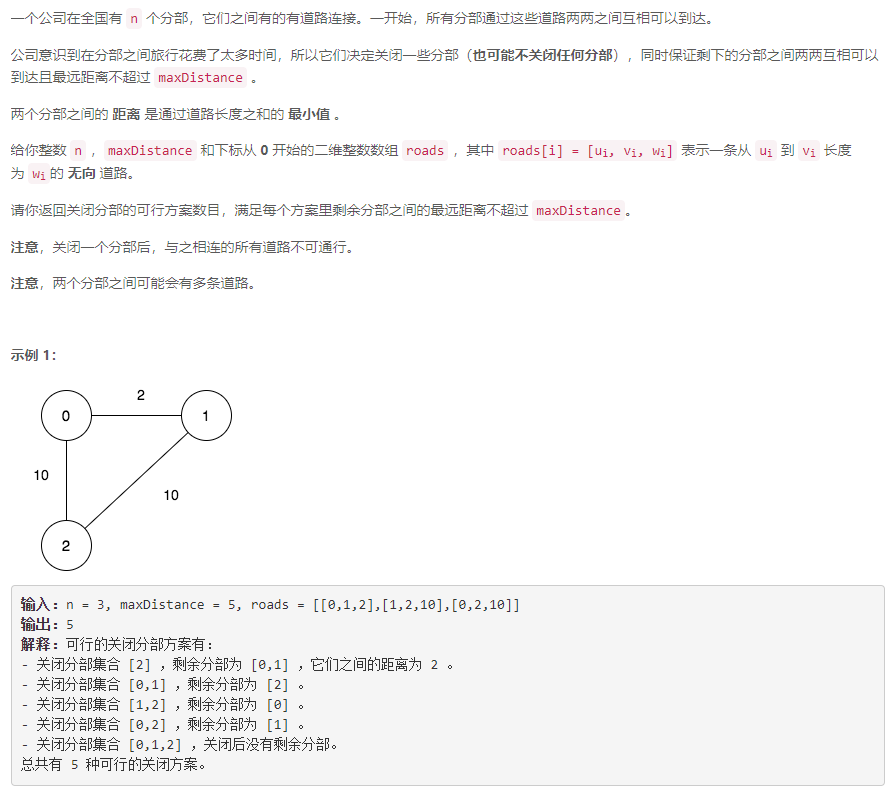
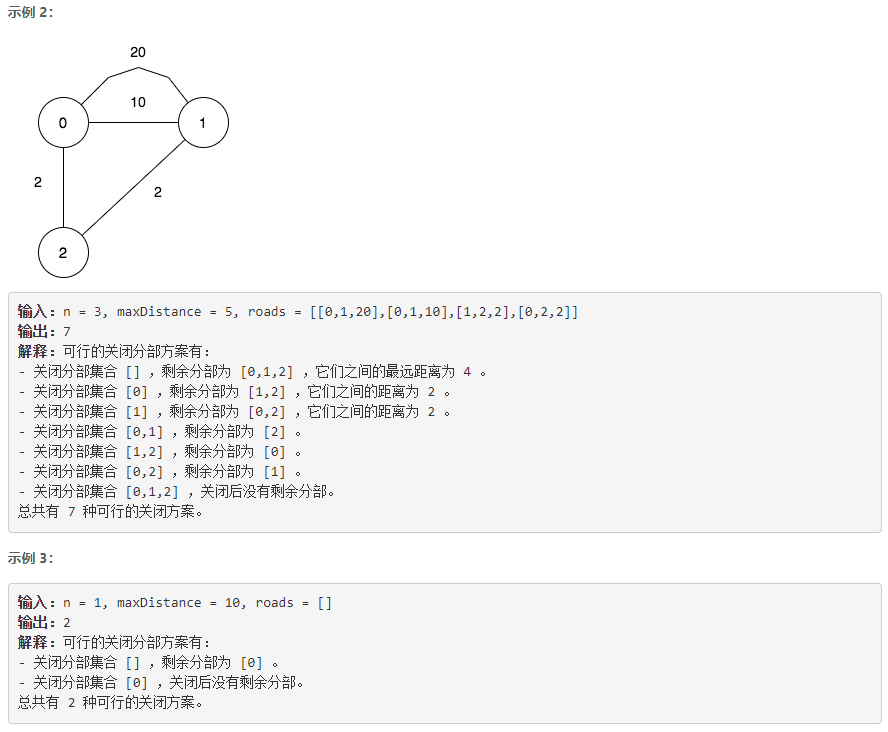
枚举：枚举可能的关闭分部集合，然后在当前关闭情况下跑多源最短路算法，然后判断最大的最短路是否不超过 $maxDistance$

class Solution {
public:
    inline int get_bit(int mask, int loc) { return mask >> loc & 1; }//返回mask二进制表示的第loc位

    int pop_cnt(int mask) {//返回mask二进制表示中1的个数
        int res = 0;
        for (; mask; mask >>= 1)
            if (mask & 1)
                res++;
        return res;
    }

    int numberOfSets(int n, int maxDistance, vector<vector<int>> &roads) {
        int inf = INT32_MAX;
        vector<vector<int>> g(n, vector<int>(n, inf));
        for (auto &e: roads) {
            g[e[0]][e[1]] = min(g[e[0]][e[1]], e[2]);
            g[e[1]][e[0]] = g[e[0]][e[1]];
        }
        int res = 0;
        for (int mask = 0; mask < (1 << n); mask++) {//枚举关闭分部集合:mask二进制中第i位为0表示第i个分部关闭
            auto t = g;
            for (int k = 0; k < n; k++)
                if (get_bit(mask, k))
                    for (int i = 0; i < n; i++)
                        if (get_bit(mask, i))
                            for (int j = 0; j < n; j++)
                                if (get_bit(mask, j))
                                    if (t[i][k] != inf && t[k][j] != inf)
                                        t[i][j] = min(t[i][j], t[i][k] + t[k][j]);
            int mx = 0;//最大的最短路
            for (int i = 0; i < n; i++)
                if (get_bit(mask, i))
                    for (int j = 0; j < n; j++)
                        if (j != i && get_bit(mask, j))
                            mx = max(mx, t[i][j]);
            if (mx <= maxDistance)
                res++;
        }
        return res;
    }
};