前言：在学习二叉树的时候我们基本上已经了解过二叉树的三种遍历，对于这三种遍历，我们采用递归的思路，很简单的就能实现，那么如何用迭代的方法去解决问题？

我们首先来看第一个：

前序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）

前序遍历就是以 根 左子树 右子树的顺序遍历二叉树。呢么如何用得带去解决问题呢？

首先我们知道函数递归就是函数一层层的调用自己，本质上是以一种先进后退的思路，而这与栈的特性一致，因此函数递归，我们可以用调用堆栈来看，就是栈的思路。

现在我们解决问题，既然不用递归，但还是可以用到解决问题的本质思路，就是用栈去解决问题：

例图：

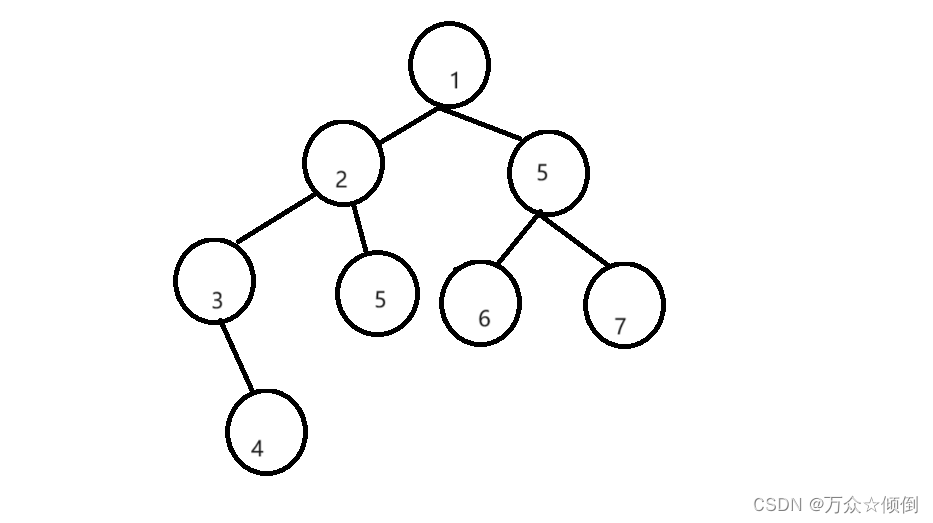
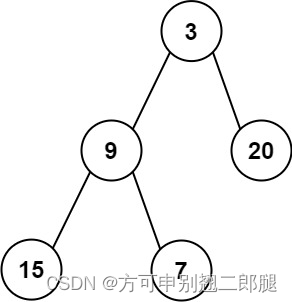
 我们就用这个图做演示：

大致解题思路：由于二叉树遍历一直往下走，无法回头，我们需要提供一个栈，假设我们每次先遍历左子树，每次遍历的时候，将我们需要往回遍历的节点放入栈中（往回遍历的节点就是拥有右子树的系点），在遍历完左节点后，此时回退上一个节点，看他的右子树是否为空。

且我们的整个循环的条件中 栈是否为空 就决定是否继续遍历这一个二叉树。

首先前序遍历的顺序 是根  左子树 右子树 。其次，对于二叉树，解决了整个左子树的遍历。那么整个右子树的遍历，也是与之相同的，也就是我们再解决问题时就只针对一个子树，这里我们就以遍历整个左子树为主，实现对整个树的遍历。且题目要求返回数组，因此我们是遍历插入数据。

由于我们无法知道某个左节点的右节点是否为空，所以开始我们先将所有左节点入栈：

第一步操作：

首先要遍历根，也就是从1开始，不为空，放入数组，并入栈，在看它的左，2不为空，放入数组，并入栈，再看它的左，3，不为空，放入数组并入栈。我们就完成了第一步，但是对于最后一个最左节点（它可能是一个子树的根，他也有可能是子树的左节点）。

第二步操作：

从这里开始，我们就要开始判断是否出栈，此时获取当前栈顶元素，3节点，再出栈。（此时栈不为空）

   若3节点无右节点，此时根已经遍历完了，现在轮到左子树了，而3此时是作为一个子树的左节点，并且是遍历顺序左子树中的第一个节点，之后出栈，看节点2的右子树是否存在。

   若3节点有右节点（右子树），比如我们这里就是节点4,3节点就往右子树走，按照前序遍历顺序，我们该将此节点数据放入数组中，因此以该节点为开始，继续第一步操作，将该右节点（也有可能是右子树）,按照先把左节点入栈，入数组，在判断右子树情况来出栈。

第三步操作：

其实我们的前序遍历已经实现，可能有人还觉得还没完成，因为右子树还没处理，实际上当我们回退二叉树,也就是出栈的时候，出到最后一个元素，也就是真正的根节点时，栈不为空，循环还没结束，会继续判断当前节点的右子树。

代码实现：

vector<int> preorderTraversal(TreeNode* root) {
    
    //用来返回遍历结果的数组
    vector<int> v;
    
    //用栈来回退我们二叉树
    stack<TreeNode*> t;
    
    TreeNode*node=root;
    //当节点为空或者栈不为空的时候循环继续
    while(node||!t.empty())
    {
       //第一步将左边的节点一次放入数组并入栈 
        while(node)
        {
            v.push_back(node->val);
            t.push(node);
            node=node->left;
        }
        //从该位置开始判断是否要出栈
        node=t.top();
        t.pop();
        if(node->right==nullptr)
         {
            node=nullptr;//直接为空，继续循环进入到出栈操作
         }else
         {
           node=node->right;
         }      
    }
     return v;
    }

中序遍历

中序遍历 的顺序是 左节点 根 右子树 。与前序的插入思想不太一样，不过还是利用栈来回到上一个节点。前序遍历时，其实是有点巧合，因为根节点与左节点连续，我们是直接将左节点一个个入栈后，直接放入数组，因为顺序是从根节点开始，且根节点下来就是左节点，因此插入顺序与我们的直接将左节点插入的顺序一致。

但对于中序和后序遍历，都是先从左节点开始的，因此，从根开始，我们是先将之后的左节点一个个入栈，这里就不能再放数组了，直到最左节点时，根据我们的的遍历顺序，下来时根节点，再来判断。具体分析如下：

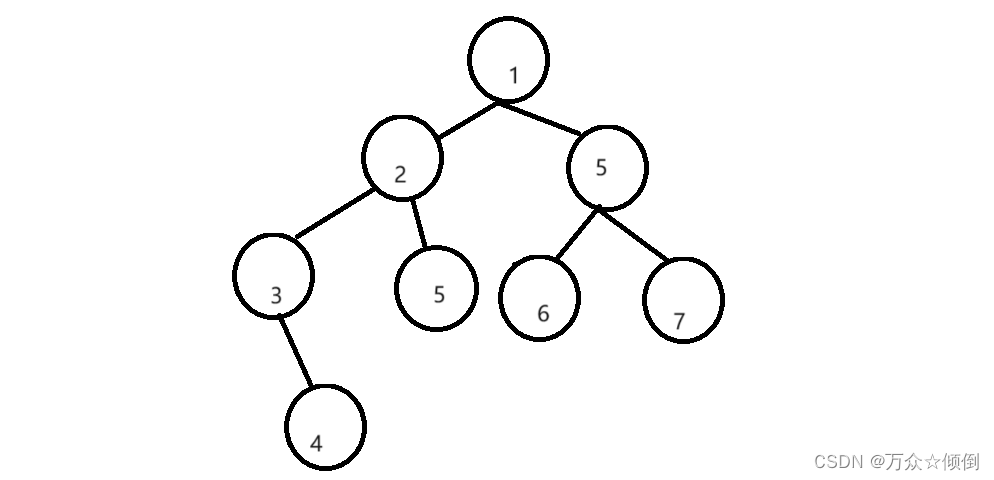
还是以这张图为例：

第一步：

刚开始我们还是直接以根为开始，将它的一个个左节点入栈，此时栈中为3，2，1。

第二步：

从这里开始，就需要判断是否出栈，是否插入数组，因此从这里开始，还是先获取栈顶元素，在出栈，当前位置就是节点3，之后就是判断3节点是否具有右子树。

若没有右子树，那么3就是第一个左节点，放入数组，之后回退到上一个节点2，继续判断。

若有右子树，此时节点3是一个根，不能放入数组，我们继续走到节点4，以4节点为开始，与前序遍历一样，执行第一步的操作进行入栈，之后在判断。

直到回退到根节点，此时进行右子树的遍历。

代码如下：

  vector<int> inorderTraversal(TreeNode* root) {
    vector<int> v;
    stack<TreeNode*> t;
    TreeNode* prev=nullptr;
    while(root||!t.empty())
    {
        while(root)
        {
         if(root)
         {
            t.push(root);
         }
         root=root->left;
        }
        root=t.top();
        t.pop();      

        //为空先插左节点
        v.push_back(root->val);
        if(root->right==nullptr)
        {
          root=nullptr;
        }else
        {
          root=root->right;
        }
            
    }
     return v;
    }

 后序遍历

后序遍历的思路与中序遍历有些许一样，但对于情况的判断更加复杂。

因为后序的遍历顺序为 左子树  右子树 根，育贤婿一样，我们还是从根节点开始，入栈左子树的所有左节点，直到最左节点，还是要进行判断。具体分析如下：

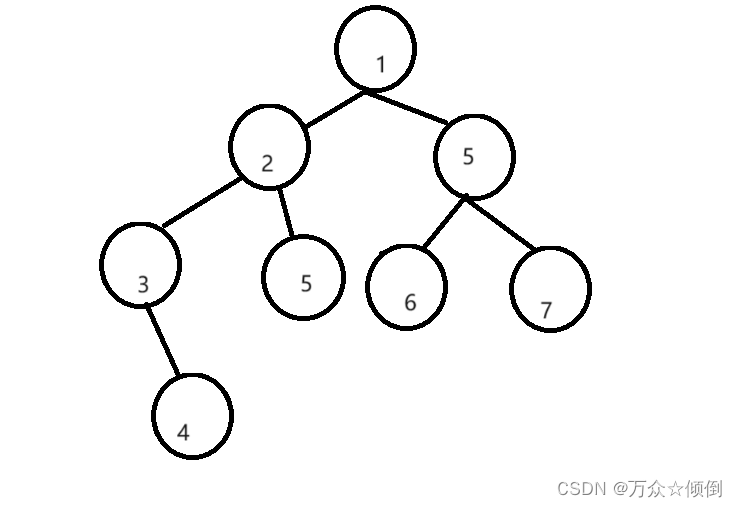
 还是一这张图为例：

第一步：

依然是将左子树的所有的左节点依次入栈， 1入，2入，3入，此时到了节点3。

第二步：

从节点3开始判断是否要回退，因此获取栈顶节点为3，出栈，当前节点为3。

若3没有右节点，此时我们就是左节点，我们就可以将3放入数组，之后回退到节点2。

若3的右节点存在，此时的操作是将该节点再次重新入栈（因为下一个右节点（右子树）插入完才轮到我），之后当前节点走到这个右节点，循环回到第一步，继续入栈。

在这里有重要的一点：

第一点：与之前两种遍历一样，我们需要从当前节点回退到上个节点的方法是将指针置空，之后重新赋值为栈顶元素的节点。

其次除了叶子节点容易判断插入，如果上一次插入的节点，是当前节点的右节点，则就需要放入数组里，即 先插的左， 之后插的右，根节点需要判断，当前节点的右节点是上一次插入的节点就说明是根，插入数组。

源码：

vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*>s;
        vector<int> ret;
        TreeNode*prev=nullptr;
     
        while(root||!s.empty())
        {
            //先找所有的左节点
            while(root)
            { 
                s.push(root);
                root=root->left;
            }
            //倒退判断这些节点的右节点，直到最后根节点，在判断右子树
            root=s.top(); 
            s.pop();
            if(root->right==nullptr ||root->right==prev) 
            {
                ret.push_back(root->val);
                prev=root;
                root=nullptr;

            }else
            {
                //若右子树不为空，继续入栈
                 s.push(root);
                root=root->right;
            }
        }
     return ret;
    }