文章目录
- 上一篇
- 启发式搜索
- 与或图搜索
- 博弈
- 下一篇
上一篇
人工智能原理复习–搜索策略(一)
启发式搜索
提高一般图搜索效率的关键是优化OPEN表中节点的排序方式
最理想的情况是每次排序OPEN表表首n总在解答路径上
全局排序–对OPEN表中的所有节点进行排序(A算法,A*算法)
局部排序–仅对新扩展出来的子节点排序(爬山法)
A算法
基本思想:
设计体现启发式知识的评价函数
f
(
n
)
f(n)
f(n)指导OPEN表中带扩展节点的排序。
评价函数:
f
(
n
)
=
g
(
n
)
+
h
(
n
)
f(n) = g(n) + h(n)
f(n)=g(n)+h(n)
n – 搜索图G中的节点
f(n) – G中从初始状态节点s,经由节点n到达目标节点
n
g
n_g
ng, 估计的最小代价
g(n) – G中从s到n,目前实际的路径代价
h(n) – 从n到
n
g
n_g
ng, 估计的最小代价
h(n)称为启发式函数
与一般图搜索顺序类似
但是在扩展n的节点时对每个子节点
n
i
n_i
ni计算
f
(
n
,
n
i
)
=
g
(
n
,
n
i
)
+
h
(
n
i
)
f(n, n_i) = g(n, n_i) + h(n_i)
f(n,ni)=g(n,ni)+h(ni)
然后适当标记修改指针,排序OPEN表

实现启发式搜索应考虑的关键因素:
- 搜索算法的可采纳性
- 启发式函数h(n)的强弱及其影响
若一个搜索算法总能找到最短(代价最小)的解答路径,则称该状态空间的搜索算法具有可采纳性,也叫最优性。
宽度优先搜索算法是可采纳的,只是搜索效率不高。
A算法是可采纳的
.
A
∗
算法
A^*算法
A∗算法
如果A算法是可采纳的则
f
∗
(
n
)
=
g
∗
(
n
)
+
h
∗
(
n
)
f^*(n) = g^*(n) + h^*(n)
f∗(n)=g∗(n)+h∗(n)
*代表实际的最短路径
理想情况下:
g
(
n
)
=
g
∗
(
n
)
、
h
(
n
)
=
h
∗
(
n
)
g(n) = g^*(n)、h(n) = h^*(n)
g(n)=g∗(n)、h(n)=h∗(n)
每次搜索过程中不扩展任何无关结点
而实际情况下g(n)容易在已经生成搜索树中计算出来,但是h(n)具有未知性,只能尽可能靠近 h ∗ ( n ) h^*(n) h∗(n)
因此可以得出
A
∗
算法定义
A^*算法定义
A∗算法定义:
在A算法中,规定
h
(
n
)
<
=
h
∗
(
n
)
h(n) <= h^*(n)
h(n)<=h∗(n)
A算法中最优秀的就是
A
∗
A^*
A∗算法
而 h(n)接近 h ∗ ( n ) h^*(n) h∗(n)的程度–是衡量启发式函数的强弱
- h ( n ) < h ∗ ( n ) h(n) < h^*(n) h(n)<h∗(n)且差距过大,排序误差较大,产生更大的搜索图,无用节点更多
- h ( n ) > h ∗ ( n ) h(n) > h^*(n) h(n)>h∗(n)且h(n)过强,A算法失去可采纳性,不能确保找到最短路径
- h ( n ) = h ∗ ( n ) h(n) = h^*(n) h(n)=h∗(n)可以确保生成最小的搜素图,找到最短路径
因此 A ∗ A^* A∗算法就是在 h ( n ) < = h ∗ ( n ) h(n) <= h^*(n) h(n)<=h∗(n)的条件下,越大越好。
若h(n) = 0
⇒
\Rightarrow
⇒ BFS
若g(n) = 0
⇒
\Rightarrow
⇒ DFS
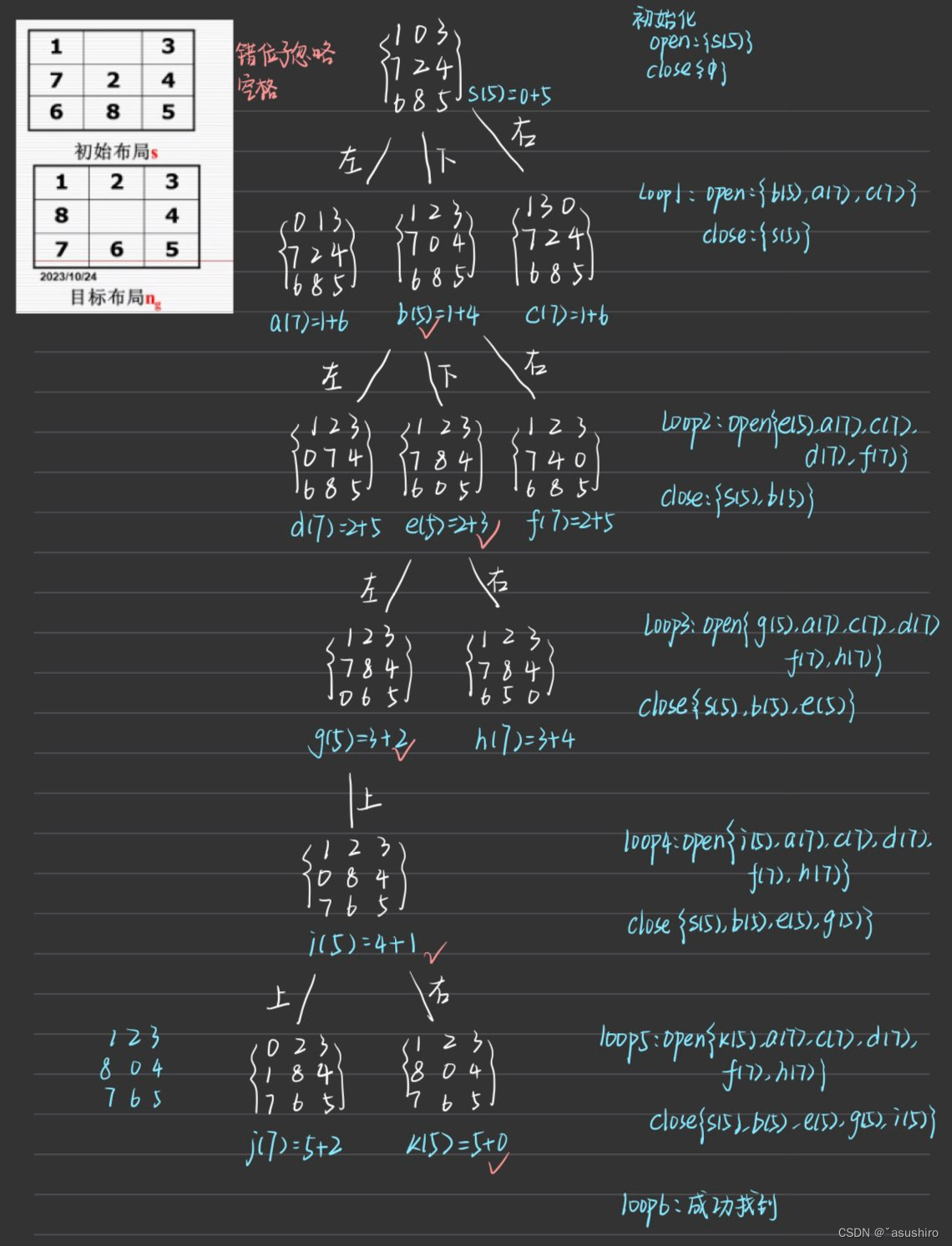
通过模拟过程,和算法设计与分析的堆优化的分支界限法相似
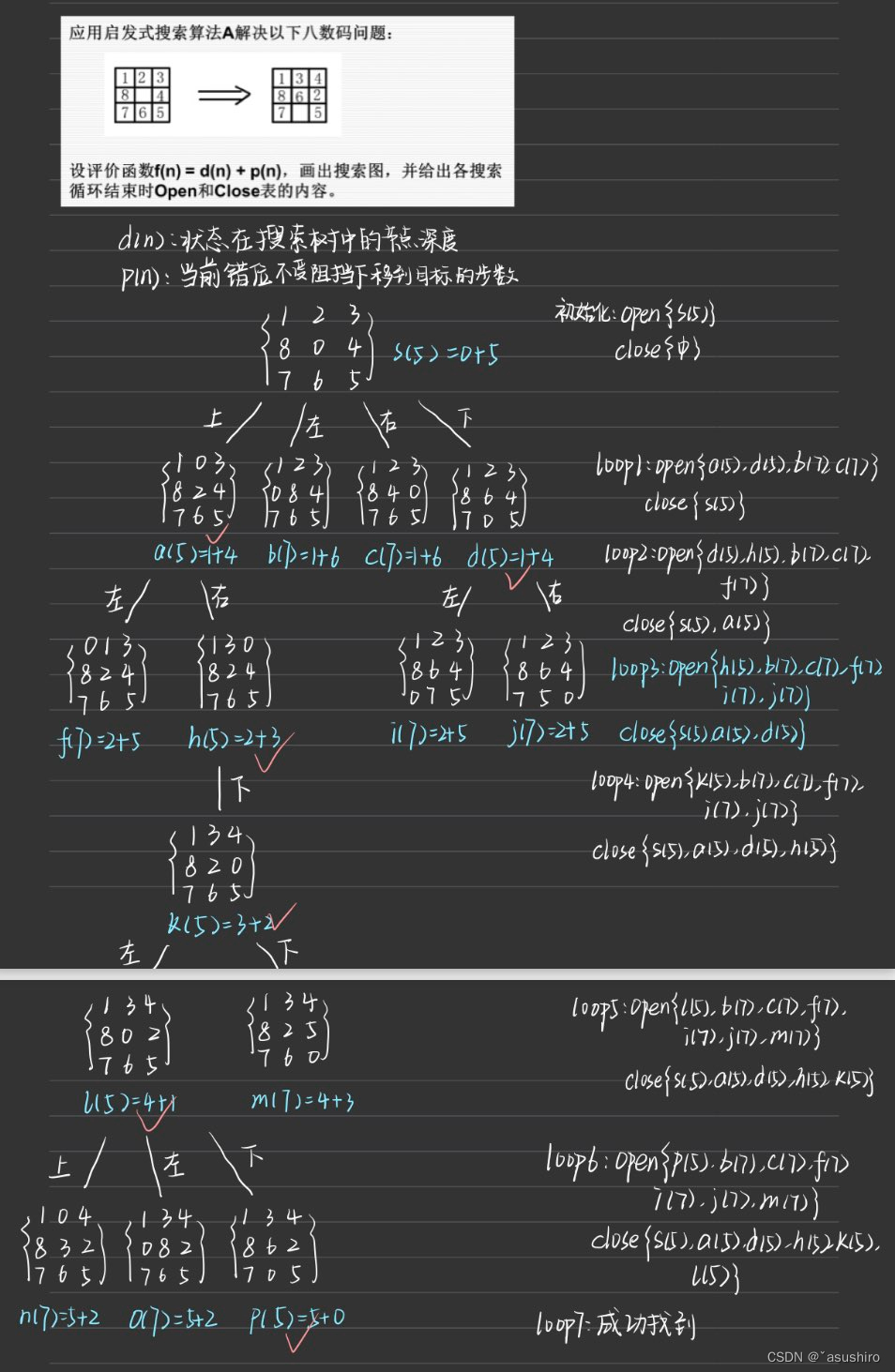
close表就是已经访问过的状态,open表就是待访问的状态,而评估函数就是找出下一个最先访问的状态

定义状态空间,
定义对应状态的h(n)


为更有效地搜索解答,可使用评价函数
f
(
n
)
=
g
(
n
)
+
w
∗
h
(
n
)
f(n) = g(n) + w*h(n)
f(n)=g(n)+w∗h(n),添加一个加权
在搜索图的浅层(上部),可让w取较大值,使得搜索加速向纵深方向搜索
当搜索到较深的层次时,再让
w
w
w 取较小值, 保证
w
h
(
n
)
<
=
h
∗
(
n
)
wh(n) <= h^*(n)
wh(n)<=h∗(n)的情况下,在横向方向发展,寻找较短的解答路径
迭代加深
A
∗
A^*
A∗算法
由于
A
∗
A^*
A∗算法会将节点全部保存在内存中,所以
A
∗
A^*
A∗算法困在空间问题
因此有了迭代加深
A
∗
A^*
A∗算法
I
D
A
∗
IDA^*
IDA∗算法
但是不满足最优性和完备性
它以深度优先的方式在有限制的深度内搜索目标节点,在每个深度上,该算法在每个深度上都会检查节点是否出现如果出现则停止,否则深度加一继续搜索。启发函数用作深度的限制, 而不是选择扩展结点的排序。
特点:由于 A ∗ A^* A∗算法需要指数级的存储空间,没有深度限制,而 I D A ∗ IDA^* IDA∗算法可以节省大量内存。当启发式函数是最优的时候, I D A ∗ IDA^* IDA∗算法和 A ∗ A^* A∗算法扩展相同的结点,并且可以找到最优路径。
与或图搜索
问题归约:是将复杂问题转换成若干需要同时处理的较为简单的子问题后再加以分别求解,只有子问题全部解决时,问题才算解决。问题的解答由子问题的解答联合构成。
实质就是,将目标逆向推理分解成一个个子问题,直至最后把初始问题归约为一个平凡的本原问题集合。
运用问题归约策略得到的状态空间图称为与或图。
表示:
用圆弧将几条节点间关联弧连接起来,子问题全部解决才能导致原问题解决。
或关系
→
\rightarrow
→解决其中一个或关系就能解决上层问题
与或图基本概念:
- K-连接:父节点与K个子节点连接,子节点之间是与关系。
一个父节点可以有多个K-连接(与关系)
K-连接之间是或关系 - 解图:解答路径不复存在,取而代之的是广义的接路径----解图, 解图是纯粹的与图,节点之间不存在或关系。
- 终节点:能用于联合表示目标状态的节点
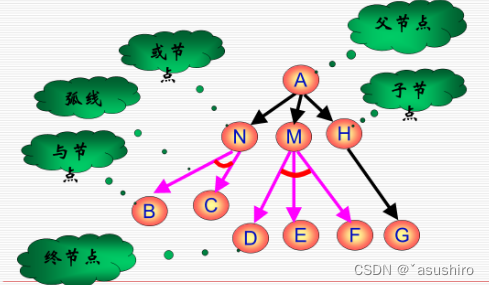
-
解图的生成:从根节点选K-连接,然后从子节点再选择K-连接直到所有K-节点都指向终节点为止。存在或关系可能搜索到多个解图。
-
解图的代价:
令K-连接的代价就是K
则代价 C ( n ) = K + C ( n 1 ) + C ( n 2 ) + . . . + C ( n k ) C(n) = K + C(n_1) + C(n_2) + ...+ C(n_k) C(n)=K+C(n1)+C(n2)+...+C(nk) -
能解节点:
终节点是能解节点,若K-连接的子节点都是能解节点则这个父节点也是能解节点。 -
不能解节点:
非终节点是不能解节点,若K-连接至少连接一个不能解节点则父节点是不能解节点
AO*算法



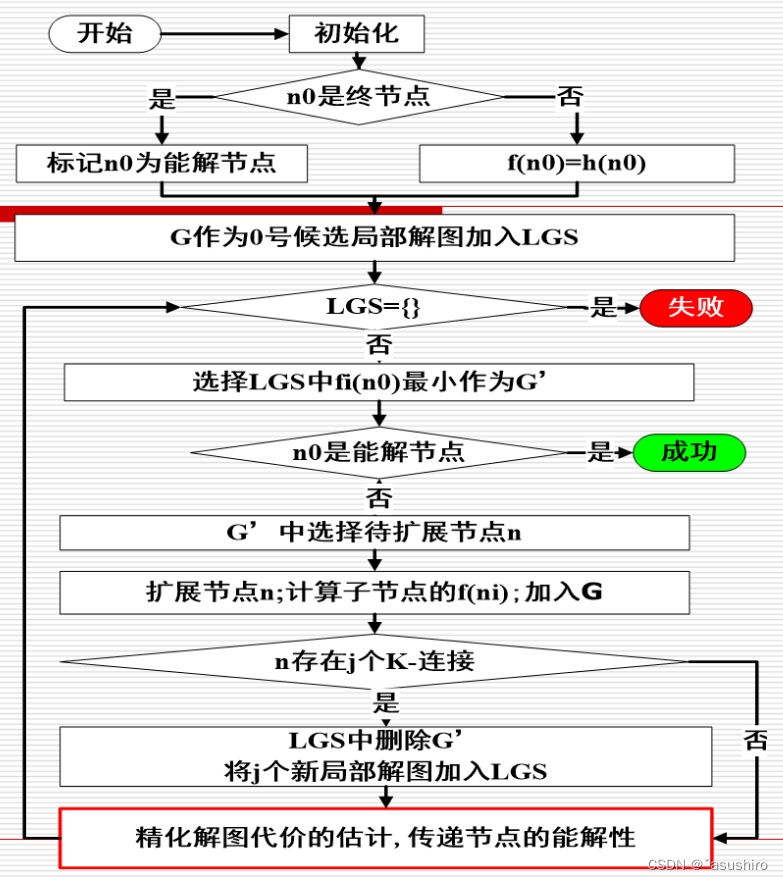
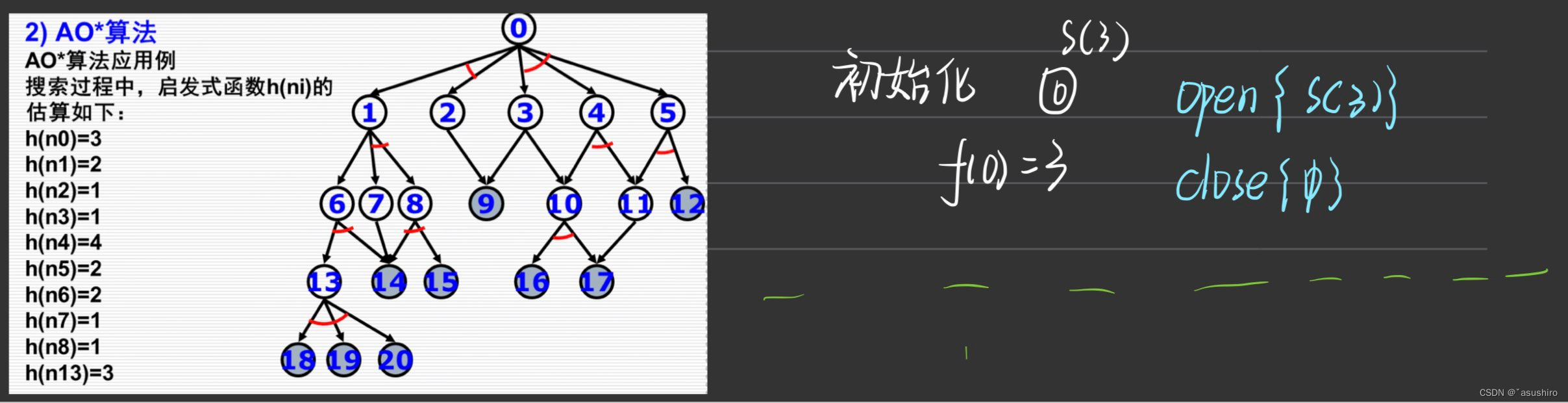

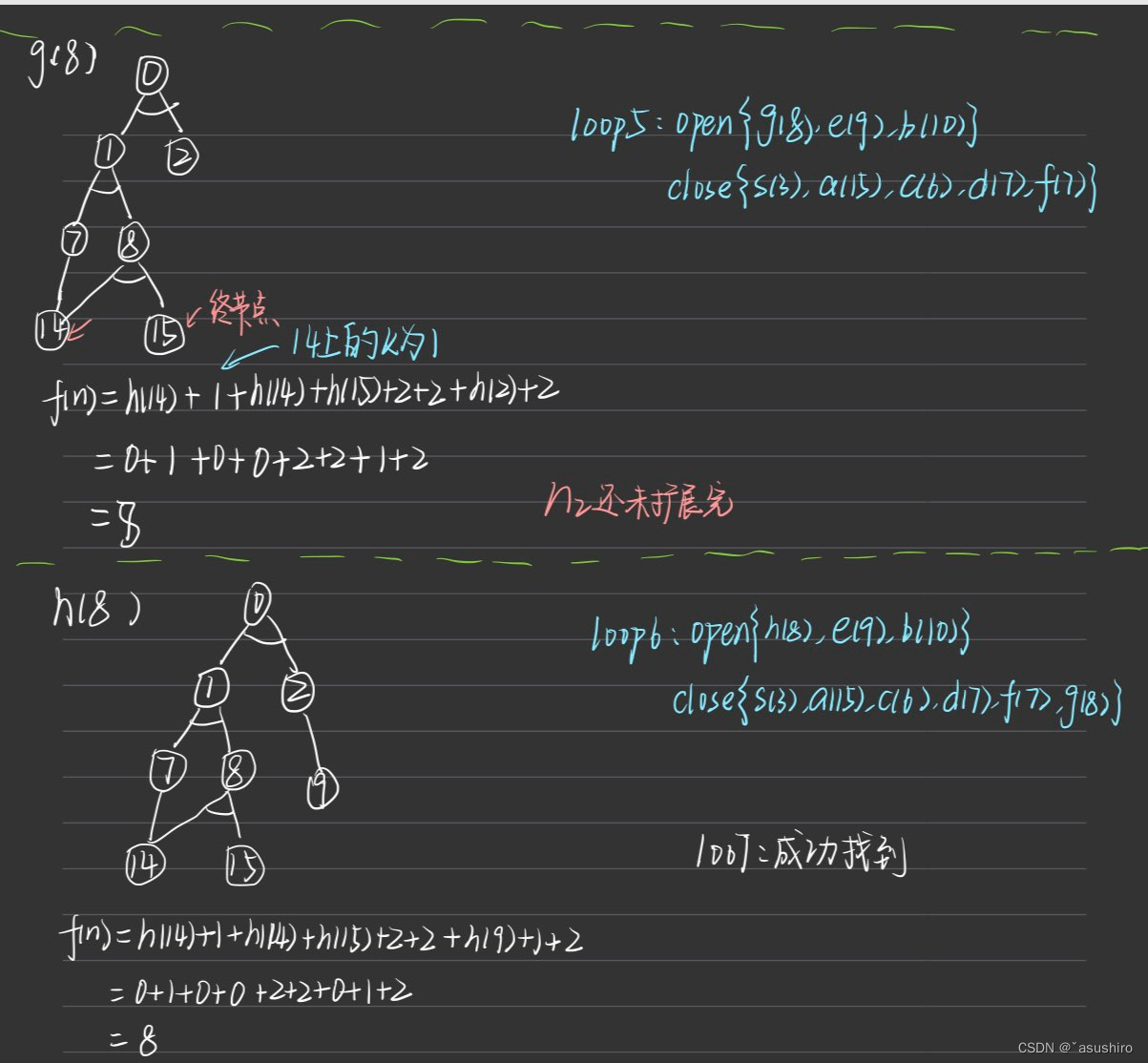
博弈
博弈树的特点:
- 博弈的初始状态是初始节点
- 博弈树的“与”节点和“或”节点是逐层交替出现的
- 整个博弈过程始终站在某一方的立场,让自己获胜的为可解节点,让对方获胜的都是不可解节点
极大极小过程
考虑对弈若干不之后从可能的走法中选一步相对好的走法来走,即在有限的搜索深度范围内进行求解。
需要定义一个静态评估函数f,对棋取台式进行分析。
双方定义:
MAX方:有利于,f( p)取正值
MIN方:有利于,f( p)取负值
均衡时f§为0,p代表棋局。
基本思想:
- 当轮到MIN走步的节点时(取与时),MAX应考虑最坏情况( f ( p ) f(p) f(p)取极小值)
- 当轮到MAX走步的节点时(取或时),MAX应考虑最好的情况( f ( p ) f(p) f(p)取极大值)
- 评价使用1、 2的极值进行推出评估函数的值
过程:
定义博弈树的层数(往后考虑几步),设定静态评估函数(找到最优步),形成博弈树
优点:
- 确保最优解: 极大极小过程的一个主要优势是能够确保在有限的博弈情境中找到最优解,即使是在较为复杂的游戏中也能找到最优解决方案。
- 理论上的保证: 在完全信息和有限博弈的情况下,这个算法可以保证找到一个最优解,这是一种理论上的保证。
- 广泛适用性: 这种算法不仅限于特定类型的游戏或情景,可以应用于各种类型的博弈,从棋类游戏到经济决策等。
缺点:
- 计算复杂度高: 在某些情况下,特别是在博弈树非常庞大的情况下,极大极小过程需要大量的计算资源和时间,可能会变得不切实际,效率较低。
- 只适用于完全信息博弈: 这个算法假设所有的信息都是完全可见的,而在现实生活中很多情况下信息并不完整,这限制了它在实际应用中的适用性。
α − β \alpha-\beta α−β过程
由于极大极小过程生成博弈树会生成规定深度的所有节点后在进行评估函数的倒推计算,这使得生成博弈树和估计值的倒推两个过程完全分离,因此搜索效率较低。
如果能边生成博弈树,边进行估值计算,则可能不必生成规定深度内的所有节点,以减少搜索的次数,这就是
α
−
β
\alpha-\beta
α−β过程。
好处: α − β \alpha-\beta α−β过程是吧生成后继节点和倒推评估函数的过程结合起来,及时减掉无用分支来提高算法效率,所以也称 α − β \alpha-\beta α−β剪枝
取MAX节点的最大下界为
α
\alpha
α值
而MIN节点的最小上界为
β
\beta
β值
步骤:
- 初始化 β \beta β为 + ∞ +\infty +∞, α \alpha α为 − ∞ -\infty −∞
- 从上至下MAX,MIN交替
- MAX层只改变 α \alpha α
- MIN层只改变 β \beta β
- α , β \alpha, \beta α,β是传递的
- 当 α > = β \alpha >= \beta α>=β时剪枝
下一篇
未完待续



![[仅供学习,禁止用于违法]编写一个程序来手动设置Windows的全局代理开或关,实现对所有网络请求拦截和数据包捕获(抓包或VPN的应用)](https://img-blog.csdnimg.cn/direct/c45234eb3fe64d999af6c6e2665999f1.png)