为了保留贝塞尔曲线的优点,同时克服贝塞尔曲线的缺点,b样条在贝塞尔曲线上发展而来,首先来看贝塞尔曲线的定义:

对于贝塞尔中的基函数而言,是确定的,全局唯一的,这导致了如果控制点发生变换将会对整个贝塞尔曲线产生影响。b样条采用了分段基函数(注意这里F的下标是i,k不同于贝塞尔中的i,n):

基函数的定义是分段的,是递归的:

原始控制点:

二阶b样条:

三阶b样条:

后续代码可能会放到GitHub。
参考文献:
《计算几何算法与实现》
1
2
3
b样条原理与测试
news2026/2/8 10:37:51
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1298091.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Linux基本指令(超详版)
Linux基本指令(超详版) 1. ls指令2.pwd指令3. cd 指令4.touch指令5mkdir指令6.rmdir指令&&rm指令7.man指令7.cp指令8.mv指令9.echo指令10.cat指令11.more指令12.less指令13.head指令14.tail指令15.date指令16.find指令17.grep指令zip(打包压缩) …
使用cmake构建Qt6.6的qt quick项目,添加应用程序图标的方法
最近,在学习qt的过程中,遇到了一个难题,不知道如何给应用程序添加图标,按照网上的方法也没有成功,后来终于自己摸索出了一个方法。 1、准备一张图片作为图标,保存到工程目录下面,如logo.ico。
…
二维码智慧门牌管理系统:引领未来的城市管理
文章目录 前言一、主要特点二、升级带来的优势与意义 前言
随着科技的快速发展,智能化管理已经成为我们生活和工作的重要方面。门牌管理系统是城市管理的基础设施之一,其智能化程度直接影响着城市管理的效率和质量。为了适应这一需求,二维码…
Helio 升级为 LISTA DAO,开启多链时代新篇章并宣布积分空投计划
Helio Protocol 是 BNB Chain 上排名第一的去中心化稳定币协议,其推出的超额抵押和清算机制支持的去中心化稳定币 HAY,在 BNB Chain 有非常广泛的应用,包括流动性挖掘、质押、交易、储值等! 2023 年 7 月,Helio Protoc…
【小沐学Python】Python实现语音识别(SpeechRecognition)
文章目录 1、简介2、安装和测试2.1 安装python2.2 安装SpeechRecognition2.3 安装pyaudio2.4 安装pocketsphinx(offline)2.5 安装Vosk (offline)2.6 安装Whisper(offline) 3 测试3.1 命令3.2 fastapi3.3 go…
C#注册表技术及操作
目录
一、注册表基础
1.Registry和RegistryKey类
(1)Registry类
(2)RegistryKey类
二、在C#中操作注册表
1.读取注册表中的信息
(1)OpenSubKey()方法
(2)GetSubKeyNames()…
SpringSecurity6 | 自定义认证规则
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: Java从入门到精通 ✨特色专栏…
Java基础-java.util.Scanner接收用户输入
目录 1. 导入所需要的jar包2. 编写代码运行3. 输出运行结果 1. 导入所需要的jar包
import java.util.Scanner;2. 编写代码运行
public class ScannerDemo {public static void main(String[] args) {/** 使用Scanner接收用户键盘输入的数据* 1. 导包:告诉程序去JD…
角谷定理 C语言xdoj32
角谷定理定义如下: 对于一个大于1的整数n,如果n是偶数,则n n / 2。如果n是奇数,则n 3 * n 1,反复操作后,n一定为1。 例如输入22的变化过程: 22 ->11 -> 34 -> 17 -> 52 -> 26 …
探索 Python 中链表的实现:从基础到高级
# 更多资料获取
📚 个人网站:ipengtao.com 链表是一种基础的数据结构,它由一系列节点组成,每个节点都包含数据和指向下一个节点的引用。在Python中,可以使用类来实现链表,本文将介绍如何实现链表ÿ…
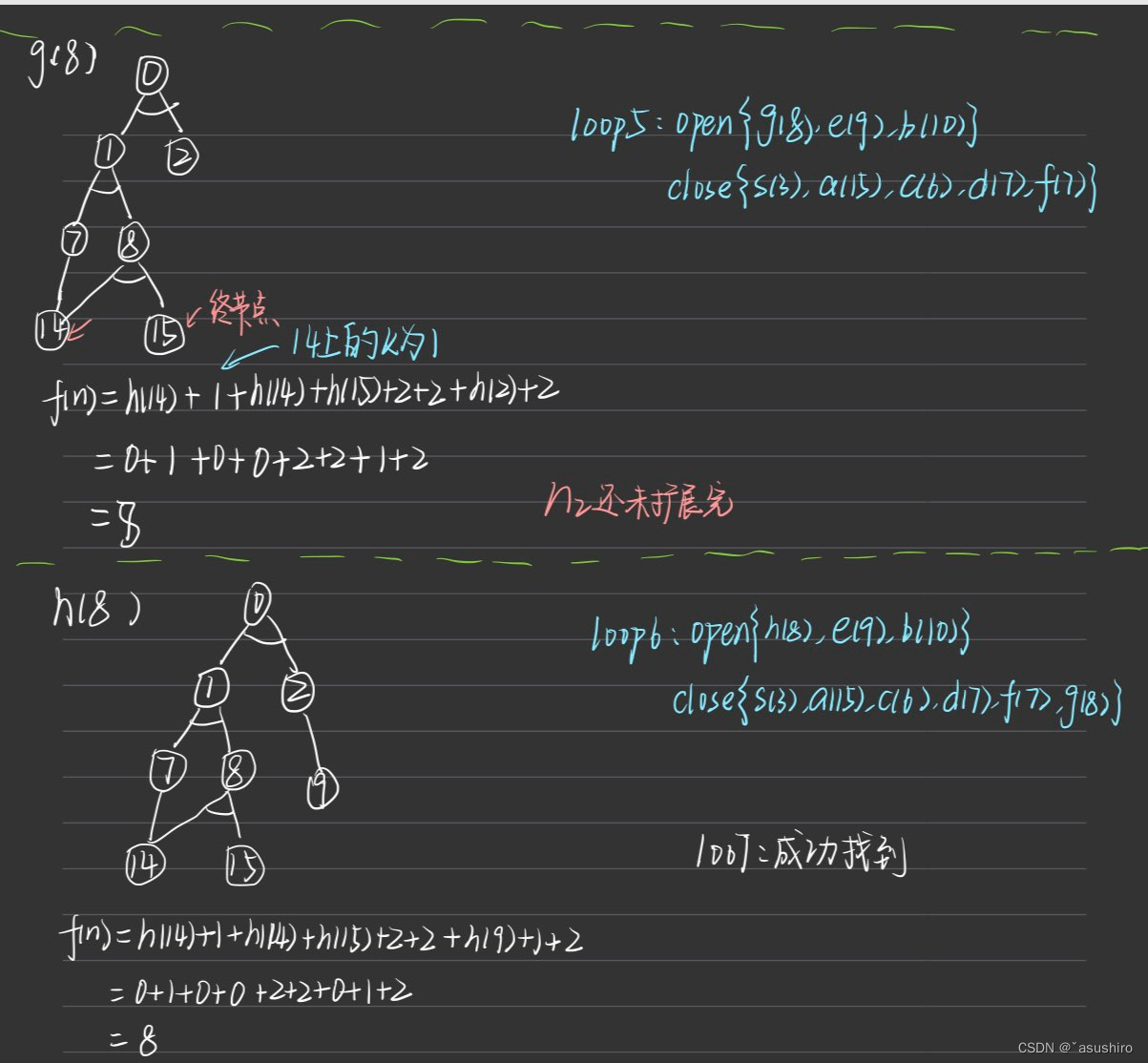
人工智能原理复习--搜索策略(二)
文章目录 上一篇启发式搜索与或图搜索博弈下一篇 上一篇
人工智能原理复习–搜索策略(一)
启发式搜索
提高一般图搜索效率的关键是优化OPEN表中节点的排序方式 最理想的情况是每次排序OPEN表表首n总在解答路径上
全局排序–对OPEN表中的所有节点进行…
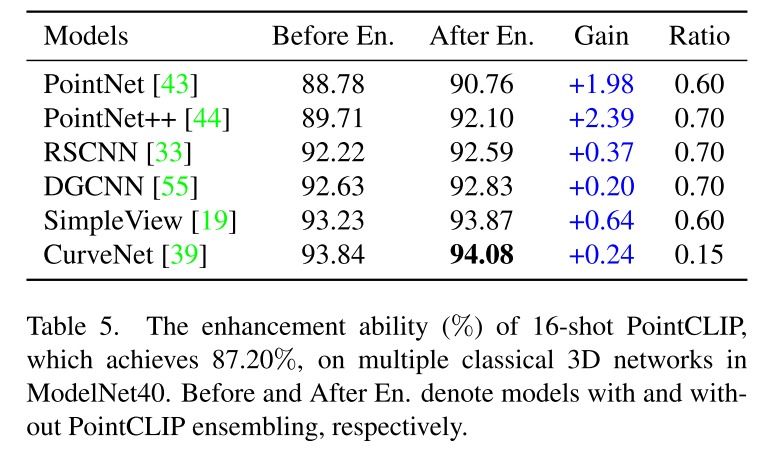
论文阅读:PointCLIP: Point Cloud Understanding by CLIP
CVPR2022
链接:https://arxiv.org/pdf/2112.02413.pdf
0、Abstract 最近,通过对比视觉语言预训练(CLIP)的零镜头学习和少镜头学习在2D视觉识别方面表现出了鼓舞人心的表现,即学习在开放词汇设置下将图像与相应的文本匹配。然而,…
内外联动——记建行江门鹤山支行营业部堵截一起新型骗局
建设银行广东省江门市分行(以下简称“江门建行”)认真贯彻落实党中央、国务院决策部署,紧紧围绕当地市委工作部署和上级行要求,扛牢国有大行责任,坚守金融工作的政治性、人民性,以深化新金融行动助力江门全…
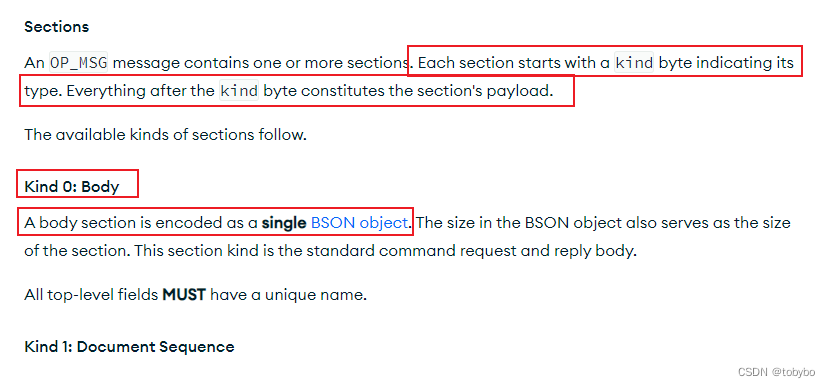
skynet 中 mongo 模块运作的底层原理解析
文章目录 前言总览全流程图涉及模块关系连接数据库函数调用流程图数据库操作函数调用流程图涉及到的代码文件 建立连接SCRAMSASL 操作数据库结语参考链接 前言
这篇文章总结 skynet 中 mongo 的接入流程,代码解析,读完它相信你对 skynet 中的 mongo 调用…
Python数据科学视频讲解:数据清洗、特征工程和数据可视化的注意事项
1.6 数据清洗、特征工程和数据可视化的注意事项 视频为《Python数据科学应用从入门到精通》张甜 杨维忠 清华大学出版社一书的随书赠送视频讲解1.6节内容。本书已正式出版上市,当当、京东、淘宝等平台热销中,搜索书名即可。内容涵盖数据科学应用的全流程…
【数电笔记】58-同步D触发器
目录
说明:
1. 电路组成
2. 逻辑功能
3. 特性表、特性方程
4. 状态转移图
例题
5. 同步D触发器的特点
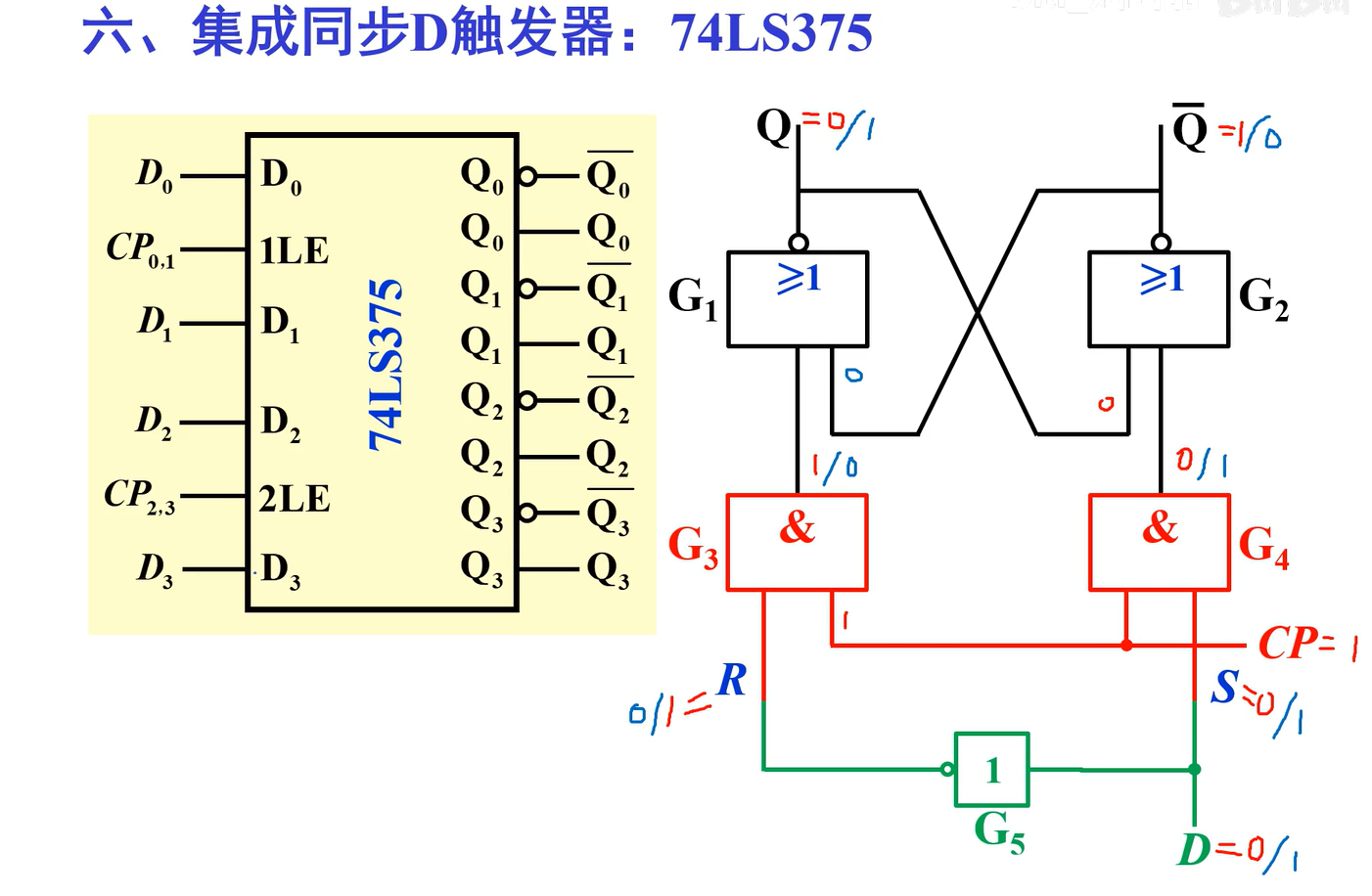
6. 集成同步D触发器:74LS375
74LS375内部原理 说明:
笔记配套视频来源:B站本系列笔记并未记录所有章节,…
2024最新软件测试面试最全八股文
请你说一说测试用例的边界
参考回答:
边界值分析法就是对输入或输出的边界值进行测试的一种黑盒测试方法。通常边界值分析法是作为对等价类划分法的补充,这种情况下,其测试用例来自等价类的边界。
常见的边界值
1)对16-bit 的整数而言 32…
[仅供学习,禁止用于违法]编写一个程序来手动设置Windows的全局代理开或关,实现对所有网络请求拦截和数据包捕获(抓包或VPN的应用)
文章目录 介绍一、实现原理二、通过注册表设置代理2.1 开启代理2.2 关闭代理2.3 添加代理地址2.4 删除代理设置信息 三、代码实战3.1 程序控制代理操作控制3.1.1 开启全局代理3.1.2 添加代理地址3.1.3 关闭代理开关3.1.4 删除代理信息 3.2 拦截所有请求 介绍 有一天突发奇想&am…










![[仅供学习,禁止用于违法]编写一个程序来手动设置Windows的全局代理开或关,实现对所有网络请求拦截和数据包捕获(抓包或VPN的应用)](https://img-blog.csdnimg.cn/direct/c45234eb3fe64d999af6c6e2665999f1.png)