【C递归】
- 前言
- 一、兔子繁殖问题
- (一)题目描述
- (二)解题
- 1.递归做法
- (1)成兔
- (i)分析
- (ii)代码
- (iii)代码分析
- (2)幼兔
- (i)分析
- (ii)代码
- (iii)代码分析
- (3)总的兔子个数
- (i)分析
- (ii)代码
- (iii)分析
- (iv)代码
- 2.迭代做法
- (1)成兔
- (i)分析
- (ii)代码
- (2)幼兔
- (i)分析
- (ii)代码
- (3)总数
- (i)分析
- (ii)代码
- 二、青蛙跳台阶问题
- (一)前言
- (二)题目描述
- (三)解题
- 1.递归做法
- (1)分析
- (2)代码
- (3)代码分析
- 2.迭代做法
- (1)分析
- (2)代码
- (3)代码分析
- 三、汉诺塔问题
- (一)题目概述
- (二)思路及解题步骤
- (三)代码
- (四)解题思路
- 总结
前言
汉诺塔问题和青蛙跳台阶问题是C语言函数递归中很重要的两个问题,我们既可以用递归的方式进行编译,也可以用迭代的方法进行编译。一提到递归大家可能会觉得好难,可是真有那么难吗,以下两道经典的递归题目让大家完全了解递归。
一、兔子繁殖问题
(一)题目描述
在解决下面两个问题之前,我们先来看一个比较经典的问题,就是兔子繁殖问题,即我们常说的斐波那契数列,这个问题是怎么编译的呢?我们可以先查一查兔子是如何繁殖的?
题目描述:一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
题目说的是在两个月后才能繁殖,我们拿一对幼兔做实验,前两个月是只有一对成年兔子的,如下图:

(二)解题
1.递归做法
(1)成兔
(i)分析
先看成年兔子:
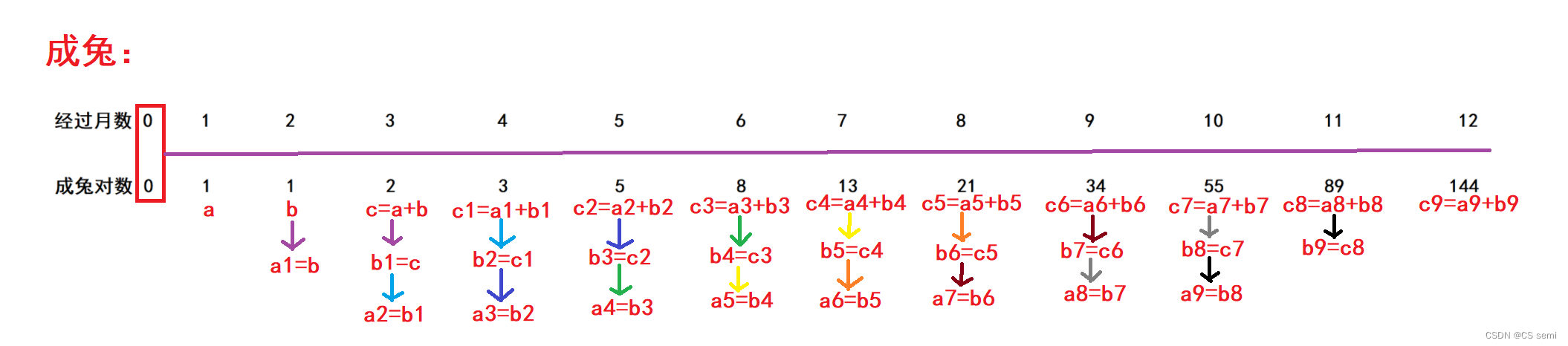
我们列出来了12个月,一年成年兔子的总对数,我们发现其排列的是0 1 1 2 3 5 8 13 21 34 55 89 144,这似乎看不出什么规律来,那我们画个图吧!

大家要仔细想想,这怎么后一个月的成兔等于前两个月的成兔之和。我们拿前四个月的兔子进行比较,如图:
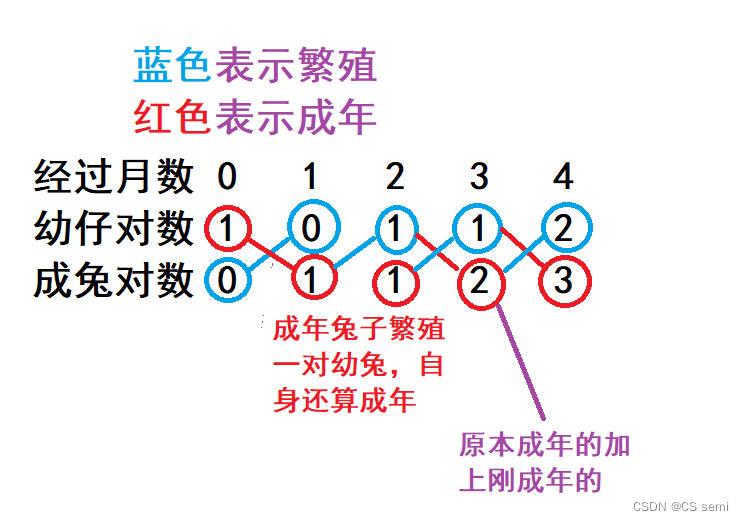
成兔的个数是原本已经成年的加一下上上次所繁殖的幼兔此时成年的新成兔,由于一对成兔只能生一对,那也就是上上次的成兔加上上次的成兔,如下图,给出公式:
那我们就用递归函数来写一下吧!!!
(ii)代码
#include<stdio.h>
int fib(int n) {
if (n == 0) {
return 0;
}
else if ((n == 1) || (n == 2)) {
return 1;
}
else { //n>2
return fib(n - 1) + fib(n - 2);
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d\n", ret);
return 0;
}
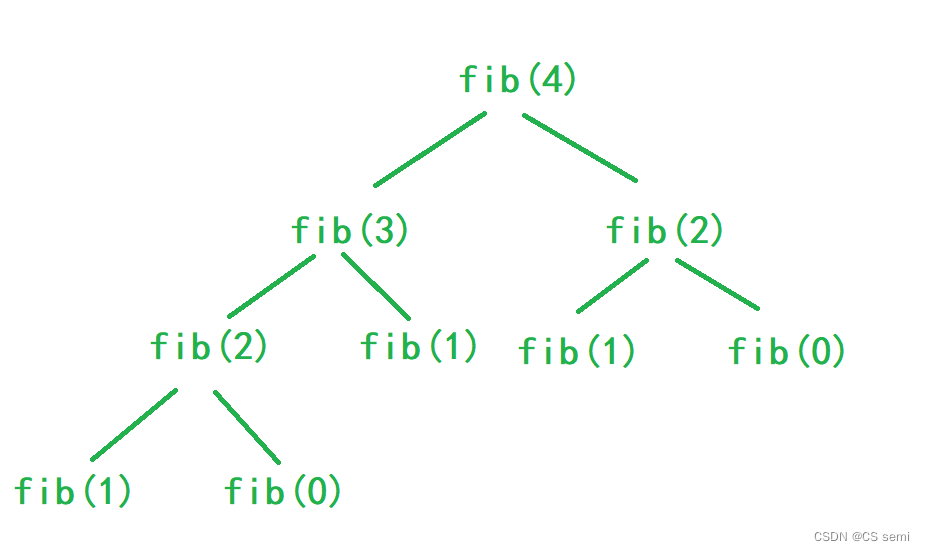
(iii)代码分析
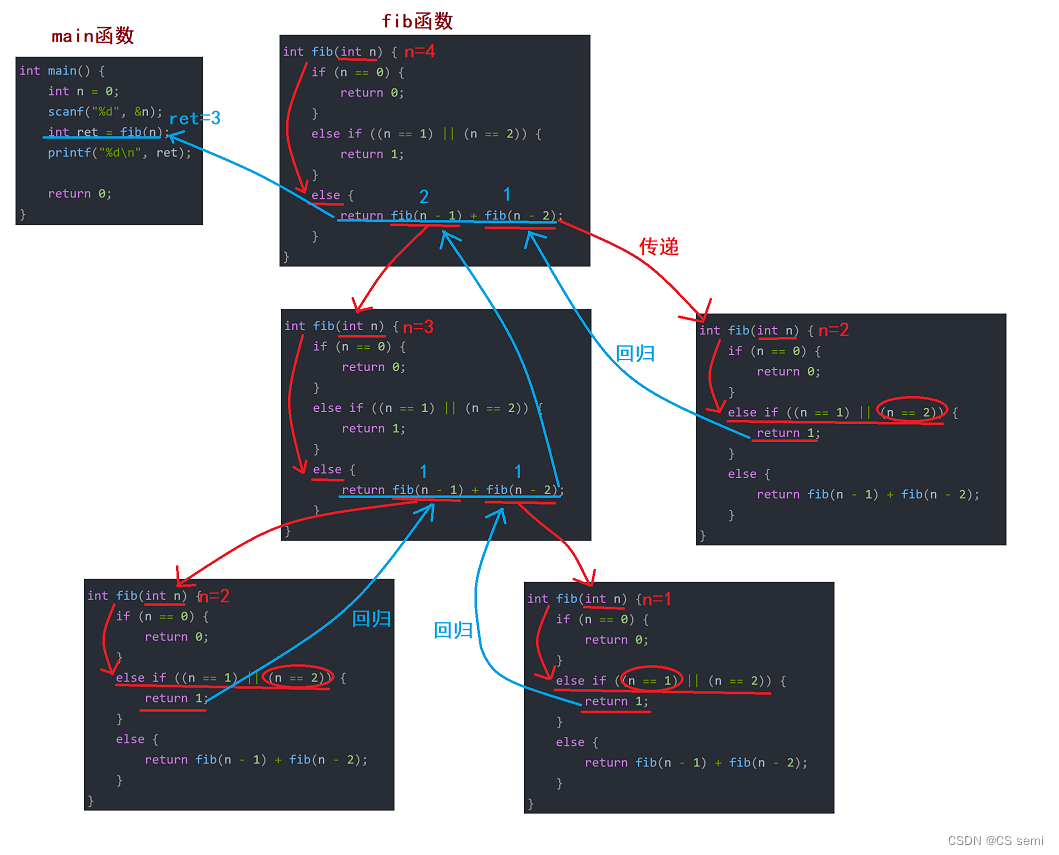
如上图进行递归。
(2)幼兔
(i)分析
大家可能觉得幼兔很难算,可是大家一想,幼兔是之前成兔繁殖的新幼兔,而成兔是怎么来的,成兔是本已经成年的加一下上上次所繁殖的幼兔此时成年的新成兔,也就是上上次的成兔加上上次的成兔,那幼兔可想而知那不就是上一个月的成兔个数嘛!!!这不就是一个递归嘛,还是上上个月的幼兔加上上个月幼兔。是不是很奇妙,那我们开始写代码吧!
(ii)代码
#include<stdio.h>
int fib1(int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 0;
}
else if (n == 2) {
return 1;
}
else { //n>2
return fib1(n - 1) + fib1(n - 2);
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret1 = fib1(n);
printf("%d\n", ret1);
return 0;
}
(iii)代码分析
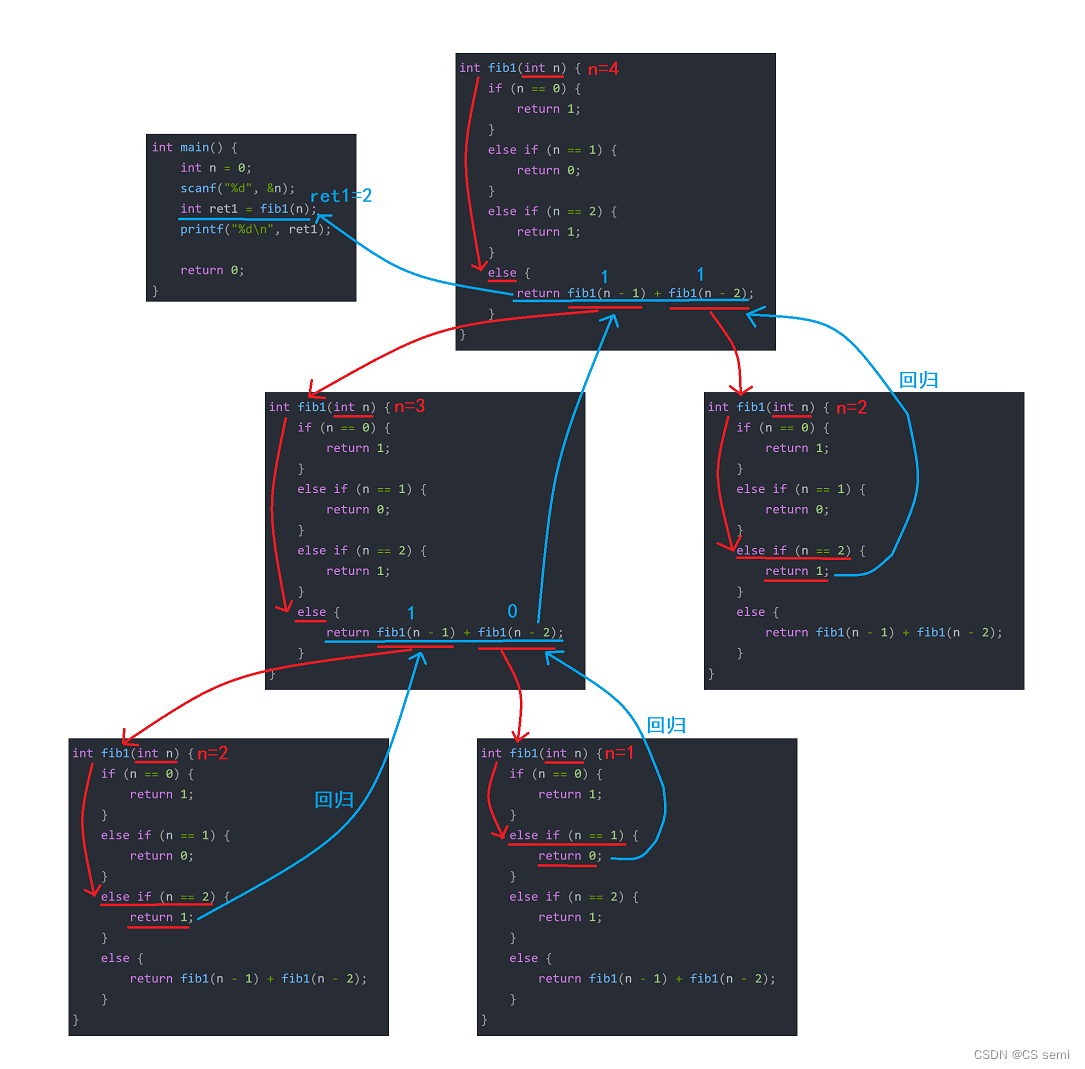
(3)总的兔子个数
(i)分析
既然是总的兔子个数,那就很简单了,是本月的幼兔加上成兔,那不就是那两串代码合起来吗?那我们来试一试吧!
(ii)代码
#include<stdio.h>
//成兔
int fib(int n) {
if (n == 0) {
return 0;
}
else if ((n == 1) || (n == 2)) {
return 1;
}
else { //n>2
return fib(n - 1) + fib(n - 2);
}
}
//幼兔
int fib1(int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 0;
}
else if (n == 2) {
return 1;
}
else { n>2
return fib1(n - 1) + fib1(n - 2);
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = fib(n);
int ret1 = fib1(n);
printf("成兔=%d\n", ret);
printf("幼兔=%d\n", ret1);
int ret2 = ret + ret1;
printf("总数=%d\n", ret2);
return 0;
}
运行代码截图:
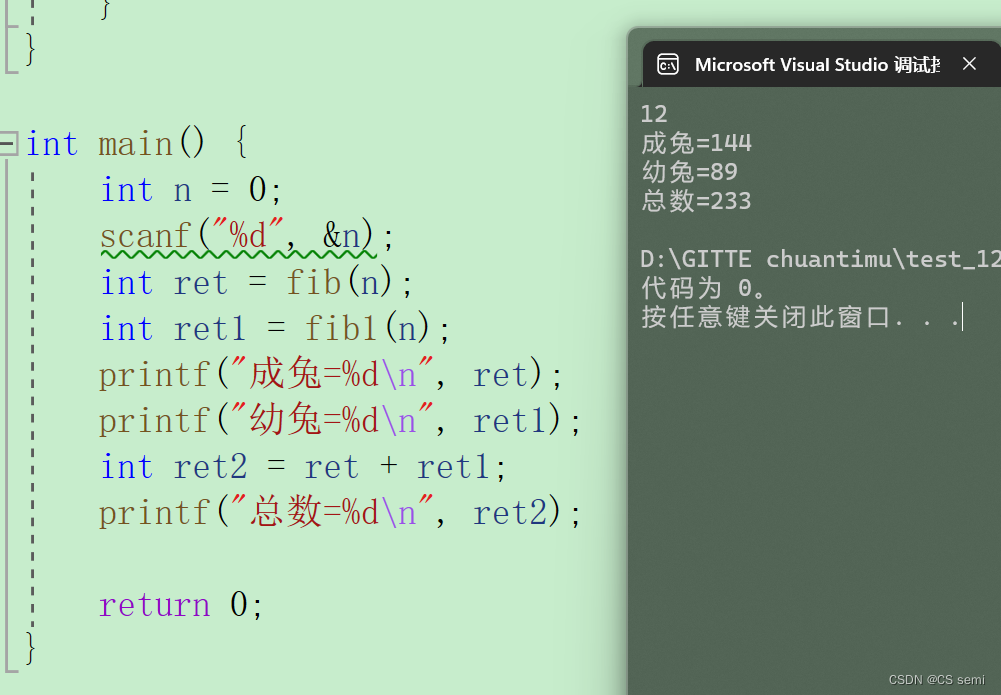
(iii)分析
此外,大家发现了吗?这个总数居然也是个斐波那契数列,大家可以仔细想想,本月的总的兔子数是上个月成兔生的同等数列的幼兔加上上个月的成兔再加一下上上个月生的同样数量的幼兔本月成年,那不就是上个两份的上个月成兔加上上个月的幼兔,我们发现,本月的兔子总数岂不是下个月的成兔数量吗,为什么呢?因为下个月的成兔是本月成兔的数量加上本月幼兔在下个月成熟的数量,哦~原来如此,这总数岂不是就是成兔的斐波那契数列往前推一位吗?那不也是一个斐波那契吗?
那我们试试写代码吧!
(iv)代码
#include<stdio.h>
//成兔
int fib(int n) {
if (n == 0) {
return 0;
}
else if ((n == 1) || (n == 2)) {
return 1;
}
else { //n>2
return fib(n - 1) + fib(n - 2);
}
}
//幼兔
int fib1(int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 0;
}
else if (n == 2) {
return 1;
}
else { //n>2
return fib1(n - 1) + fib1(n - 2);
}
}
//总数
int fib2(int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 1;
}
else {
return fib2(n - 1) + fib2(n - 2);
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = fib(n);
int ret1 = fib1(n);
printf("成兔=%d\n", ret);
printf("幼兔=%d\n", ret1);
int ret2 = fib2(n);
printf("总数=%d\n", ret2);
return 0;
}
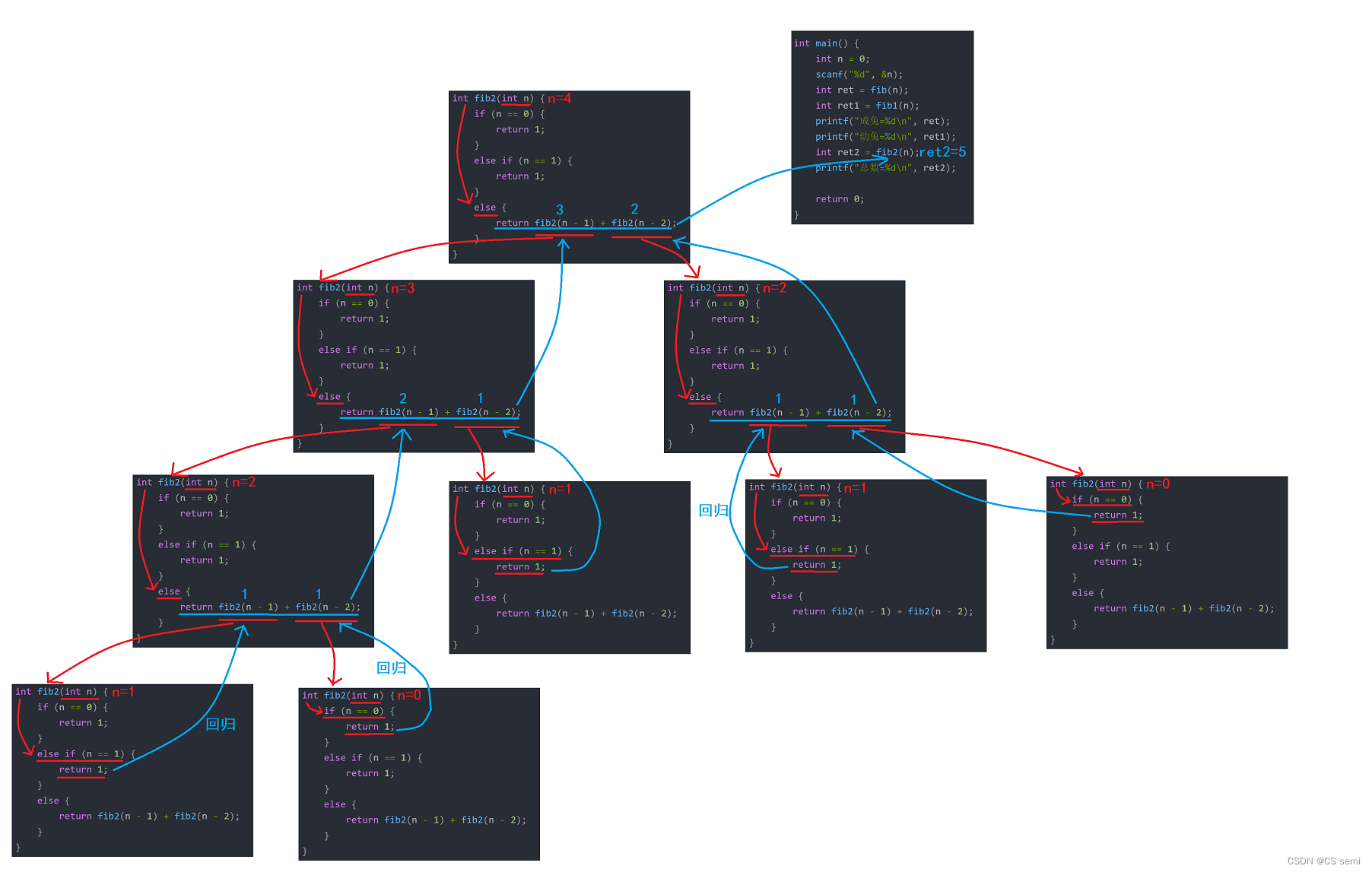
2.迭代做法
(1)成兔
(i)分析
思路具体和递归做法一样,但不同的点是做法,我们思考一下,a,b为第一个月和第二个月的成兔数量,第三个月成兔数量c=a+b,我们继续往下看,第四个月成兔数量为d=b+c=b+a+b,第五个月成兔数量为e=c+d=c+b+c=a+b+b+a+b,大家有发现什么奇特的地方吗,如果我们把c的值赋给b,把b的值赋给a,用已经算得的结果赋给前面的值再进行相加求出后面的结果。如下图:
(ii)代码
#include<stdio.h>
//成兔对数
int fib(int n) {
if (n == 0) {
return 0;
}
else if (n == 1 || n == 2) {
return 1;
}
else {//n>2
int a = 1;//第一个月
int b = 1;//第二个月
int c = 0;//第三个月
//a,b分别为前两项,c为前两项的和,得到c的值后更新a,b的值
while (n > 2) {//更新a,b
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("成兔=%d\n", ret);
return 0;
}
(2)幼兔
(i)分析
幼兔的思路和成兔的思路一样的,我们既可以用第0个月来作为a,也可以用第1个月来作为a进行计算。
(ii)代码
#include<stdio.h>
//幼兔对数
int fib1(int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 0;
}
else if (n == 2) {
return 1;
}
else {//n>2
int a = 0;//第一个月
int b = 1;//第二个月
int c = 0;//第三个月
//a,b为前两项,c为前两项的和,得到的c用以更新a,b的值
while (n > 2) {//更新a,b的值
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret1 = fib1(n);
printf("幼兔=%d\n", ret1);
return 0;
}
(3)总数
(i)分析
总数这里就有两种做法,一种是幼兔加成兔;另一种是再利用迭代的思想,只不过这次前面的a,b的值要发生变化。
(ii)代码
//相加
#include<stdio.h>
//成兔对数
int fib(int n) {
if (n == 0) {
return 0;
}
else if (n == 1 || n == 2) {
return 1;
}
else {//n>2
int a = 1;//第一个月
int b = 1;//第二个月
int c = 0;//第三个月
//a,b分别为前两项,c为前两项的和,得到c的值后更新a,b的值
while (n > 2) {//更新a,b
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}
//幼兔对数
int fib1(int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 0;
}
else if (n == 2) {
return 1;
}
else {//n>2
int a = 0;//第一个月
int b = 1;//第二个月
int c = 0;//第三个月
//a,b为前两项,c为前两项的和,得到的c用以更新a,b的值
while (n > 2) {//更新a,b的值
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("成兔=%d\n", ret);
int ret1 = fib1(n);
printf("幼兔=%d\n", ret1);
int ret2 = ret + ret1;
printf("总数=%d\n", ret2);
return 0;
}
//迭代思想
#include<stdio.h>
//成兔对数
int fib(int n) {
if (n == 0) {
return 0;
}
else if (n == 1 || n == 2) {
return 1;
}
else {//n>2
int a = 1;//第一个月
int b = 1;//第二个月
int c = 0;//第三个月
//a,b分别为前两项,c为前两项的和,得到c的值后更新a,b的值
while (n > 2) {//更新a,b
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}
//幼兔对数
int fib1(int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 0;
}
else if (n == 2) {
return 1;
}
else {//n>2
int a = 0;//第一个月
int b = 1;//第二个月
int c = 0;//第三个月
//a,b为前两项,c为前两项的和,得到的c用以更新a,b的值
while (n > 2) {//更新a,b的值
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}
//总数
int fib2(int n) {
if (n == 0) {
return 1;
}
else if (n == 1) {
return 1;
}
else {
int a = 1;//第0个月
int b = 1;//第1个月
//a,b为前两项,c为前两项的和,得到的c用以更新a,b的值
int c = 0;//第2个月
while (n > 1) {//更新a,b的值
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("成兔=%d\n", ret);
int ret1 = fib1(n);
printf("幼兔=%d\n", ret1);
int ret2 = fib2(n);
printf("总数=%d\n", ret2);
return 0;
}
解决了兔子繁殖的问题,那我们继续看一下青蛙跳台阶的问题!
二、青蛙跳台阶问题
(一)前言
在解决这个问题之前,我想吐槽一下在大一上学期进入实验室的纳新题,大家看一下下面的图:

出题目的人是比较喜欢玩LOL的自由天使呀!让人抓不住头脑,在网上搜了半天没查出来,到今天我再看一看这个题目的时候,也是被自己之前笑到了,这些题目果然只需要把知识点揪出来就可以做了,不用理会主人公什么操作什么的,那接下来我们看一看吧!
(二)题目描述
有一只青蛙,它碰到一个楼梯挡了它的路,它需要越过这个楼梯,可是受于楼梯高度,它一次只能选择跳一个台阶或者两个台阶,那它跳过这段台阶有多少次方式呢?
(三)解题
这个题目看起来很难,如果用穷举法,一个台阶一个跳法,两个台阶两种跳法,三个台阶三种跳法,四个台阶五个跳法,五个台阶8个跳法……我的天哪,这不是越来越多了吗,穷举法找不出通项来啊!那我们重新想一想,画个图试一试:
1.递归做法
(1)分析
先来一张图片看一看:
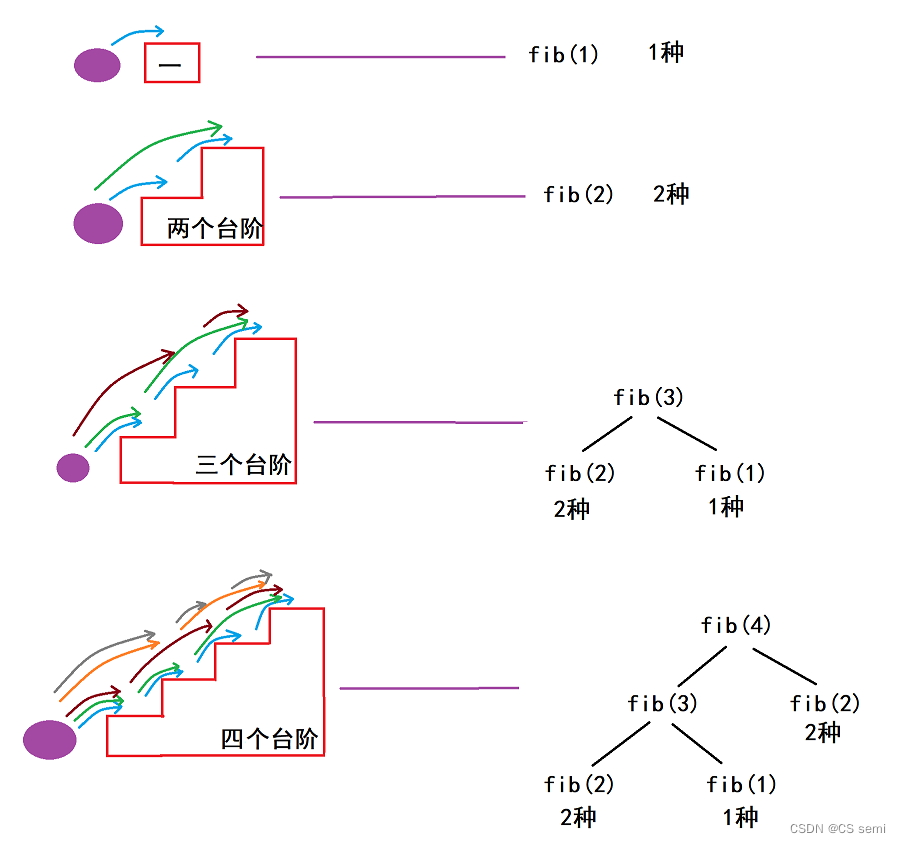
我们看:
1个台阶:只需要跳一个台阶。
2个台阶:选择一个一个跳和一次跳两个。
3个台阶:1、先跳一个台阶,分出两条路一个一个跳,直接跳两个台阶2.先跳两个,再跳一个台阶。 即:先跳了一个,则还剩两个,就是跳两个的情况;先跳了两个,则还剩一个,就是跳一个台阶的情况。 所以跳三个=跳一个+跳两个
4个台阶:1.先跳一个台阶,再分出三条路,一个一个跳,先跳一个再跳两个,先跳两个再跳一个。2.先跳两个,分出两条路,一个一个跳,直接跳两个。 即:先跳了一个,则还剩三个,就是跳三个的情况;先跳了两个,则还剩两个,就是跳两个的情况。 所以跳四个=跳两个+跳三个。
……
大家有没有看到,这不就是斐波那契数列嘛,青蛙肯定是先选择跳一个和两个的情况,后面的情况根据递归能进行解决,就是前两次之和。那我们来写一下代码吧!
(2)代码
#include<stdio.h>
int fib(int n) {
if (n == 1) {
return 1;
}
else if (n == 2) {
return 2;
}
else {
return fib(n - 1) + fib(n - 2);
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d\n", ret);
return 0;
}
至于为何是把1和2单拎出来,原因是大家可以想青蛙跳一次无非是使剩余台阶-1或者-2,且可以知道最终都会回到剩余1个或两个台阶的情况,因此我们是可以根据这两个情况即fib(1)=1和fib(2)=2以基准来进行递归的。
(3)代码分析
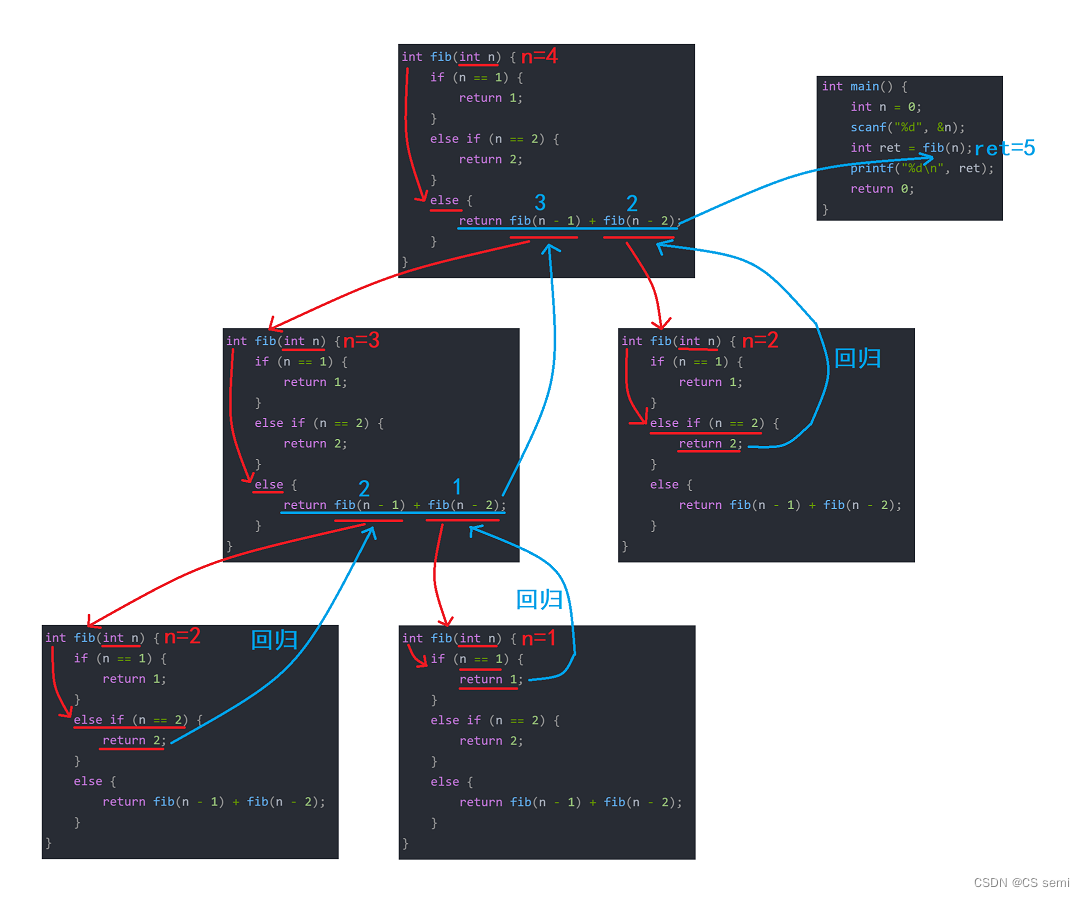
2.迭代做法
(1)分析
迭代做法和前面的一样,只要前面的看懂了,这里的问题就会迎刃而解。
(2)代码
#include<stdio.h>
int fib(int n) {
if (n == 1) {
return 1;
}
else if (n == 2) {
return 2;
}
else {
int a = 1;//跳一个台阶
int b = 2;//跳两个台阶
int c = 0;
//c为前两项之和,更新a,b的值以达到迭代目的
while (n > 2) {//更新a,b的值
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("青蛙总共有%d种跳法\n", ret);
return 0;
}
(3)代码分析

三、汉诺塔问题
(一)题目概述
相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
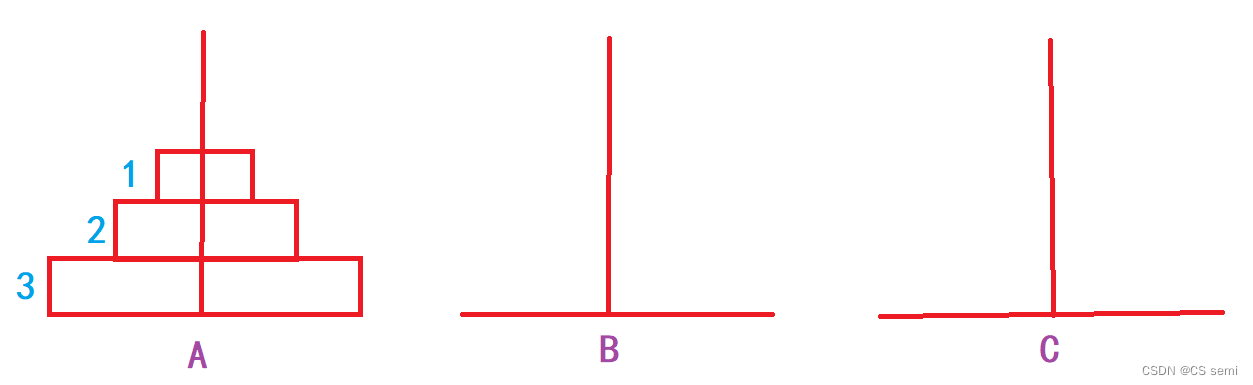
(二)思路及解题步骤
一个盘子:移动一个盘子到C柱子。
两个盘子:1->B,2->C,1->C。
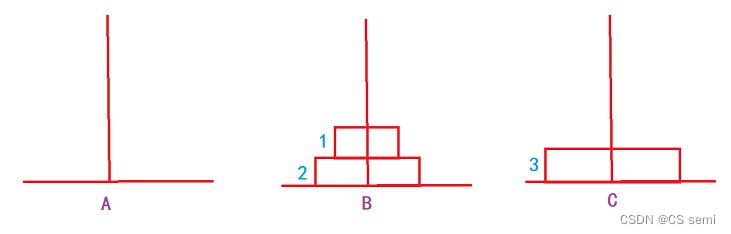
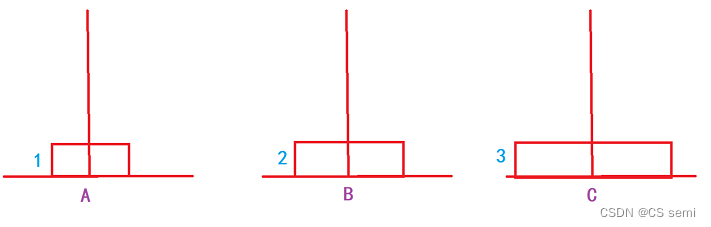
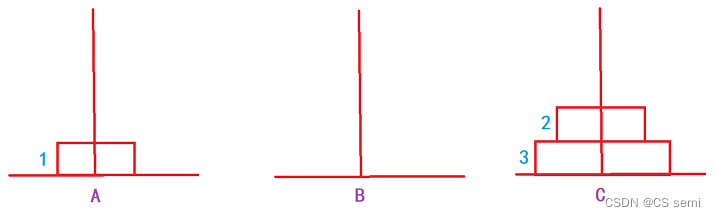
三个盘子:1->C,2->B,1->B,3->C,1->A,2->C,3->C。
四个盘子:1->B,2->C,1->C,3->B,1->A,2->B,1->B,4->C,1->C,2->A,1->A,3->C,1->B,2->C,1->C。
……
在这个操作过程当中,大家有没有发现一个很有趣的现象,当盘子是三个的时候,是先在三个柱子分布的是1,2,0的圆盘个数,也就是说,先排好了两个,再去排底下那个最大的圆盘。在排四个圆盘的时候,我们发现排到第一步的时候是先排到三根柱子的数量为:2,2,0。再继续排,排到第二步的时候发现三根柱子的个数为:1,3,0。不知道大家发现了没有,当我们排的时候,是先要排完n-1个圆盘再去排最后一个,而n-1个圆盘是怎么排的呢?那就是先排好n-2个圆盘再去排第n-1个圆盘。是不是很神奇,那我们
以三个圆盘为例:
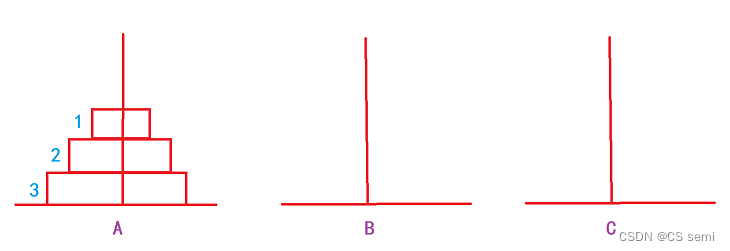
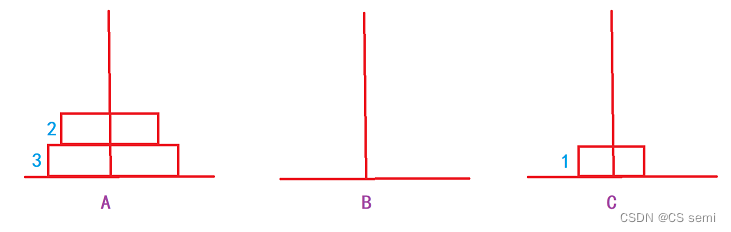
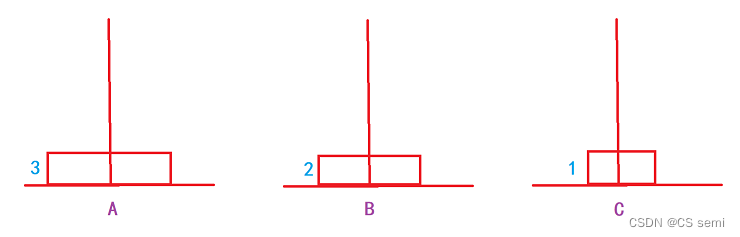
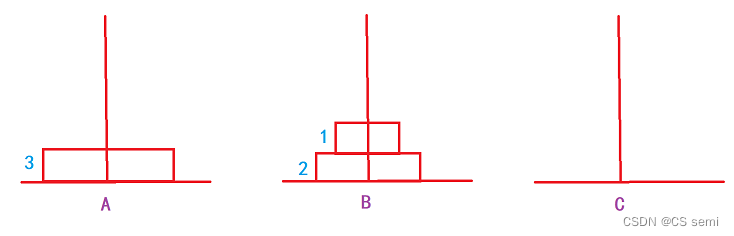

(三)代码
#include<stdio.h>
//思路:先借助C柱子移动到B柱子,
//再把A柱子最后一个大圆盘移动到C柱子上,
//最后再借助A柱子将B柱子内的圆盘移动到C柱子上
//Hanoi(从哪根柱子,借助哪根柱子,移动到哪根柱子,盘子数量)
int i = 0;//使用一个全局变量统计次数
void move(char x, char y, int n){
printf("把第%d个圆盘从%c柱->%c柱\n", n, x, y);
i++;
}
void Hanoi(char A, char B, char C, int n){
if (n == 1){
//调用1次move
move(A, C, n);
}
else{
//先将n-1个圆盘从A柱借助C柱移动到B柱上
Hanoi(A, C, B, n - 1);
//再将A柱子最后一个圆盘移动到C柱上
move(A, C, n);
//最后将n-1个圆盘从B柱借助A柱移动到C柱上
Hanoi(B, A, C, n - 1);
}
}
int main(){
int n = 0;
printf("请输入首先在A柱子上的圆盘个数:>");
scanf("%d", &n);
//将n个圆盘从A柱借助于B柱移动到C柱上
Hanoi('A', 'B', 'C', n);
printf("次数总共为:%d次\n", i);
return 0;
}
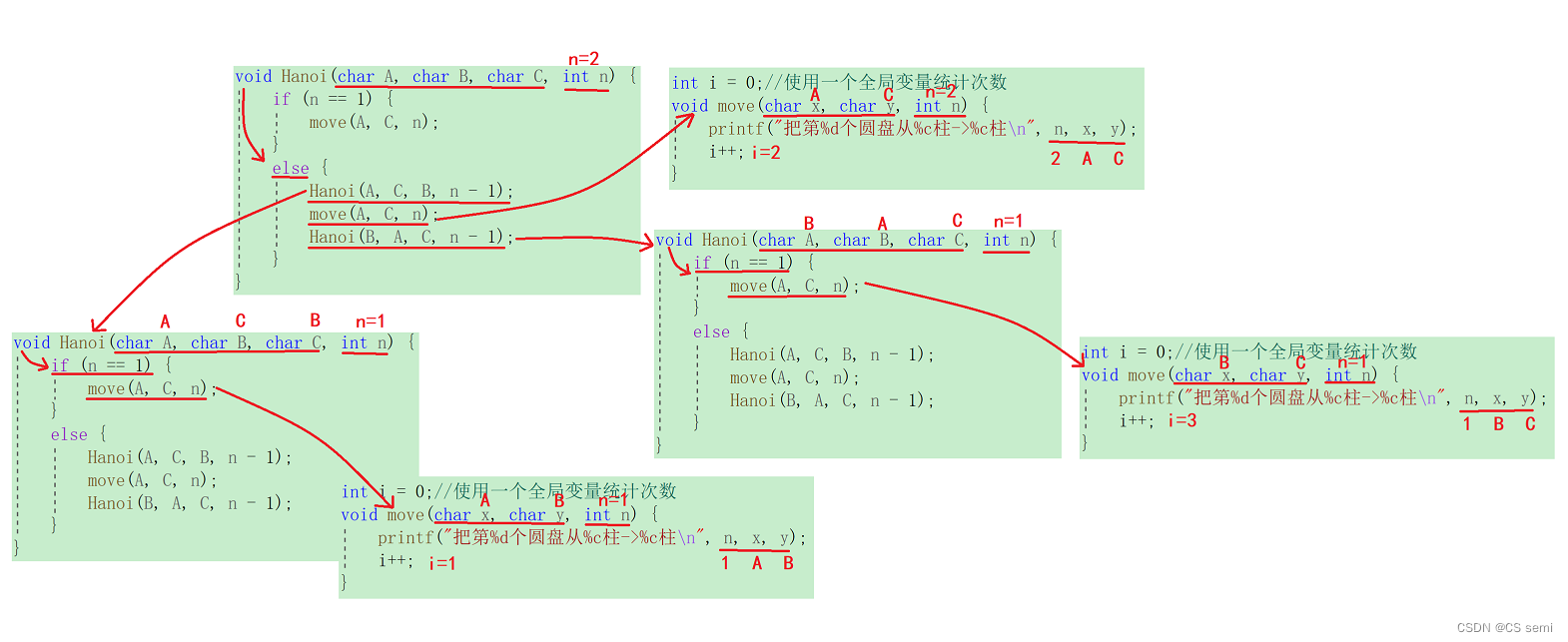
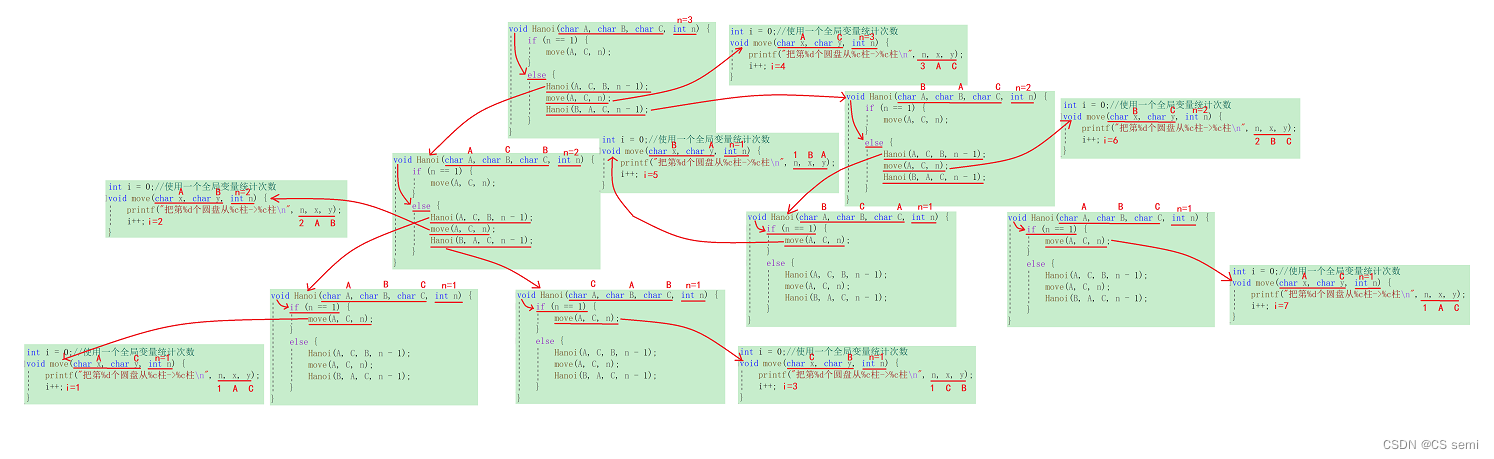
(四)解题思路
这个递归解题有点复杂,先来个n=2的预热一下,再来个n=3的深层理解一下。
总结
递归的逻辑是很复杂的,是有缺陷的,但递归是一个很好的解题思路,可以锻炼自己的代码能力,我们今天学习到了这三个问题,相信大家肯定能很好的掌握递归与迭代的问题!!!
客官,码字不易,给个三连支持一下吧!!!