Every day a Leetcode

题目来源：2477. 到达首都的最少油耗

解法1：贪心 + 深度优先搜索

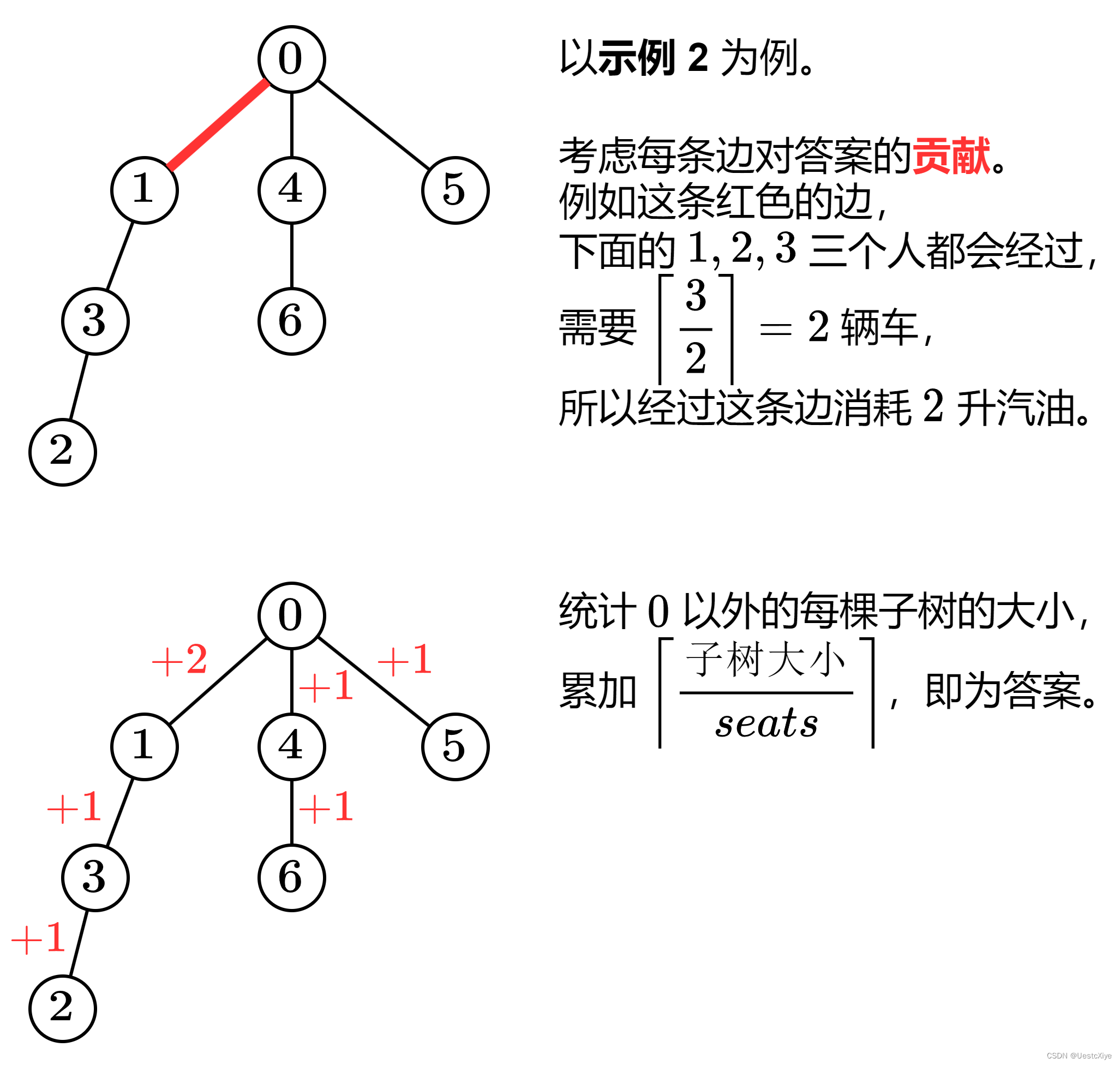
题目等价于给出了一棵以节点 0 为根结点的树，并且初始树上的每一个节点上都有一个人，现在所有人都需要通过「车子」向结点 0 移动。

对于某一个节点 x（x 不等于 0），其父节点为 y，因为以节点 x 为根节点的子树上的人都需要通过边 x->y 向节点 0 移动，所以为了使这条边上的「车子」利用率最高，我们贪心的让 x 的全部子节点上的人到了节点 x 再一起坐车向上移动，我们不妨设以节点 x 为根节点的子树大小为 cnt_x，那么我们至少需要「车子」的数量为⌈cnt_x/seats⌉，其中 seats 是每辆车里面座位的数目。

那么我们可以通过从根结点 0 往下进行「深度优先搜索」，每一条边上「车子」的数目即为该条边上汽油的开销，统计全部边上汽油的开销即为最终答案。

示例：

代码：

/*
 * @lc app=leetcode.cn id=2477 lang=cpp
 *
 * [2477] 到达首都的最少油耗
 */

// @lc code=start
class Solution
{
private:
    long long ans = 0;

public:
    long long minimumFuelCost(vector<vector<int>> &roads, int seats)
    {
        // 特判
        if (roads.empty() || seats == 0)
            return 0;
        int n = roads.size();
        vector<vector<int>> edges(n + 1);
        for (vector<int> &road : roads)
        {
            int from = road[0], to = road[1];
            // 记录每个点的邻居
            edges[from].push_back(to);
            edges[to].push_back(from);
        }
        function<int(int, int)> dfs = [&](int x, int father) -> int
        {
            int subTreeSize = 1;
            for (int &y : edges[x])
                if (y != father) // 递归子节点，不能递归父节点
                {
                    // 统计子树大小
                    subTreeSize += dfs(y, x);
                }
            if (x != 0) // x 不是根节点
                ans += ceil(1.0 * subTreeSize / seats);
            return subTreeSize;
        };
        dfs(0, -1);
        return ans;
    }
};
// @lc code=end

结果：

复杂度分析：

时间复杂度：O(n)，其中 n 是数组 roads 的长度。递归这棵树，每个节点至多访问一次。

空间复杂度：O(n)，其中 n 是数组 roads 的长度。