该内容为重拾部分线性代数知识的学习笔记,内容上更多的是为了解决问题而学习的内容,并非系统化的学习。
针对的问题为:Music算法推导求解过程中的矩阵计算知识。
学习的内容包括:矩阵原理、矩阵行列式、矩阵的秩、线性变换矩阵变换、单位矩阵与逆矩阵、特征值和特征向量。
推荐学习视频:bilibili的视频:【线性代数全集从入门到精通(清楚易懂,看过的都说好,哈哈)】 https://www.bilibili.com/video/BV1wL411H7x1/?share_source=copy_web&vd_source=a0df23ab5f45bf4a580c20684f4a6705
一. 矩阵
-
线性方程组
线性方程组,多元x1 x2 x3等组成的线性方程组。线性方程组的解只有三种情况:0个解、1个(组)解和无穷多个解。
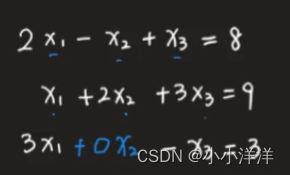
-
增广矩阵
增广矩阵为系数矩阵+常数项矩阵,是一种更简单的表达。

-
理想矩阵:阶梯型矩阵、对角矩阵
通过对矩阵进行初等行变换,即行的倍数、行的叠加、行的倍数再叠加,矩阵的解不变。
从最下面一行开始消元,得到理想型矩阵可以方便求解元,该方法叫做高斯消元法。
阶梯型矩阵就可以方便求解,对角矩阵则是更加理想的矩阵。
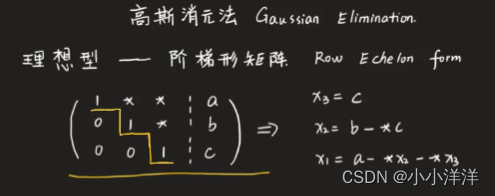
-
矩阵与向量
空间中的向量,可以用多个正交单位向量的组合表示。
多个向量的线性组合为这些向量的向量空间。
线性相关:多个向量的线性组合能够等于0,其中他们的系数不全为0,即线性相关,否则线性无关。
定义:n+1个n维向量一定是线性相关的。因为n个不相关的向量已经组成了整个n维的自由空间,多一个肯定是在这个自由空间中的。
向量的计算:数乘、加法、线性组合。

-
齐次方程组
齐次方程组的常数矩阵为0,即Ax = 0

-
矩阵乘法
矩阵乘法中,左边矩阵的列数要等于右边矩阵的行数。
二、矩阵行列式
- 行列式可以Det(A)表示
- 行列式为符号系数+子矩阵行列式的叠加。
三、矩阵秩
- 秩的定义
矩阵的秩为最高阶非零子式的阶数。

- 秩对求解个数的意义
系数矩阵的秩=增广矩阵的秩:1个解
系数矩阵的秩<增广矩阵的秩:0个解
系数矩阵的秩>增广矩阵的秩:无穷个解
四、线性变换、矩阵变换
- 线性变换和矩阵变换
这两种变换是可以在一定程度上转换的。
五、单位矩阵与逆矩阵
- 单位矩阵

- 逆矩阵
逆矩阵与原矩阵的乘积为单位矩阵。
逆矩阵的计算可以由下述公式计算,分母为矩阵行列式,也可以用Det(A)表示,选取最佳的一行(0比较多的行)进行计算。分子为伴随矩阵。


六、特征值与特征向量
-
特征值和特征向量
矩阵和特征向量的乘积,正好为一个特征值与该特征向量的乘积。即矩阵的乘积,只改变该方向的大小,而不改变方向。
特征向量表达了方向,特征值表达了大小。
个人理解:特征向量意味着该矩阵在这个方向上的映射。

-
特征值计算
Ax = λx
Ax = λIx
(A-λI)x = 0
Det(A-λI) = 0
得到多个特征值 -
特征向量的计算
带入特征值到上式,进行计算和求解。

-
意义
几何意义为变换效果只发生缩放,不发生其他如旋转、平移。
代数意义为矩阵的内部结构进行了分解和化解。
七、协方差矩阵
- 协方差矩阵
个人理解:表达了两个矩阵之间的关联性。


![[笔记]ARMv7/ARMv8 交叉编译器下载](https://img-blog.csdnimg.cn/direct/8be7ad0ab8b740a8b5a2ab30b90233e1.png)