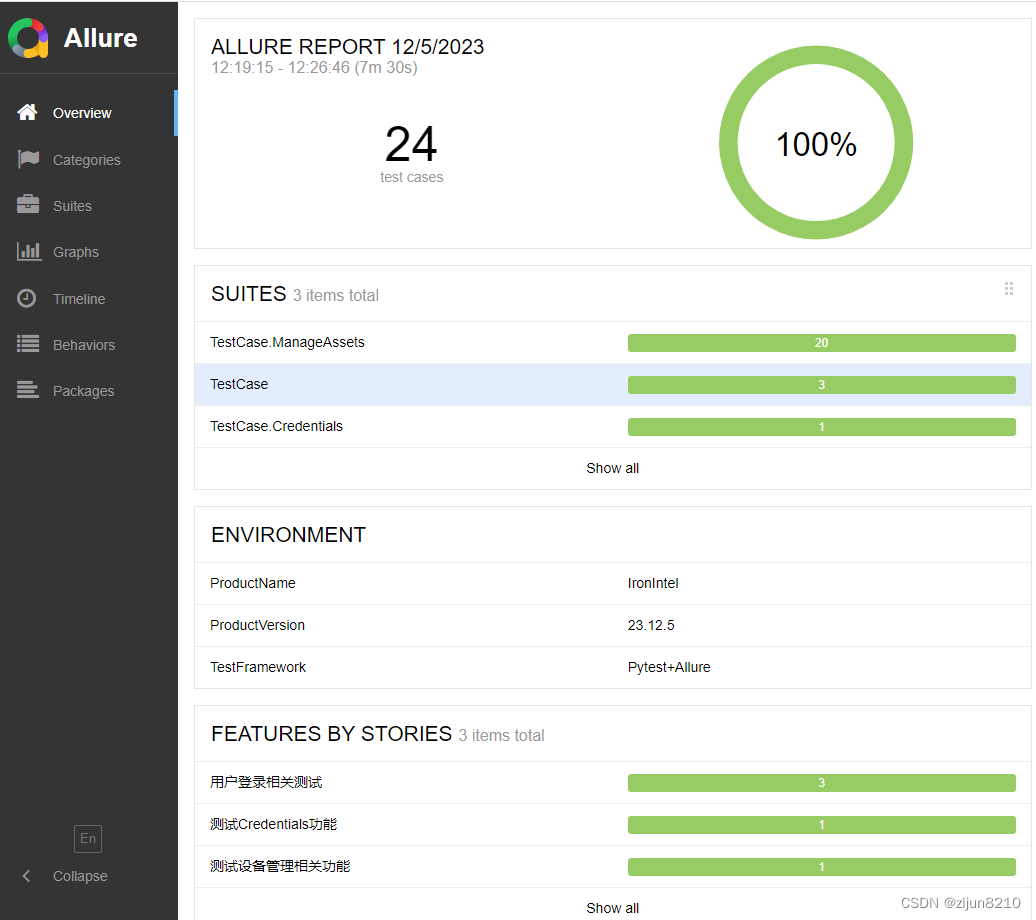
图
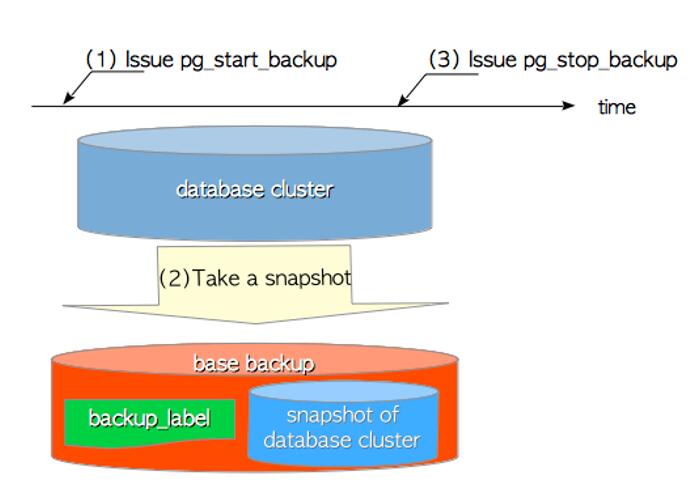
by.Qin3Yu
请注意:严格来说,图不是一种数据结构,而是一种抽象数据类型。但为了保证知识点之间的相关性,也将其列入数据结构专栏。
本文需要读者掌握顺序表和单链表的操作基础,若需学习,可参阅我的往期文章:
【C++数据结构 | 顺序表速通】使用顺序表完成简单的成绩管理系统.by.Qin3Yu
【C++数据结构 | 单链表速通】使用单链表完成数据的输入和返回元素之和.by.Qin3Yu
本文将不会涉及图的具体操作案例,若需阅读案例,可参阅我的往期文章:
【经典案例 | 骑士之旅】回溯算法解决经典国际象棋骑士之旅问题 | 详解Knight’s Tour Problem数学问题.by.Qin3Yu
【算法详解 | 最小生成树 I 】详解最小生成树prim算法(拓展kruskal算法) | 电力网络最短路径覆盖问题.by.Qin3Yu
文中所有代码默认已使用std命名空间且已导入部分头文件:
#include <iostream>
#include <vector>
using namespace std;
概念速览
图的基本概念及定义
- 图(Graph) 是由一组顶点和连接这些节点的边组成的数据类型,可以将图抽象的看作为一些岛屿和连接这些岛屿的小桥,顶点就是岛屿,边就是桥。点和边是构成图的基本元素,如下所示就是一个图:

- 注意:大多数数据结构和类型都可以为空,但是 图不可以为空 。
向性与连通性
- 在图中,如果 所有的边 都没有方向限制,均可以双向通行,则称为无向图。相反,如果 所有的边 都具有方向限制,每条边只提供单向通行,则称为无向图。

- 在 无向图 中,如果图上任意一对点都有路径连通(可以穿过其他点),则称为 连通图 。如果在 有向图 中,如果图上任意一对点都有路径连通且 双向连通 ,则称为 强连通图 。


特别注意:有向图需双向连通才算作强连通图!
加权图与边权
- 在很多图中,每条边都有指定的长度,且长度各不相同。在图论中,边的长度叫做 边权 ,每条边都有权值的图叫做 加权图 ,例如在下图中,图书馆到体育室的边的长度为1200m,则我们可以说图书馆-体育室的 边权 为1200:

稀疏图与稠密图
- 在图中,边数明显少于点数 的图叫做稀疏图,相反,点数明显少于边数 的图叫做稠密图。需要注意,稀疏图与稠密图只是一个相对而言的概念,没有明确的数值指明边和点之间的数量界限。

度与入度出度
- 在无向图中,某个点的 度指的是与这个点相连的边的数量。如图所示,我们可以说 A点 的度为 2,B点 的度为 1:

- 在有向图中,某个点的 入度是指与该点相连,且终点为该点 的边的数量。相反,某个点的* 出度是指与该点相连,且起点为该点* 的边的数量。如图所示,我们可以说 A点 的出度为 2,入度为 1:

一个明确的图应具有以下特征:
1. 无重复边: 在无向图中,每对点之间只有唯一的一条边连接,不存在一对点之间有两条边的情况;
2. 明确向性: 大多数情况下的图要么是有向图,要么是无向图,很少存在同一张图中某些边有向同时某些边无相(混合图)的情况;
3. 无自环: 在图中不存在连接一个节点到其自身的边。
图的存储与表示
图根据稀疏和稠密的特征有两种常用的存储方式,分别是邻接矩阵和邻接表。
邻接矩阵
- 在邻接矩阵中,我们使用一个二维数组(矩阵)来表示图,如下图中有6个点,则我们需要画一个6×6的矩阵,且默认表内元素全部为0:

int n = 6; // 点数
vector<vector<int>> Graph(n, vector<int>(n, 0)); // 初始化一个n×n的矩阵,默认为0
- 如图,点1 和 点0 之间有一条边连接,则我们在 (1,0) 位置填入 1 ,表示 点1 和 点0 之间有边:

- 同理,点1 和 点2 之间有一条边连接,则我们在 (2,1) 位置填入 1 ,表示 点2 和 点1 之间有边:

- 一直重复这个过程,我们便可以得出以下结果:

- 但同时根据无向表双向通行的特性,点0 到 点1 有边,那么反过来 点1 到 点0 也有边,所以我们还需要反过来再重复一次,将剩下的半部分补齐。如下图所示,可以看到 无向图的邻接矩阵呈对角线对称 ,所以我们在使用程序输入时可以直接 对称输入 :

for (int i = 0; i < n; i++) {
int x, y;
cin >> x >> y;
Graph[x][y] = 1;
Graph[y][x] = 1; // 对称输入
}
- 但如果图是有向图,则只能逐个输入:
int m = ... // 边数
for (int i = 0; i < m; i++) {
int x, y;
cin >> x >> y;
Graph[x][y] = 1;
}
- 从上面的案例可以看出邻接矩阵需要维护一个n×n的二维数组,且使用1来标记边的位置,所以不难看出,假如图是点很多而边很少的稀疏图,则会浪费大量的内存。所以,邻接矩阵更适合表示稠密图和无向图 。
邻接表
- 除了用矩阵外,我们还可以用多链表来表示图。在链表中,每个节点具有两个成员,一个为该节点的值,另一个为指向下一个节点的指针,我们先初始化一些链表,让每个点都有一串对应的链表来表示自己与其他点的相连关系:

//定义单链表
struct ListNode {
int val;
ListNode* next;
ListNode(int x) : val(x), next(nullptr) {}
};
const int n = 6; // 节点数
const int m = 7; // 边数
ListNode* Graph[n]; // 声明多个链表
- 如图,点0 与 点1 相连,则我们在 0号链表 上增加节点,节点值为 1,代表 点1:

- 然后再看 点1,点1 与 点2 相连,则我们在 1号链表 上增加节点,节点值为 2,代表 点2:

- 不断重复此过程,我们便可以得出如下的结果,这便是图的邻接表,与邻接矩阵相比,邻接表不需要维护一个很大的矩阵来表示边与边的关系,但是构造起来也相对复杂。因此,邻接表更适合表示稀疏图和有向图:

- 在具体的代码实现中,我们只需要将节点链接到链表后面即可,具体操作请参阅我的往期单链表教程,本文不再赘述:
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
ListNode* newNode = new ListNode(v);
newNode->next = Graph[u];
Graph[u] = newNode;
}
- 但要注意,在无向图中边是双向互通的,只要 u 有一条路径指向 v,那么相反 v 也有一条路径指向 u。因此,对于无向图,我们需要对称输入:
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
ListNode* newNode1 = new ListNode(v);
newNode1->next = Graph[u];
Graph[u] = newNode1;
ListNode* newNode2 = new ListNode(u);
newNode2->next = Graph[v];
Graph[v] = newNode2;
}
至此图的相关内容已讲解完毕,具体案例可以参阅我的往期文章(如文章开头所示)(=
如需提问,可以在评论区留言或私信(=
完整代码展示
无向图邻接矩阵

代码
#include <iostream>
#include <vector>
using namespace std;
int n = 6; // 点数
int m = 7; // 边数
vector<vector<int>> Graph(n, vector<int>(n, 0));
int main() {
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
Graph[u][v] = 1;
Graph[v][u] = 1;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
cout << Graph[i][j] << " ";
cout << endl;
}
return 0;
}
参考输入
0 1
1 2
2 3
3 4
4 0
2 5
3 5
参考输出
0 1 0 0 1 0
1 0 1 0 0 0
0 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 0 1 1 0 0
有向图邻接矩阵

代码
#include <iostream>
#include <vector>
using namespace std;
int n = 6; // 点数
int m = 7; // 边数
vector<vector<int>> Graph(n, vector<int>(n, 0));
int main() {
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
Graph[u][v] = 1;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
cout << Graph[i][j] << " ";
cout << endl;
}
return 0;
}
参考输入
0 1
1 2
2 3
3 4
4 0
3 5
5 3
参考输出
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 1
1 0 0 0 0 0
0 0 0 1 0 0
无向图邻接表

代码
#include <iostream>
using namespace std;
struct ListNode {
int val;
ListNode* next;
ListNode(int x) : val(x), next(nullptr) {}
};
const int n = 6; // 节点数
const int m = 7; // 边数
ListNode* Graph[n];
int main() {
for (int i = 0; i < n; i++)
Graph[i] = nullptr;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
ListNode* newNode1 = new ListNode(v);
newNode1->next = Graph[u];
Graph[u] = newNode1;
ListNode* newNode2 = new ListNode(u);
newNode2->next = Graph[v];
Graph[v] = newNode2;
}
for (int i = 0; i < n; i++) {
cout << i << ": ";
ListNode* curr = Graph[i];
while (curr != nullptr) {
cout << curr->val << " ";
curr = curr->next;
}
cout << endl;
}
return 0;
}
参考输入
0 1
1 2
2 3
3 4
4 0
2 5
3 5
参考输出
0: 4 1
1: 2 0
2: 5 3 1
3: 5 4 2
4: 0 3
5: 3 2
有向图邻接表

代码
#include <iostream>
using namespace std;
struct ListNode {
int val;
ListNode* next;
ListNode(int x) : val(x), next(nullptr) {}
};
const int n = 6; // 节点数
const int m = 7; // 边数
ListNode* Graph[n];
int main() {
for (int i = 0; i < n; i++)
Graph[i] = nullptr;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
ListNode* newNode = new ListNode(v);
newNode->next = Graph[u];
Graph[u] = newNode;
}
for (int i = 0; i < n; i++) {
cout << i << ": ";
ListNode* curr = Graph[i];
while (curr != nullptr) {
cout << curr->val << " ";
curr = curr->next;
}
cout << endl;
}
return 0;
}
参考输入
0 1
1 2
2 3
3 4
4 0
3 5
5 3
参考输出
0: 1
1: 2
2: 3
3: 5 4
4: 0
5: 3
感谢您的观看(=
by.Qin3Yu