一、频域在图像中的应用

1.图像增强与图像去噪
绝大部分噪音都是图像的高频分量，通过低通滤波器来滤除高频——噪声;  边缘也是图像的高频分量，可以通过添加高频分量来增强原始图像的边缘；
2.图像分割之边缘检测
提取图像高频分量
3.图像特征提取：
形状特征：傅里叶描述子
纹理特征：直接通过傅里叶系数来计算纹理特征
其他特征：将提取的特征值进行傅里叶变换来使特征具有平移、伸缩、旋转不变性
4.图像压缩
可以直接通过傅里叶系数来压缩数据；常用的离散余弦变换是傅立叶变换的实变换；

     低频代表图像中的渐变，它们包含最多的信息，因为它们决定了图像中的整体形状或模式。高频对应于图像中的突然变化，它们在图像中提供更多的细节。

二、傅里叶变换在图像中的显示

       如果输入二维图像数据，则显示的图像是输入的灰度分布，傅立叶频谱是输入的频率分布，频谱图中心对称。图像频谱即二维频谱图通过对原图像进行水平和竖直两个方向的所有扫描线处一维傅立叶变换的叠加得到。

      频谱图中心代表的是低频，往四面八方扩展后逐渐变为高频，并且左上-右下、右上-左下完全对称。其中黑色部分即表明该图像不含有该部分的频率，相反颜色越亮，代表该频率的幅值越高。通常我们会发现中心处是最亮的，即低频信号是最多的，这也和原时域图的信息是匹配的。

 

                                                            原始图像

                                                         没有移位的傅里叶变换图像

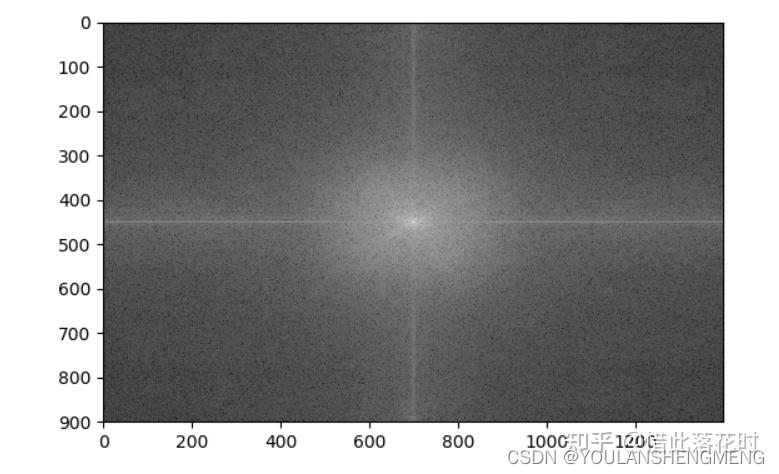                                      移位后的图像，移位是为了将零频率成分移到图像的中心 

在傅立叶域中，中心区域代表低频分量，外围区域代表高频分量，图像的中心代表零频率的直流值，即图像的总强度。其中频域中的每个点都是根据整个空间图像计算的。

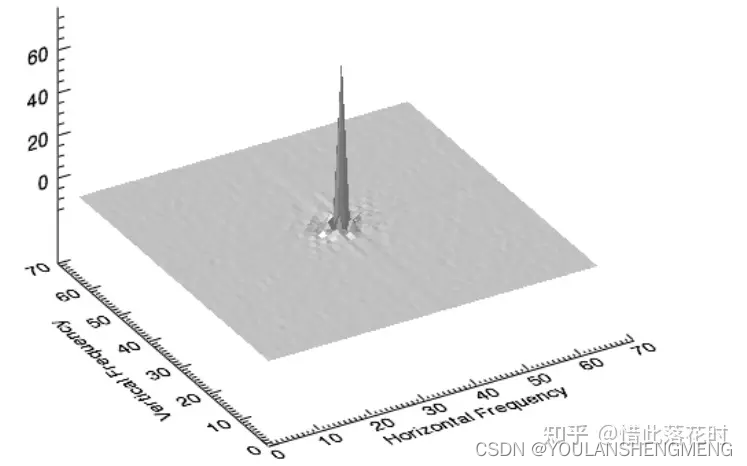
2.1二维图像和频谱图的关联

        关于频谱图，通常其图像size 和原时域图相同，但其(u, v)坐标和原图的(u, v)坐标并没有一一对应的关系。为了尽可能直观描述图像和频谱图的关联，下图描绘了一个只有一行像素的图像和其频谱图的示意图（事实上下图并不严谨，但足以让我们对频谱图不再那么陌生）。以此为扩展，我们便能更加直观的理解在二维图像里，各个方向的频率和图像的关联关系了。

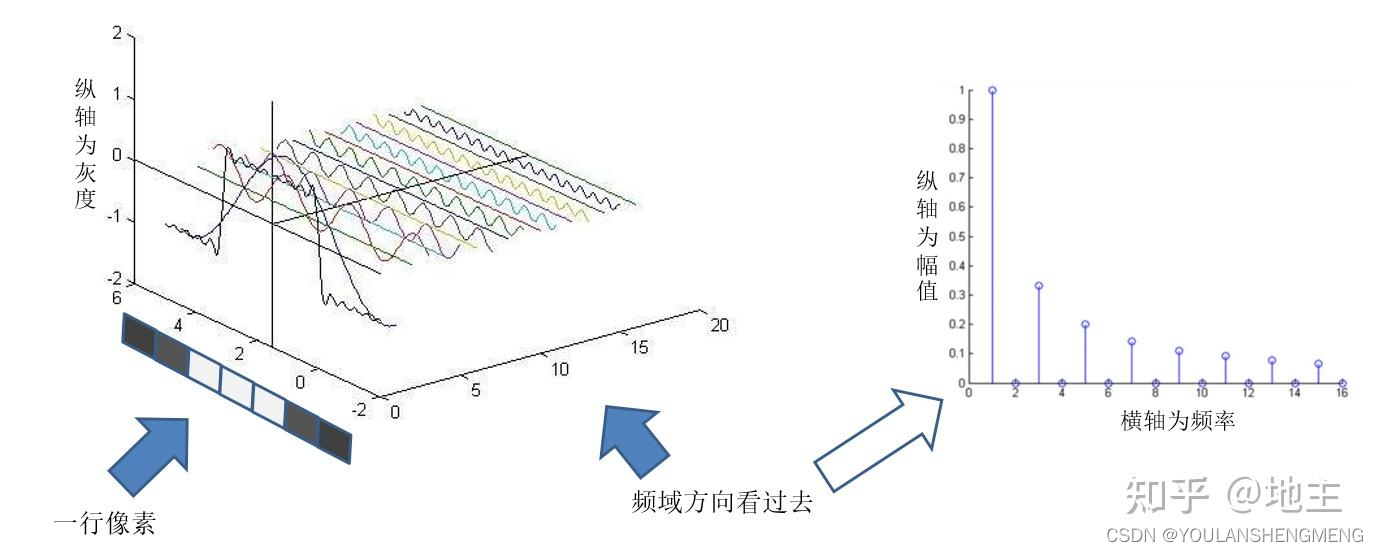
我们从单个点的频率开始，来分析一下频谱图和原图是如何关联的。

DC(低频)，也被叫做傅里叶变换的基底，它代表图中最平滑的区域，它的值等于原图的平均亮度值。其他的各频段的正弦波信号均是在该值的基础上叠加的。假设一张图没有任何梯度，即完全平滑，那么它的傅里叶谱图长什么样呢：

        我们看到，上图1时域图是纯黑色，对应的频谱图也是纯黑色（说明基底也等于0）；上图2时域图是灰色，对应的频谱图除了基底是一个灰点外，其他频段都为0；同样的上图3时域图是纯白色，频谱图得到相对更亮的基底。说明对于一张没有梯度的图，只存在低频信息，严格的说是周期无限大、频率无限小。我们回忆一下上面描述的一维傅里叶变换对于周期矩形的公式表示，即此时只存在A/2的分量，其他分量均为0。

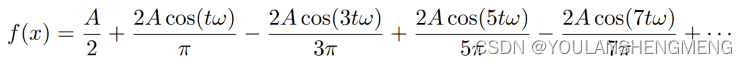
 接下来我们再看下面的图：

我们可以发现，上图第一行的时域图，均是X 方向上的正弦分布的灰度图，且从左向右频率越来越高，同时对应于第二行的频谱图，我们可以发现四个信息：

1. 只有2个点（对称关系，实则即1个点）
2. 随着频率越高，亮点离中心点的距离越远
3. 亮点在频谱图的x方向上，与时域图正弦分布的方向一致
4. 基底为0，对应于时域图的平均亮度也为0

        这时，我们应该可以确定，频谱图上一个点对应于一张呈正弦分布的时域图，其亮度值代表其幅值（如果亮度为0，幅值也为0 ，则不会对原图有任何的贡献也不会有任何的影响）；其正弦分布的方向与点在频谱图上相对于中心点的方向也是一一对应的。如下面的图，正弦方向从上向下展开，对应于的频谱图上的点也在Y 方向上；如果频谱图上的点相对于中心点有一定角度，对应的时域正弦图像也有一定的角度。

另外，有一点我们还需要提及，那就是频谱图中不包含相位信息，相位信息有专门的相位图来表示。如下图：

 

       图中最右方的三张图即是相位图。除此之外我们应该能发现，频谱图内容会随着时域图的角度不同而有所不同，但不会随着原图的平移而产生不同；但对相位图而言，无论原图有旋转还是平移，都会出现变化。 

      最后，我们再回到图像的时域-频域对应关系。我们已经知道频谱图上每一个点均代表一个固定频率、幅值、相位的正弦波图像，那么抛开频谱图上幅值为0 的点外，其他的所有点都映射着一张正弦图。而傅里叶级数告诉我们，任何一条连续函数，都可以用多个正弦周期函数叠加而成，或者我们直接映射二维傅里叶（反）变换公式：

即我们把所有的正弦图(F(w))叠加在一起，便能够恢复出原始的时域图。我们再来看下面这张图，假设频谱图中有1000个值不为0 的亮点，那么它们会生成1000张固定频率、幅值和相位的正弦图像，把这一千张图像加在一起（包括基底的图），我们就能得到左边的原图。

 

2.2  频谱图的意义

       接下来我们可以进一步思考，得到频谱图后有什么意义呢？从上面的描述我们知道，图像的傅里叶变换和反变换，就是将一张图从时域转换为频域再转换回时域的过程，最终时域才是我们的目标。因此将图像变换到频域后，可以供我们做一些与频率相关的事情后再转回时域。如滤波，见下图：

上图为原始图片的时域和频域图，下图为我们将低频信号的幅值变为0后的时域-频域图（相信我们应该可以快速的get 到下面右边的频谱图是如何变成左边的时域梯度图的了）

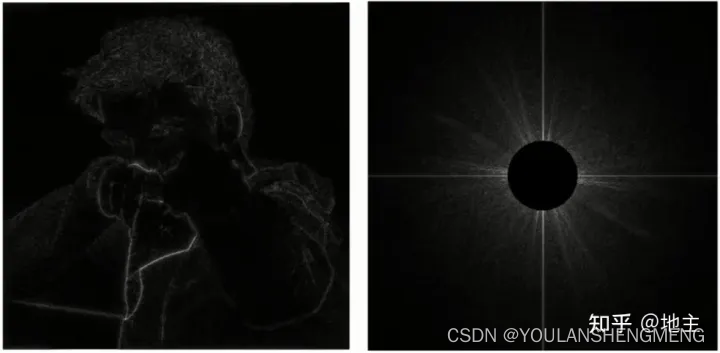
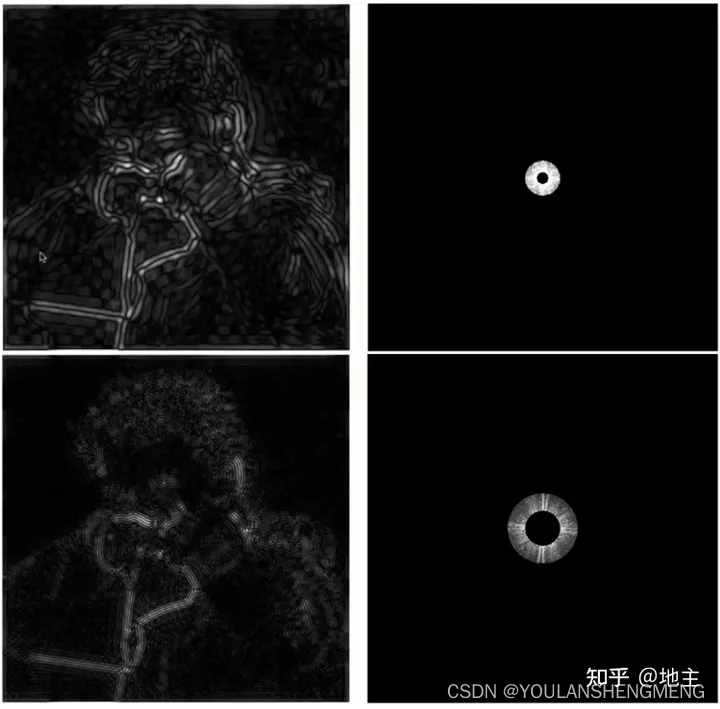
      下图为保留低频信息，滤除高频信息的图。这里我们应该会想到时域的卷积运算，通过对原图做一次卷积如Box Filter 或者高斯滤波等，不也可以得到类似的结果吗。是的，通过卷积运算我们可以得到一张模糊的图，上面的高频也一样可以通过索贝尔滤波、拉普拉斯滤波得到只保留边界的图；但卷积的本质仍然是通过消除图像的高频或者低频信息，保留另外的频率成分的结果。

那么带通滤波器同样也会得到应有的结果，可以理解在频域里得到这样的图片，比在时域里去对图像做变换得到这样的图片要简单很多。

2.3 傅里叶变换与反变换：空域卷积-频域乘积

下面以Box Filter 为例，来分析一下在空域和频域滤波的关系。见下图，已知空域的卷积恒等于频域的乘法（反之一样），那么我们重点看下方的频域乘法，即两张频谱图对应点的乘积，变成了等号右边的频谱图，我们可以发现等号右边的频谱图相比左边的频谱原图，发生了很大的变化，特别是高频的区域都变成了黑色，其等号右边的图很像上方右边的频谱图，即只有低频部分有幅值。

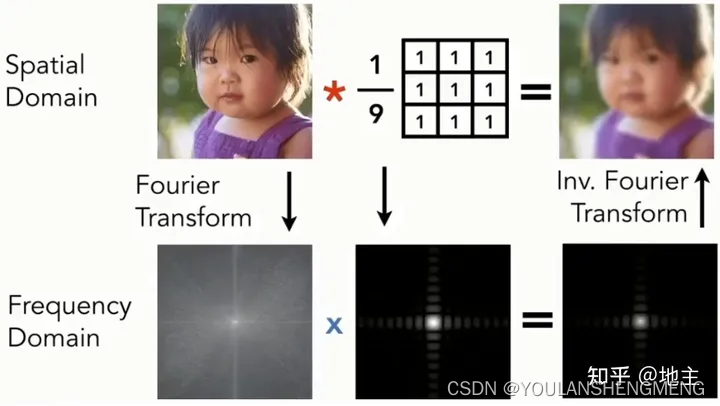
另外补充一点关于卷积核的频谱图。如下图，卷积核的频谱图即是构建一张中间3*3区域为白色幅值，其他部分为0幅值的图，对其进行傅里叶变换，得到右边的频谱图。 

如果我们将3*3扩大后，其对应关系也会发生如下的变化。相比上面的频谱图，下面的频谱图拥有更少的高频信息，用该图和原图的频谱图做乘法，可以获得更为模糊的图像，这和我们用7*7的卷积核比用3*3的卷积核做卷积可以得到更模糊的图像是一个道理。