Private Set Intersection from Pseudorandom CorrelationGenerators 最快PSI！导览解读

一、概述

二、相关介绍

三、性能对比

四、技术细节

1.KKRT

2.Pseudorandom Correlation Generators

3.A New sVOLE-Based BaRK-OPRF

4.BaRK-OPRF

五、总结

参考文献

一、概述

这篇文章的主要脉络和核心思想是探讨如何利用伪随机相关生成器（PCG）改进私有集合交（PSI）协议。文章首先介绍了PCG的概念和作用，然后阐述了如何将PCG与分布式密钥生成协议相结合，以实现长伪随机相关性的高效生成。接着，文章重点讨论了PCG对私有集合交协议的改进作用，提出了两个主要结果：高度优化的半诚实PSI协议和利用PCG实现新相关性的协议。这些结果展示了PCG在安全计算应用中的潜在价值，为提高协议效率和性能提供了新的思路和方法。

这篇文章的突破包括： 1. 针对私有集合交（PSI）协议，提出了高度优化的半诚实PSI协议，实现了竞争性的通信和显著的性能改进。 2. 利用PCG实现新相关性的协议，在标准模型下实现了全面的恶意安全性，且在通信和性能方面具有竞争优势。 3. 发现了Cuckoo hashing-based协议在PCG方面的优势，以及对KKRT协议的深入优化，使得通信复杂度完全独立于计算安全参数，为协议的进一步优化提供了新的可能性。这些突破为安全计算应用中的私有集合交协议带来了新的发展方向和性能提升。

二、相关介绍

目前主流的实现隐私求交PSI的关键技术包括：Key exchange-based、Cuckoo hashing-based、OKVS、Polynomial manipulation.

其中，基于密钥交换的早期PSI协议使用Diffie-Hellman密钥交换技术，通信复杂度相对较低，但需要为每个项目计算多个指数，性能相对较差。基于Cuckoo哈希的PSI协议是过去几十年中最常用的PSI协议之一，通常与快速的无意识传输扩展相结合。最近，基于OKVS的PSI协议已经超越了基于Cuckoo哈希的协议，但是KKRT协议仍然是最具竞争力的PSI协议之一。基于多项式操作的PSI协议将数据集表示为有限域上的多项式，并通过对这些多项式进行操作来计算集合操作。虽然这些协议通常比基于Cuckoo哈希或OKVS的协议慢得多，但它们具有一些优点，例如实现更强的功能（如阈值私有集合交[GS19]）并在标准模型下提供安全性。

当然还有文章的“主角”：seudorandom correlation generators.在现代安全计算协议中，安全共享相关随机字符串是一个关键组成部分，PCG可以在几乎没有通信的情况下实现这个功能。PCG还可以用于构建无声无意识传输扩展协议，这些协议可以使用最小的（对数级别的）通信实现（伪随机）OT扩展。由于最高效的PSI协议依赖于高效的OT扩展，因此使用基于PCG的技术来提高其效率是一个自然的想法。最近，这种方法已经在基于OKVS的PSI协议中得到了应用，导致了迄今为止最有效的PSI协议[RS21]。基于OKVS的PSI协议现在已经牢固地确立为该领域的主导范式，使用PCG来进一步减少其通信开销似乎进一步扩大了与其他范式之间的差距。

三、性能对比

四、技术细节

1.BaRK-OPRF

这里Alice将获得所有数据伪随机数，并且Bob将获得所有种子。上面这个协议若基于OTE将十分高效的实践，但是当其应用到隐私求交时，我们需要注意Bob会将所有数据计算对应的伪随机函数并发送给Alice，其中的传输量将与Bob的数据量相关。当Bob的数据量较大时，需要发送整个数据集给Alice，传输开销“难以接受”。

引入Cuckoo Hash见小通信和计算开销

为了获得PSI协议，KKRT使用哈希将数据集映射到桶中。使用简单的哈希策略，对于大小为n的数据集，每个桶中最多只能有log n / log log n个项，这仍会导致显着的开销，因为必须比较同一桶中Alice和Bob的所有项对。

2.Pseudorandom Correlation Generators

PCG 是近年 MPC 研究的热点，它的本质是通过“短的种子”生成“长的随机串”（即相关随机数）。而在 MPC 应用中，“离线”阶段不再需要存储大量的相关随机数，而只需要存储少量的 PCG 种子。当“在线”阶段需要消耗相关随机数时，各方不需要任何交互，可以直接通过 PCG 种子产生所需的相关随机数。

两方的伪随机相关生成器由 PCG.Gen 和 PCG.Extend 两个算法构成，其中 PCG.Gen 可以由可信第三方或两方协议实现 [BCGI18][BCG+19b]。

● 随机算法，给定安全参数，输出一对种子。

● 确定性算法，给定及种子，输出伪随机串，并且满足。

3.vector OLE

看图中实现的效果，Alice将获得u和v，Bob将获得∆和w，并满足最后的条件。本文的将要使用vole代替oprf，或者说使用vole版的oprf。w、v、u均为向量。

Alice发送z=x-u给Bob，并且自身计算 H(i,v_i) 即可，

Bob计算(k1, · · · , kn) = ∆ · z + w， $F_{\Delta, k_i}(y)=H(i, k_i-\Delta y)$ 。

正确性验证：

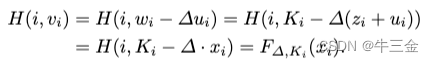
为什么使用VOLE实现OPRF。

1. 高效性：VOLE协议可以高效地生成伪随机相关性，这对于实现OPRF协议是非常重要的。通过使用VOLE，可以在保持安全性的同时，实现高效的协议，这对于实际应用中的性能至关重要。近年来VOLE非常火热的安全协议，将带来效率的大幅度提升。
2. 隐私保护：VOLE协议允许两方计算他们的输入的线性函数，同时不泄露有关输入的任何信息。这种隐私保护特性对于构建安全的OPRF协议至关重要，因为它确保了参与方的输入保持私密。
3. 安全性：VOLE协议提供了安全的计算环境，确保了计算的正确性和隐私性。这对于构建安全的OPRF协议是至关重要的，因为OPRF协议需要在不暴露输入的情况下进行计算。因此，使用sVOLE来实现OPRF可以同时保证高效性、隐私保护和安全性，使得OPRF协议在实际应用中更加可行和可靠。

五、总结

本文介绍了向量OLE和sVOLE在实现OPRF协议中的重要性和应用。向量OLE是一种密码学原语，允许两个参与方计算它们各自输入向量的内积，同时不泄露有关它们个体输入的任何信息。sVOLE是一种基于子域的向量OLE协议，可以高效地生成伪随机相关性，同时保护参与方的隐私。 OPRF是一种重要的密码学原语，用于在不暴露输入的情况下计算伪随机函数。使用sVOLE来实现OPRF协议可以同时保证高效性、隐私保护和安全性，使得OPRF协议在实际应用中更加可行和可靠。本文还介绍了一些相关的研究成果和技术，包括私有集合交集协议、安全多方计算、Cuckoo hashing-based协议等。这些技术和成果都与向量OLE和sVOLE密切相关，为实现安全、高效的计算提供了重要的支持和保障。总之，向量OLE和sVOLE在实现OPRF协议中具有重要的应用和意义，可以为实现安全、高效的计算提供重要的支持和保障。

参考文献

相关资料——https://download.csdn.net/download/niujinya/88610168

[BC22] Private Set Intersection from Pseudorandom Correlation Generators

[GS19] S. Ghosh and M. Simkin. The communication complexity of threshold private set intersection.In CRYPTO 2019, Part II, LNCS 11693, pages 3–29. Springer, Heidelberg, August 2019.

[RS21] P. Rindal and P. Schoppmann. VOLE-PSI: Fast OPRF and circuit-PSI from vector-OLE. LNCS,pages 901–930. Springer, Heidelberg, 2021

[KKRT16] V. Kolesnikov, R. Kumaresan, M. Rosulek, and N. Trieu. Efficient batched oblivious PRF with applications to private set intersection. In ACM CCS 2016, pages 818–829. ACM Press, October 2016.

[KRTW19] V. Kolesnikov, M. Rosulek, N. Trieu, and X. Wang. Scalable private set union from symmetric-key techniques. In ASIACRYPT 2019, Part II, LNCS 11922, pages 636–666. Springer, Heidelberg, December 2019.

[CM20] M. Chase and P. Miao. Private set intersection in the internet setting from lightweight oblivious PRF. In CRYPTO 2020, Part III, LNCS 12172, pages 34–63. Springer, Heidelberg, August 2020.

[PRTY20] B. Pinkas, M. Rosulek, N. Trieu, and A. Yanai. PSI from PaXoS: Fast, malicious private set intersection. In EUROCRYPT 2020, Part II, LNCS 12106, pages 739–767. Springer, Heidelberg, May 2020.

[GPR+21] G. Garimella, B. Pinkas, M. Rosulek, N. Trieu, and A. Yanai. Oblivious key-value stores and amplification for private set intersection. LNCS, pages 395–425. Springer, Heidelberg, 2021.

[CRR21] G. Couteau, P. Rindal, and S. Raghuraman. Silver: Silent VOLE and oblivious transfer from hardness of decoding structured LDPC codes. LNCS, pages 502–534. Springer, Heidelberg, 2021.