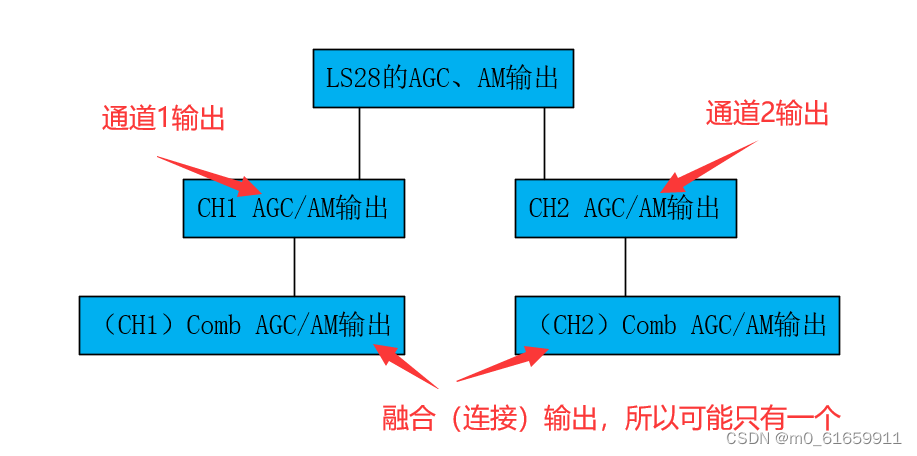
这个标题涉及到一个复杂系统的问题,以下是对标题的解读:
-
电–气–交通网络耦合系统:
- 涉及电力系统、气体(可能是天然气)系统和交通网络之间的相互关系。这种耦合可能表示这些系统之间存在一定的依赖和相互影响。
-
多重不确定性:
- 指这个系统面临多方面的不确定性。这可能包括来自天气、需求波动、交通状况等多个方面的不确定性因素。
-
数据驱动:
- 意味着该系统的优化和调度过程将依赖于实时或历史数据的分析和应用。数据可能来自各个系统组件的监测、传感器、或其他数据源。
-
鲁棒优化调度:
- 表示在考虑到不确定性的情况下,对系统进行优化和调度。"鲁棒"表示系统对不确定性有一定的适应性和稳健性,能够在面对不确定性时依然保持高效性能。
综合起来,这个标题表明研究的焦点是在电力、气体和交通这三个系统相互作用的复杂背景下,通过利用数据进行驱动,设计一种能够在多重不确定性条件下稳健优化调度的方法。这种研究可能有助于提高系统的可靠性和效率,特别是在面临实时和未知变化的环境中。
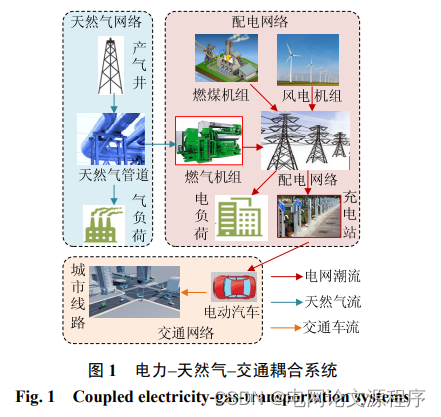
摘要:电力、天然气、交通等不同能量流网络的深度耦合和良性互动,对多元化综合能源系统的协同优化运行提出了极大挑战。针对电–气–交通网络耦合系统中的多重不确定性因素,提出综合考虑交通流量、风电出力及燃气机组耗气不确定性的数据驱动鲁棒协同优化调度模型。首先,依据Wardrop用户均衡准则获取交通网络的最优流量分配,并根据网络耦合约束将交通、气网络的不确定性转化到配电网统一考虑;其次,结合风电出力和交通流量的历史数据构造高维源、荷不确定量的模糊集表征其概率分布特性;然后,以基准预测场景下日前运行成本和不确定量最劣场景分布下实时调整成本最小为目标,建立基于数据驱动的两阶段鲁棒经济调度模型,在主、子问题协同求解框架下采用列约束生成方法进行求解。最后,通过算例验证了所提模型及求解方法的有效性。
这段摘要描述了针对电力、天然气和交通等多个能源流网络之间的深度耦合和良性互动所带来的协同优化运行挑战的问题。为了应对电-气-交通网络中的多重不确定性因素,提出了一种数据驱动的鲁棒协同优化调度模型。
具体而言,这个模型首先根据Wardrop用户均衡准则获取了交通网络的最优流量分配。然后,通过将交通和气网络的不确定性转化为配电网中统一考虑的网络耦合约束,有效地处理了不同网络之间的复杂关系。其次,结合了风电出力和交通流量的历史数据,构建了高维源、荷不确定性的模糊集,用于表示它们的概率分布特性。
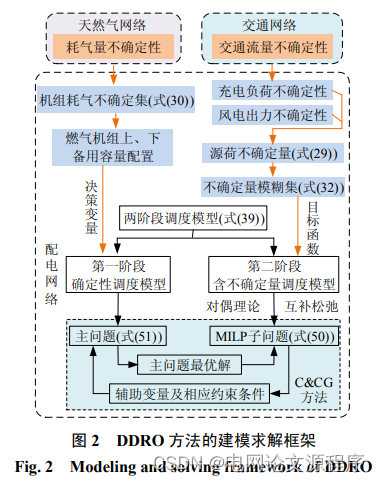
接下来,提到了基于数据驱动的两阶段鲁棒经济调度模型。在这个模型中,以基准预测场景下的日前运行成本和在不确定量最劣场景分布下实时调整成本最小为目标。这个模型采用了主、子问题协同求解框架,使用列约束生成方法进行求解。
最后,通过算例验证了所提出的模型及求解方法的有效性。这可能包括对不同场景下的系统运行进行模拟,以证明该模型在处理多元化综合能源系统的协同优化运行方面的实际效果。
关键词:电-气-交通耦合系统;多重不确定性;模糊集;数据驱动;鲁棒优化;
-
电-气-交通耦合系统: 这表示在这个研究中,电力系统、天然气系统和交通系统被看作是一个紧密耦合的整体。这意味着它们之间存在相互依赖和影响,而不是孤立地运行。这种综合系统的研究涉及到这些不同领域之间的相互作用和协同优化。
-
多重不确定性: 指在研究的系统中,存在多个不确定的因素或变量。这些因素可能包括但不限于难以准确预测的变化、外部环境的波动等。在电-气-交通耦合系统中,这可能涉及到电力需求、风电出力、交通流量等多个方面的不确定性。
-
模糊集: 表明研究中采用了模糊集理论来处理系统中的不确定性。模糊集是一种数学工具,用于描述不确定性和模糊性。在这里,它可能被用来建模历史数据中的风电出力和交通流量的概率分布特性,以更好地理解系统的行为。
-
数据驱动: 表示该研究采用了数据作为研究的主要驱动力。这可能包括对历史数据的分析和利用,以建立模型、预测系统行为或进行优化。数据驱动方法通常侧重于通过大量实际数据来指导决策和建模。
-
鲁棒优化: 表示在系统设计或决策中考虑到不确定性,以确保系统在面对多样化和变化的情况时仍能保持稳健性。鲁棒优化方法旨在使系统对于输入变化或不确定性具有抵抗力,而不是过于依赖于特定的预测或参数。
这些关键词的结合表明研究的重点在于如何通过考虑多重不确定性、采用模糊集理论和数据驱动方法,以及应用鲁棒优化原则,来优化电-气-交通耦合系统的运行。这可能包括对系统的调度、流量分配和成本优化等方面的研究。
仿真算例:本文选取改进的 IEEE-33 节点配网,7 节点天 然气网络和 12 节点交通网络构建耦合系统。网络 拓扑结构见附图 C1—C2,常规电力、气负荷见附 图 C3,配网中机组运行参数见附表 C1,发电成本 参数见文献[20],其他设备参数见文献[24]。交通、 气网络运行参数分别见文献[7]和文献[20]。风电出 力预测误差数据来源于文献[29],其装机容量均为 1.5MW。参照文献[20]假定交通网络车流量服从正 态分布,并将各时段车流量变化范围设置为0.8-1.2q。本文算例均在 Matlab 平 台下调用 CPLEX12.6 求解器进行计算。
仿真程序复现思路:
复现上述仿真需要考虑以下步骤,并以Matlab为例来表示:
- 构建网络拓扑:
- 从附图 C1—C2 中获取改进的 IEEE-33 配网、7 节点天然气网络和 12 节点交通网络的拓扑结构。
- 根据文献[7]和文献[20]获取网络节点和边的信息,以建立各网络的拓扑表示。
% 以Matlab为例,使用图数据结构表示网络拓扑
% 以下是一个简化的示例,实际情况需要根据附图和文献中提供的数据进行详细构建
% 配电网拓扑
powerNetwork = graph(...); % 根据 IEEE-33 数据构建图
% 天然气网络拓扑
gasNetwork = graph(...); % 根据 7 节点天然气网络数据构建图
% 交通网络拓扑
trafficNetwork = graph(...); % 根据 12 节点交通网络数据构建图
- 设定系统参数:
- 从文献[20]和文献[24]中获取电力系统的机组运行参数、发电成本参数,以及其他设备参数。
- 从文献[7]和文献[20]中获取天然气网络和交通网络的运行参数。
% 电力系统参数
powerGenerationParameters = ...; % 从附表 C1 和文献[20]中获取
% 天然气网络参数
gasNetworkParameters = ...; % 从文献[7]和文献[20]中获取
% 交通网络参数
trafficNetworkParameters = ...; % 从文献[7]和文献[20]中获取
- 加载风电出力预测误差数据:
- 从文献[29]中获取风电出力预测误差数据,确保装机容量为1.5MW。
% 风电出力预测误差数据
windPowerErrorData = ...; % 从文献[29]中获取
windPowerCapacity = 1.5; % 装机容量为1.5MW
- 模拟交通网络车流量:
- 参照文献[20]假定交通网络车流量服从正态分布,并将各时段车流量变化范围设置为0.8-1.2q。
% 交通网络车流量模拟
meanTrafficFlow = ...; % 此处设置正态分布的均值
stdDevTrafficFlow = ...; % 此处设置正态分布的标准差
% 生成正态分布随机数,表示车流量
trafficFlow = normrnd(meanTrafficFlow, stdDevTrafficFlow, 1, numberOfTimePeriods);
% 将车流量限制在0.8-1.2q的范围内
trafficFlow = max(0.8 * trafficFlow, min(1.2 * trafficFlow, trafficFlow));
- 调用CPLEX求解器进行计算:
- 使用Matlab中的CPLEX接口调用求解器进行系统优化计算。
% 调用 CPLEX12.6 求解器进行计算
% 假设已经定义了系统的优化问题和约束条件
% 创建 CPLEX 问题对象
problem = ...; % 创建优化问题
% 使用 CPLEX 12.6 求解器求解问题
solution = solve(problem);
通过以上步骤,你可以在Matlab平台上复现文中描述的仿真。注意,实际的实现需要更具体的数据和参数,并可能涉及更复杂的优化模型的构建。此外,确保你的Matlab环境中已经安装了CPLEX求解器,并正确配置了接口。