扩展卡尔曼滤波技术（Extended Kalman Filter，EKF）

一、概念介绍

卡尔曼滤波是一种高效率的递归滤波器(自回归滤波器), 它能够从一系列的不完全包含噪声的测量中，估计动态系统的状态，然而简单的卡尔曼滤波必须应用在符合高斯分布的系统中。

扩展卡尔曼滤波就是为了解决非线性问题，普通卡尔曼滤波只能应用于线性空间的问题。当系统为线性高斯模型时，滤波器能给出最优的估计，但是实际系统总是存在不同程度的非线性，如平方、三角关系、开方等。对于非线性系统，可以采用的一种方法是通过线性化方法将非线性系统转换为近似的线性系统，即为EKF，核心思想是：围绕滤波值将非线性函数展开成泰勒级数并略去二阶及以上项，得到一个近似的线性化模型，然后应用卡尔曼滤波完成状态估计。

卡尔曼滤波是贝叶斯滤波的一个特例。（当贝叶斯滤波中系统状态的置信度分布符合高斯分布时，贝叶斯滤波=卡尔曼滤波）

二、数学表达

系统定义为：

线性运动方程： $x_k=Ax_{k-1}+Bv_k+Gw_k,k=1,\ldots,K$
非线性运动方程： $x_k=f(x_{k-1},v_k)+w_k$
线性观测方程： $y_k=C_kx_k+n_k,k=1,\ldots,K$
非线性观测方程： $y_k=h(x_k)+n_k$
初始条件： $x_0\sim N(\check{x_0},\check{P_0}),w_k\sim N(0,Q),n_k\sim N(0,R)$

并使用 $\check{\left ( \cdot \right )}$ 表示先验， $\hat{\left ( \cdot \right )}$ 表示后验（即最佳估计值）。

1、线性卡尔曼滤波

预测

先验状态估计：

$\check{x}=A\hat{x_{k-1}}+Bv_k$

先验误差协方差：

$\check{P_k}=\hat{AP_{k-1}A^T}+GQG^T$

校正

卡尔曼增益：

$K_k=\check{P}_kC_k^T(C_k\check{P}_kC_k^T+R)^{-1}$

更新

更新后验状态估计：

$\hat{x_k}=\check{x_k}+K_k(y_k-C_k\check{x_k})$

更新后验误差协方差：

$\hat{P_k}=(I-K_kC_k)\check{P_k}$

2、扩展卡尔曼滤波

非线性方程线性化

非线性的状态方程和观测方程表示为如上所示，符合正态分布的噪声数据在经过非线性转换后不再是正态分布的随机变量了，此处使用近似处理：假设噪声符合上述正态分布，而且它们为相互独立、正态分布的白噪声(即把噪声从非线性函数中拿出来)。在后续的线性化过程中，这部分因为以上近似而产生的偏差会得到恢复 (近似地恢复) 。

对以上非线性方程(状态方程和观测方程)进行线性化，具体方法为一阶泰勒展开，忽略高阶项：

$x_k\approx\check{x}_k+A_{k}(x_{k-1}-\hat{x}_{k-1})+W_kw_k$
$y_k\approx\check{y}_k+H_k(x_k-\check{x}_k)+V_kv_k$

其中：
$A_k$ 为 $k$ 时刻 $f$ 对 $x$ 的雅克比矩阵；

$H_k$ 为 $k$ 时刻 $h$ 对 $x$ 的雅克比矩阵；

$W_k$ 为 $k$ 时刻 $f$ 对 $w$ 的雅克比矩阵；

$V_k$ 为 $k$ 时刻 $h$ 对 $\upsilon$ 的雅克比矩阵。

$\begin{aligned}&A_{k}=\frac{\partial f(x_{k-1},v_k,w_k)}{\partial x_{k-1}}|_{\hat{x_{k-1}},v_k,0} \\&H_k=\frac{\partial h(x_k,n_k)}{\partial x_k}|_{\check{x_k},0} \\&W_{k}=\frac{\partial f(x_{k-1},v_k,w_k)}{\partial w_{k-1}}|_{\hat{x_{k-1}},v_k,0} \\&V_k=\frac{\partial h(x_k,n_k)}{\partial v_k}|_{\check{x_k},0} \end{aligned}$

预测

先验状态估计：

$\check{x}=f(\hat{x_{k-1}},v_k,0)$

先验误差协方差：

$\check{P_k}=A_{k}\hat{P_{k-1}}A_{k}^T+W_{k}QW_{k}^T$

校正

卡尔曼增益：

$K_k=\check{P}_kH_k^T(H_k\check{P}_kH_k^T+V_{k}RV_{k}^T)^{-1}$

更新

更新后验状态估计：

$\hat{x_k}=\check{x_k}+K_k(y_k-h(\check{x_k},0))$

更新后验误差协方差：

$\hat{P_k}=(1-K_kH_k)\check{P_k}$

三、应用总结

滤波器针对的问题是如何通过数据来估计自身状态。因此，可以有很多应用场景。

与线性不同，扩展卡尔曼滤波器通常不是最佳估计器（如果测量和状态转换模型都是线性的，则它是最佳的，因为在这种情况下，扩展卡尔曼滤波器与常规滤波器相同）。此外，如果状态的初始估计是错误的，或者如果过程建模不正确，则由于其线性化，滤波器可能会很快发散。扩展卡尔曼滤波器的另一个问题是估计的协方差矩阵往往会低估真实的协方差矩阵，因此在不添加“稳定噪声”的情况下可能会在统计意义上变得不一致。更一般地，我们应该考虑非线性滤波问题的无限维性质以及简单均值和方差-协方差估计器不足以完全表示最优滤波器。还应该注意的是，即使对于非常简单的一维系统，扩展卡尔曼滤波器也可能表现不佳。在这种情况下，可以考虑其他一般的非线性滤波方法。

EKF 方法是解决 SLAM 问题的一种经典方法，其应用依赖于运动模型和观测模型的高斯噪声假设。EFK在数据融合上有很广泛的应用，相对于优化的方法，基于EKF的方法精度虽然较低但是计算效率更高。

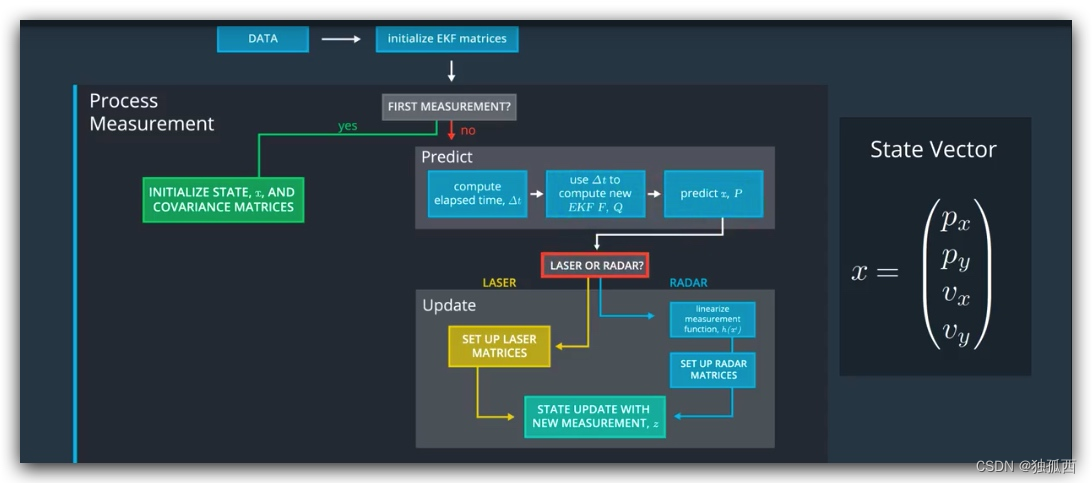
四、代码实践

参考资料[2][3]中都含有二维平面小车状态估计的仿真，非常值得看。这里放一下扩展卡尔曼滤波的C++实现，参考[4]。

kalman_filter.cpp

#include <iostream>
#include "kalman_filter.h"

#define PI 3.14159265

using namespace std;
using Eigen::MatrixXd;
using Eigen::VectorXd;

KalmanFilter::KalmanFilter() {}

KalmanFilter::~KalmanFilter() {}

void KalmanFilter::Init(VectorXd &x_in, MatrixXd &P_in, MatrixXd &F_in,
                        MatrixXd &H_in, MatrixXd &R_in, MatrixXd &Q_in) {
  x_ = x_in;
  P_ = P_in;
  F_ = F_in;
  H_ = H_in;
  R_ = R_in;
  Q_ = Q_in;
}

void KalmanFilter::Predict() {
  //Use the state using the state transition matrix
  x_ = F_ * x_;
  //Update the covariance matrix using the process noise and state transition matrix
  MatrixXd Ft = F_.transpose();
  P_ = F_ * P_ * Ft + Q_;

}

void KalmanFilter::Update(const VectorXd &z) {

  MatrixXd Ht = H_.transpose();
  MatrixXd PHt = P_ * Ht;

  VectorXd y = z - H_ * x_;
  MatrixXd S = H_ * PHt + R_;
  MatrixXd K = PHt * S.inverse();

  //Update State
  x_ = x_ + (K * y);
  //Update covariance matrix
  long x_size = x_.size();
  MatrixXd I = MatrixXd::Identity(x_size, x_size);  
  P_ = (I - K*H_) * P_;

}

void KalmanFilter::UpdateEKF(const VectorXd &z) {
  
  float px = x_(0);
  float py = x_(1);
  float vx = x_(2);
  float vy = x_(3);
  
  //Convert the predictions into polar coordinates
  float rho_p = sqrt(px*px + py*py);
  float theta_p = atan2(py,px);

  if (rho_p < 0.0001){
    cout << "Small prediction value - reassigning Rho_p to 0.0005 to avoid division by zero";
    rho_p = 0.0001;
  }
    
  float rho_dot_p = (px*vx + py*vy)/rho_p;

  VectorXd z_pred = VectorXd(3);
  z_pred << rho_p, theta_p, rho_dot_p;

  VectorXd y = z - z_pred;
  
  //Adjust the value of theta if it is outside of [-PI, PI]
  if (y(1) > PI){
    y(1) = y(1) - 2*PI;
  }

  else if (y(1) < -PI){
    y(1) = y(1) + 2*PI;
  }

  MatrixXd Ht = H_.transpose();
  MatrixXd PHt = P_ * Ht;

  MatrixXd S = H_ * PHt + R_;
  MatrixXd K = PHt * S.inverse();

  //Update State
  x_ = x_ + (K * y);
  //Update covariance matrix
  long x_size = x_.size();
  MatrixXd I = MatrixXd::Identity(x_size, x_size);  
  P_ = (I - K*H_) * P_;
}

kalman_filter.h

#ifndef KALMAN_FILTER_H_
#define KALMAN_FILTER_H_
#include "Eigen/Dense"

class KalmanFilter {
public:

  // state vector
  Eigen::VectorXd x_;

  // state covariance matrix
  Eigen::MatrixXd P_;

  // state transition matrix
  Eigen::MatrixXd F_;

  // process covariance matrix
  Eigen::MatrixXd Q_;

  // measurement matrix
  Eigen::MatrixXd H_;

  // measurement covariance matrix
  Eigen::MatrixXd R_;

  /**
   * Constructor
   */
  KalmanFilter();

  /**
   * Destructor
   */
  virtual ~KalmanFilter();

  /**
   * Init Initializes Kalman filter
   * @param x_in Initial state
   * @param P_in Initial state covariance
   * @param F_in Transition matrix
   * @param H_in Measurement matrix
   * @param R_in Measurement covariance matrix
   * @param Q_in Process covariance matrix
   */
  void Init(Eigen::VectorXd &x_in, Eigen::MatrixXd &P_in, Eigen::MatrixXd &F_in,
      Eigen::MatrixXd &H_in, Eigen::MatrixXd &R_in, Eigen::MatrixXd &Q_in);

  /**
   * Prediction Predicts the state and the state covariance
   * using the process model
   * @param delta_T Time between k and k+1 in s
   */
  void Predict();

  /**
   * Updates the state by using standard Kalman Filter equations
   * @param z The measurement at k+1
   */
  void Update(const Eigen::VectorXd &z);

  /**
   * Updates the state by using Extended Kalman Filter equations
   * @param z The measurement at k+1
   */
  void UpdateEKF(const Eigen::VectorXd &z);

};

#endif /* KALMAN_FILTER_H_ */