【教程】逻辑回归怎么做多分类

news2025/1/20 10:52:39

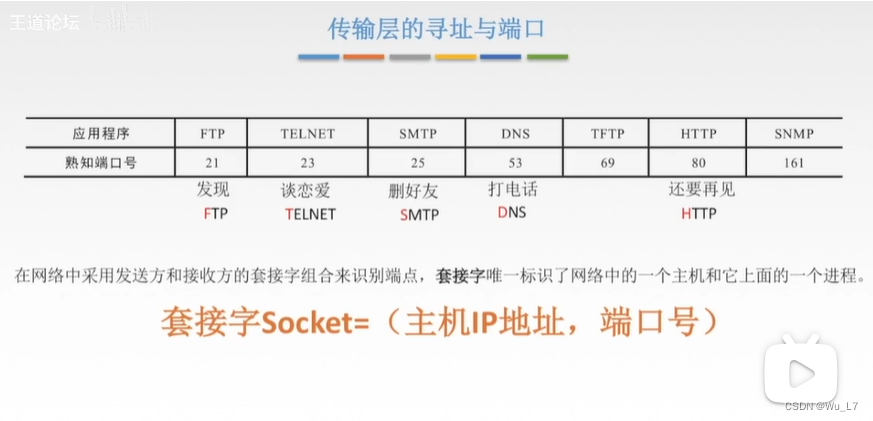
一、逻辑回归模型介绍

1.1 逻辑回归模型简介

1.2 逻辑回归二分类模型

1.3 逻辑回归多分类模型

二、如何实现逻辑回归二分类

2.1 逻辑回归二分类例子

2.2 逻辑回归二分类实现代码

三、如何实现一个逻辑回归多分类

3.1 逻辑回归多分类问题

3.1 逻辑回归多分类的代码实现

本文部分图文借鉴自《老饼讲解-机器学习》

一、逻辑回归模型介绍

1.1 逻辑回归模型简介

逻辑回归模型是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。它与多重线性回归有很多相同之处，模型形式基本相同，都具有w'x+b，其中w和b是待求参数。重线性回归直接将w'x+b作为因变量即y =w'x+b，而逻辑回归则通过sigmiod函数将w'x+b对应一个概率P，

也就是说，线性回归用于数值预测问题，而逻辑回归则用于分类问题，逻辑回归输出的是属于类别的概率。逻辑回归的意义如下图所示，用直线/超平面将不同类别的数据样本进行划分：

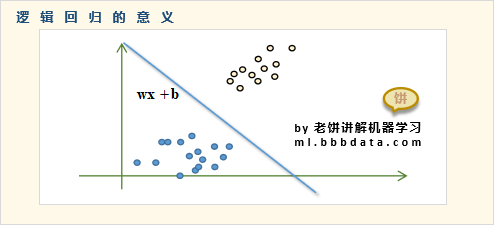
逻辑回归可以用于做二分类(即只有两个类别)，也可以做多分类(2个以上的类别)。二分类是逻辑回归的基本模型，而多分类则是二分类模型的拓展。

1.2 逻辑回归二分类模型

逻辑回归的二分类模型如下：

它的损失函数为最大似然损失函数：

模型中的参数W就是通过求解损失函数，令损失函数取最小值，从而求得W的最优解。模型的求解一般使用梯度下降法。

1.3 逻辑回归多分类模型

逻辑回归多分类模型是二分类模型的拓展。主要有softmax回归和OVR两种拓展方法,其中，OVR是基于二分类模型的一种通用拓展方法。两种方法的原理如下：

softmax回归：softmax回归是逻辑回归在多分类问题上的推广，通过修改逻辑回归的损失函数，将逻辑回归变为softmax回归。softmax回归会有相同于类别数的输出，输出的值为对于样本属于各个类别的概率，最后对于样本进行预测的类型为概率值最高的那个类别。
OVR(基于二分类的逻辑回归)：根据每个类别都建立一个二分类器，本类别的样本标签定义为0，其它分类样本标签定义为1，则有多少个类别就构造多少个逻辑回归分类器。这种方法实际上是将多分类问题划分为多个二分类问题来解决。
上述两种方法都是常用的逻辑回归多分类方法，无论采用哪种方法，逻辑回归多分类模型都需要根据具体问题和数据集进行调整和优化，以获得更好的分类性能。

当为Softmax回归时，逻辑回归多分类的模型表达式如下：

当为OVR模型时，逻辑回归多分类的模型表达式如下

$P_k(x)=\textbf{sigmoid}(WX)$

其中， $P_k$ 代表属于k类的概率

二、如何实现逻辑回归二分类

2.1 逻辑回归二分类例子

在python中，可以使用sklearn的LogisticRegression实现一个逻辑回归的，例子如下

具体数据如下：

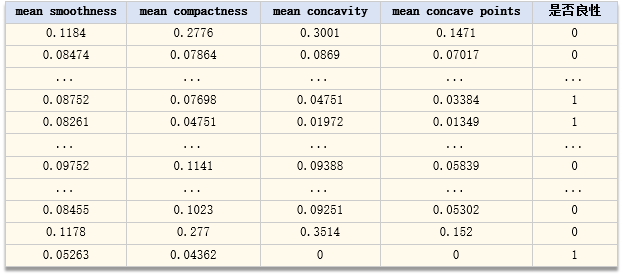
特征：平均平滑度、平均紧凑度、平均凹面、平均凹点，类别：0-恶性、1-良性
即以sk-learn中的breast_cancer的数据，breast_cancer原数据中有30个特征，为方便讲解，我们这里只选4个。下面展示调用sklearn训练一个逻辑回归的DEMO代码

2.2 逻辑回归二分类实现代码

代码简介：
1. 数据归一化（用sklearn的逻辑回归一般要作数据归一化）
2. 用归一化数据训练逻辑回归模型
3. 用训练好的逻辑回归模型预测

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
import numpy as np

#----数据加载------
data = load_breast_cancer()
X    = data.data[:,4:8]  #这里我们只选择4个变量进行建模
y    = data.target
#----数据归一化------
xmin=X.min(axis=0)
xmax=X.max(axis=0)
X_norm=(X-xmin)/(xmax-xmin)

#-----训练模型--------------------
clf = LogisticRegression(random_state=0)            
clf.fit(X_norm,y)

#------模型预测-------------------------------
pred_y      = clf.predict(X_norm)              # 预测类别
pred_prob_y    = clf.predict_proba(X_norm)[:,1]   # 预测属于1类的概率

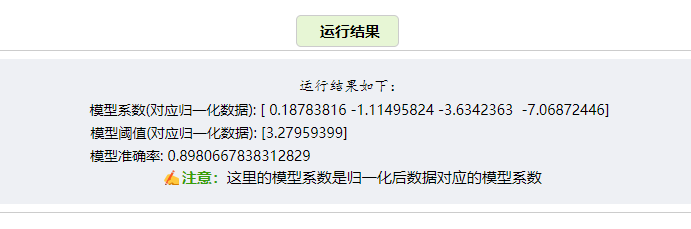
print( "模型系数(对应归一化数据):",clf.coef_[0])
print( "模型阈值(对应归一化数据):",clf.intercept_)
print( "模型准确率:",(pred_y== y).sum()/len(y))

运行结果如下：

三、如何实现一个逻辑回归多分类

3.1 逻辑回归多分类问题

下面是一个简单的多分类问题
问题
现已采集150组鸢尾花数据，
包括鸢尾花的四个特征与鸢尾花的类别
我们希望通过采集的数据，训练一个决策树模型
之后应用该模型，可以根据鸢尾花的四个特征去预测它的类别
数据
数据如下（即sk-learn中的iris数据）：

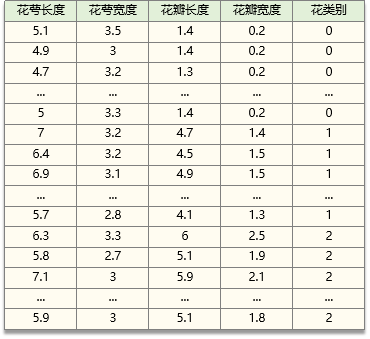
花萼长度 sepal length (cm) 、花萼宽度 sepal width (cm)
花瓣长度 petal length (cm) 、花瓣宽度 petal width (cm)
山鸢尾：0,杂色鸢尾：1,弗吉尼亚鸢尾：2

3.1 逻辑回归多分类的代码实现

用多类别逻辑回归解决该问题的具体思路如下
1. 数据归一化（用sklearn的逻辑回归一般要作数据归一化）
2. 用归一化数据训练逻辑回归模型
3. 用训练好的逻辑回归模型预测
4. 模型参数提取

# -*- coding: utf-8 -*-
"""
sklearn逻辑回归多分类例子(带模型公式提取)
"""
from sklearn.linear_model import LogisticRegression
import numpy as np
from sklearn.datasets import load_iris
#----数据加载------

iris = load_iris()    
X    = iris.data
y    = iris.target
#----数据归一化------
xmin   = X.min(axis=0)
xmax   = X.max(axis=0)
X_norm = (X-xmin)/(xmax-xmin)

#-----训练模型--------------------
clf = LogisticRegression(random_state=0,multi_class='multinomial')            
clf.fit(X_norm,y)

#------模型预测-------------------------------
pred_y      = clf.predict(X_norm)
pred_prob_y    = clf.predict_proba(X_norm) 

#------------提取系数w与阈值b-----------------------
w_norm = clf.coef_                             # 模型系数(对应归一化数据)
b_norm = clf.intercept_                           # 模型阈值(对应归一化数据)
w    = w_norm/(xmax-xmin)                       # 模型系数(对应原始数据)
b    = b_norm -  (w_norm/(xmax - xmin)).dot(xmin)      # 模型阈值(对应原始数据)
# ------------用公式预测------------------------------
wxb = X.dot(w.T)+ b
wxb = wxb - wxb.sum(axis=1).reshape((-1, 1)) # 由于担心数值过大会溢出，对wxb作调整
self_prob_y = np.exp(wxb)/np.exp(wxb).sum(axis=1).reshape((-1, 1))
self_pred_y = self_prob_y.argmax(axis=1)


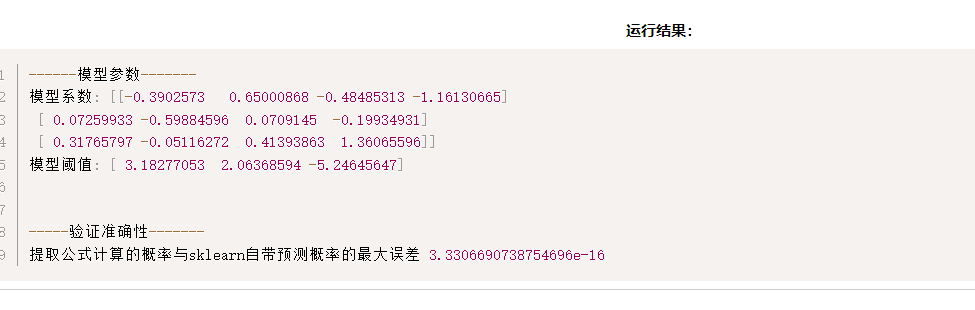
#------------打印信息--------------------------
print("\n------模型参数-------")     
print( "模型系数:",w)
print( "模型阈值:",b)
print("\n-----验证准确性-------")  
print("提取公式计算的概率与sklearn自带预测概率的最大误差", abs(pred_prob_y-self_prob_y).max())

运行结果如下：