最长递增子序列

暴力解法:
思路:使用动态规划的思想,判断当前元素之前的所有元素,如果比当前元素小,则修改当前元素的最长递增子序列(需判断是否需要修改)。
时间复杂度:O(n^2)
import java.util.Arrays;
class Solution {
public int lengthOfLIS(int[] nums) {
int dp[] = new int[nums.length];
Arrays.fill(dp, 1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
Arrays.sort(dp);
return dp[nums.length - 1];
}
}题目所给nums长度比较小,使用暴力解法可以ac。
俄罗斯套娃问题
此题也是一道求最长上升子序列的问题,不过值范围较大,暴力解法会TLE。
那么需要我们对最长上升子序列问题进行优化。
此处以最长上升子序列问题为例进行优化。
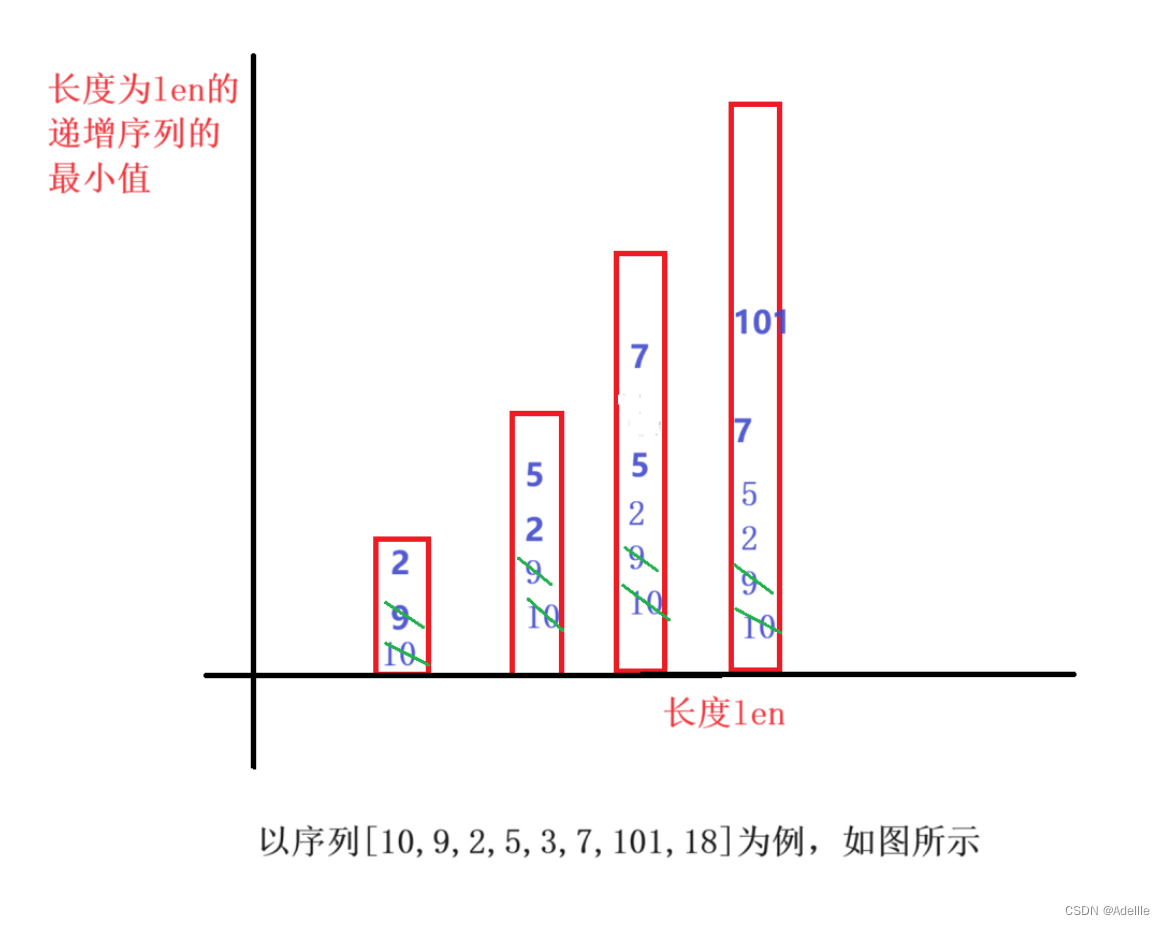
思路:我们的目的是寻找最长递增子序列,通过观察可以发现在相同长度下,两个元素较小的那个元素更有扩展为更长的子序列的潜力。
例如[3,1,2,4] ,在子序列长度同为1的情况下,如果选择了3,那么后面比3大的元素一定比1大,所以选1比选3有更大的机会生成一个最长递增子序列。
有了上面的铺垫,我们可以创建一个数组,在每个长度范围内都会存在一个大于子序列所有元素的最大值,用其来记录长度为len的递增子序列的最大值。遍历数组,每次替换掉长度序列里的刚好大于当前元素的最大值。最后返回最长的子序列长度即可。
(建议可以自己模拟遍历一遍)
这里是基于动态规划的思想,但是没有用到动态规划,使用了二分搜索优化。
时间复杂度:O(nlog(n))
class Solution {
public static int lengthOfLIS(int[] nums) {
int len = 0;//记录p的长度
int p[] = new int[2510];
for (int i = 0; i < nums.length; i++) {
int l = 0, r = len;
while (l < r) {
int mid = (l + r + 1) / 2;
if (p[mid] < nums[i]) {
l = mid;
} else {
r = mid - 1;
}
}
p[r + 1] = nums[i];
len = Math.max(len, r + 1);
}
return len;
}
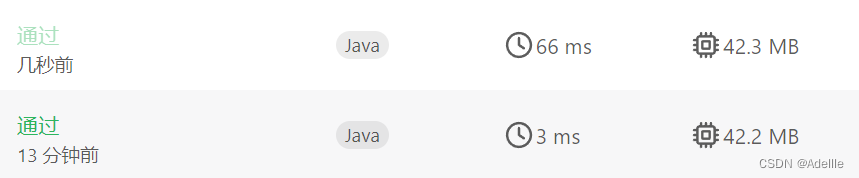
}两种时间复杂度对比





![[node] Node.js的Web 模块](https://img-blog.csdnimg.cn/999f27a1616742569128568e8d1f3b4a.png)