A. Hossam and Combinatorics
题目链接:Problem - A - Codeforces

样例输入:
2
5
6 2 3 8 1
6
7 2 8 3 2 10
样例输出:
2
4
题意:给定一个有n个元素的数组,然后让我们求出有多少对(i,j)满足|a[i]-a[j]|=max|a[p]-q[q]|(1<=p,q<=n).
分析:容易发现差的绝对值的最大值一定是数组中的最大值减去最小值得到的,所以我们可以求出来最大值的出现次数cntx和最小值的出现次数cntn,如果最大值等于最小值那么就代表所有的数都是相同的,那么就任意选两个就行,答案就是C(cntn,2)*2,别忘记是带有顺序的,即点对(i,j)和点对(j,i)被看作是不同的点对。如果最大值不等于最小值,那么就随便选一个最大值和一个最小值即可,答案就是cntx*cntn*2.
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
int main()
{
int T;
cin>>T;
while(T--)
{
int n;
scanf("%d",&n);
int mn=1e5+1,mx=0,cntn=0,cntx=0;
for(int i=1;i<=n;i++)
{
int t;
scanf("%d",&t);
if(t>mx)
{
mx=t;
cntx=1;
}
else if(t==mx) cntx++;
if(t<mn)
{
mn=t;
cntn=1;
}
else if(t==mn) cntn++;
}
if(mx!=mn) printf("%lld\n",1ll*cntn*cntx*2);
else printf("%lld\n",1ll*cntn*(cntn-1));
}
return 0;
}B. Hossam and Friends
题目链接:Problem - B - Codeforces

样例输入:
2
3 2
1 3
2 3
4 2
1 2
2 3
样例输出:
4
5
题意:一开始给定一个n和m,n代表人数,编号从1~n,m代表关系数,每对关系给定两个编号x和y,代表编号为x的人和编号为y的人不认识,现在按照编号顺序从左到右站成一排,问有多少个区间[l,r]满足区间内的人都是互相认识的。
分析:我们不妨按照以某个点为左区间的满足题意的区间个数的方法进行统计,用r[i]记录与编号为i的人互不认识的人的编号的最小值,那么对于每一个i所能到达的区间右边界的最大值就是min(r[i~n]),那么以编号i为左边界的满足题意的区间个数就是min(r[i~n])-i,而min(r[i~n])我们可以用ST表处理一下就行。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e5+10;
long long r[N],f[N][32];
long long find(int l,int r)
{
int t=(int)log2(r-l+1);
return min(f[l][t],f[r-(1<<t)+1][t]);
}
int main()
{
int T;
cin>>T;
while(T--)
{
long long n,m;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++) r[i]=n+1;
for(int i=1;i<=m;i++)
{
long long x,y;
scanf("%lld%lld",&x,&y);
long long mn=min(x,y),mx=max(x,y);
r[mn]=min(r[mn],mx);
}
for(int i=1;i<=n;i++)
f[i][0]=r[i];
for(int i=1;i<=30;i++)
for(int l=1;l-1+(1<<i)<=n;l++)
f[l][i]=min(f[l][i-1],f[l+(1<<(i-1))][i-1]);
long long ans=0;
for(int i=1;i<=n;i++)
ans+=find(i,n)-i;
printf("%lld\n",ans);
}
return 0;
}C. Hossam and Trainees
题目链接:Problem - C - Codeforces

样例输入:
2
3
32 48 7
3
14 5 9
样例输出:
YES
NO
题意:给你n个数,问这n个数中是否存在不互质的两个数,存在输出YES,否则输出NO
分析:欧拉筛预处理一下1e5以内的素数,然后直接用map记录含有每个素数因子的出现次数,如果出现次数大于等于2则说明有多个数含有相同的因子,则说明存在不互质的数对,否则就说明不存在。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e5+10;
long long prime[N],tt;
bool vis[N];
void init()
{
for(int i=2;i<N;i++)
{
if(!vis[i]) prime[++tt]=i;
for(int j=1;j<=tt&&i*prime[j]<N;j++)
{
vis[i*prime[j]]=true;
if(i%prime[j]==0) break;
}
}
}
int main()
{
int T;
cin>>T;
init();
while(T--)
{
long long n;
scanf("%lld",&n);
map<long long,int>mp;
bool flag=false;
for(int i=1;i<=n;i++)
{
long long t;
scanf("%lld",&t);
if(flag) continue;
for(int j=1;prime[j]*prime[j]<=t;j++)
if(t%prime[j]==0)
{
if(mp[prime[j]])
{
flag=true;
break;
}
while(t%prime[j]==0) t/=prime[j];
mp[prime[j]]=1;
}
if(t!=1)
{
if(mp[t])
flag=true;
mp[t]=1;
}
}
if(flag) puts("YES");
else puts("NO");
}
return 0;
}D. Hossam and (sub-)palindromic tree
题目链接:Problem - D - Codeforces

样例输入:
2
5
abaca
1 2
1 3
3 4
4 5
9
caabadedb
1 2
2 3
2 4
1 5
5 6
5 7
5 8
8 9
样例输出:
3
5
题意:给定一棵由26个英文字符组成的字典树,问由两个节点之间的路径所代表的字符串中的最长回文子序列的长度。
分析:先来探讨一个基本的问题:给定一个长度为n的字符串,如何求这个字符串中的最长回文子序列的长度?
这是一个比较经典的问题,可以用区间DP来求解,设f[i][j]表示从第i个字符到第j个字符中的最长回文子序列的长度,那么分下面两种情况:
(1)第i个字符和第j个字符是相同的,那么就有f[i][j]=2+f[i+1][j-1]
(2)第i个字符和第j个字符是不同的,那么就有f[i][j]=max(f[i+1][j],f[i][j-1])
按照这个方法,我们就能在O(n^2)的复杂度内将这个问题解决
而下面这个问题其实也是类似的,只不过是在树上而已。
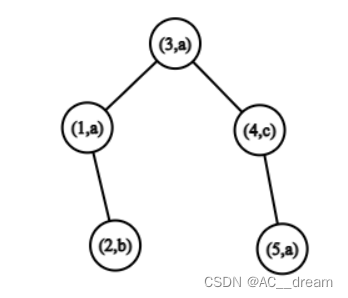
拿这个图来说,假如我们要求解节点1和节点5之间的最长回文子序列的长度,那么我们首先要看一下节点1和节点5的字符是否相同,发现都是a,那么结果就变为2+节点3和节点4之间的最长回文子序列的长度。这个过程我们可以用记忆化搜索,如果搜索到了已知答案我们就可以直接返回,否则就继续搜索,因为每个区间只会被更新一次,所以总的复杂度就是O(n^2)。按照刚才的方法去搜索可以发现我们是要用到每个节点的父节点的,所以我们可以直接dfs求出每个节点的父节点。讲解题目一开始所引入的例子就是一个已知字符串序列的最长回文子序列的求法,那么在搜索过程中我们可以用栈来记录从根节点到该节点的路径,那么我们直接对这个问题进行求解就可以求出来任意一个节点到其任意一个父节点之间的最长回文子序列的长度,那么至于不存在祖先关系两个节点之间的最长回文子序列的长度我们就可以按照刚才所讲述的关系一步一步向其祖先节点搜索,直至搜索到一方是另一方的祖先节点,那么我们就可以直接返回答案了。整个过程采用记忆化搜索,总体复杂度就是O(n^2),细节比较多,见代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=4e5+10;
int h[N],e[N],ne[N],idx,fa[N];
int f[2003][2003];//f[i][j]表示节点i到节点j的最长回文序列长度
char s[N];
int st[N],tt;
void add(int x,int y)
{
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
void dfs(int x,int ffa)
{
fa[x]=ffa;
f[x][x]=1;
st[++tt]=x;
for(int i=tt-2;i>=1;i--)
if(s[x]==s[st[i]]) f[x][st[i]]=f[st[i]][x]=2+f[st[i+1]][fa[x]];
else f[x][st[i]]=f[st[i]][x]=max(f[x][st[i+1]],f[fa[x]][st[i]]);
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(j==ffa) continue;
if(s[j]==s[x]) f[j][x]=f[x][j]=2;
else f[j][x]=f[x][j]=1;
dfs(j,x);
}
--tt;
}
int fun(int x,int y)//求节点x与节点y之间的最长回文子序列长度
{
if(f[x][y]!=-1) return f[x][y];
else if(s[x]==s[y]) return f[x][y]=fun(fa[x],fa[y])+2;
else return f[x][y]=max(fun(fa[x],y),fun(x,fa[y]));
}
int main()
{
int T;
cin>>T;
while(T--)
{
int n;
scanf("%d%s",&n,s+1);
int u,v;
for(int i=1;i<=n;i++) h[i]=-1;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=-1;
idx=0;
for(int i=1;i<n;i++)
{
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
dfs(1,-1);
int ans=0;
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++)
ans=max(ans,fun(i,j));
printf("%d\n",ans);
}
return 0;
}