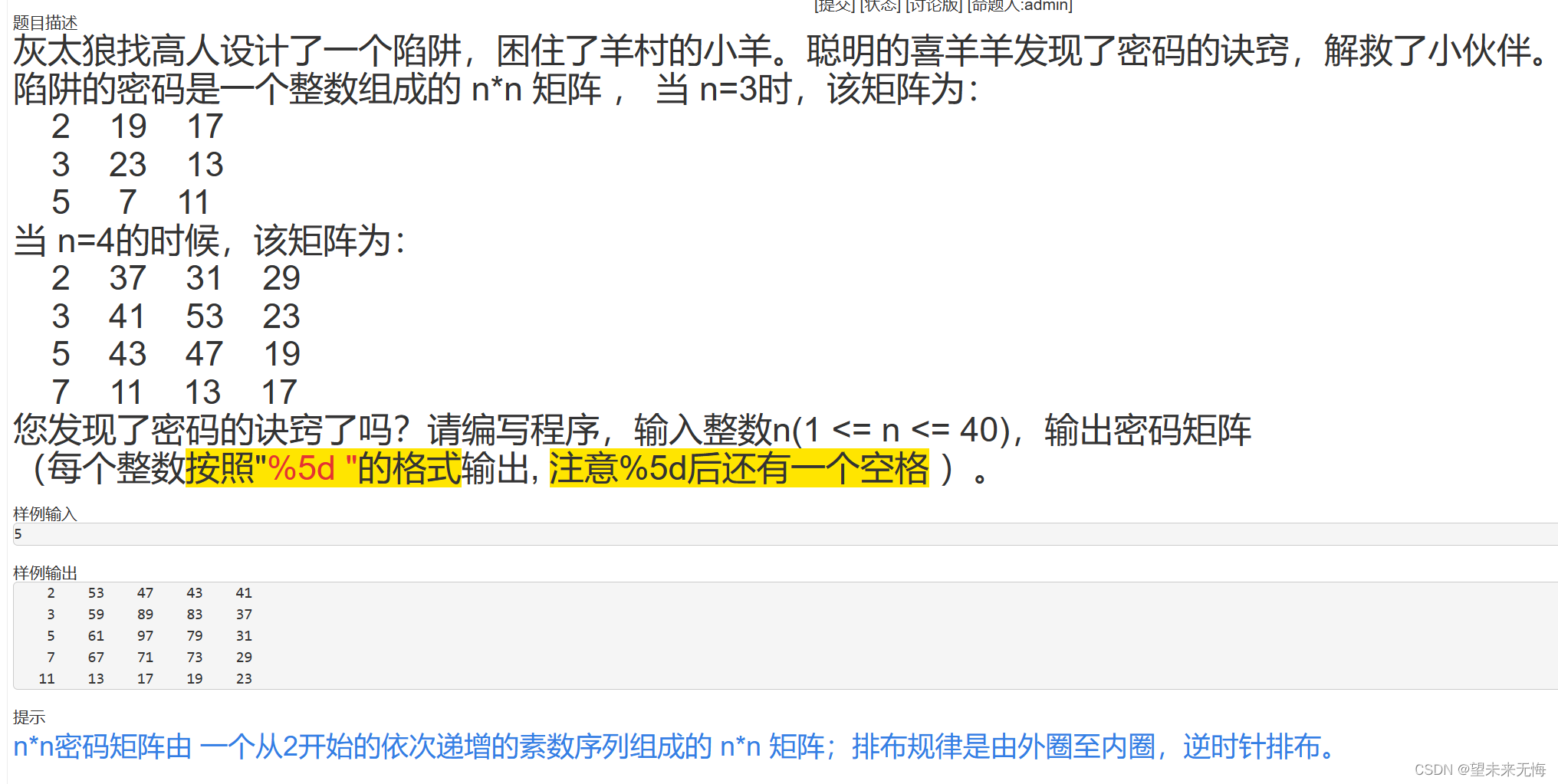
分析：本题主要使用的是素数进行输出，然后难点是如何按照题目要求格式输出。

思路：

第一：我们可以先让素数存给一个一维数组，至于存多少个素数，是矩阵n*n个，控制数量用计数器count即可，将所需要足够的素数存到一维数组后，就该考虑如何让这些元素按照题目格式。

第二：易知输出格式是二维的，因此要动用二维数组，创建一个新的二维数组，想办法将一维数组的元素存到二维数组中（按照题目格式）

第三：数组最重要的特点就是下标，因此我们要利用好下标，下面以4*4矩阵为例，画图分析

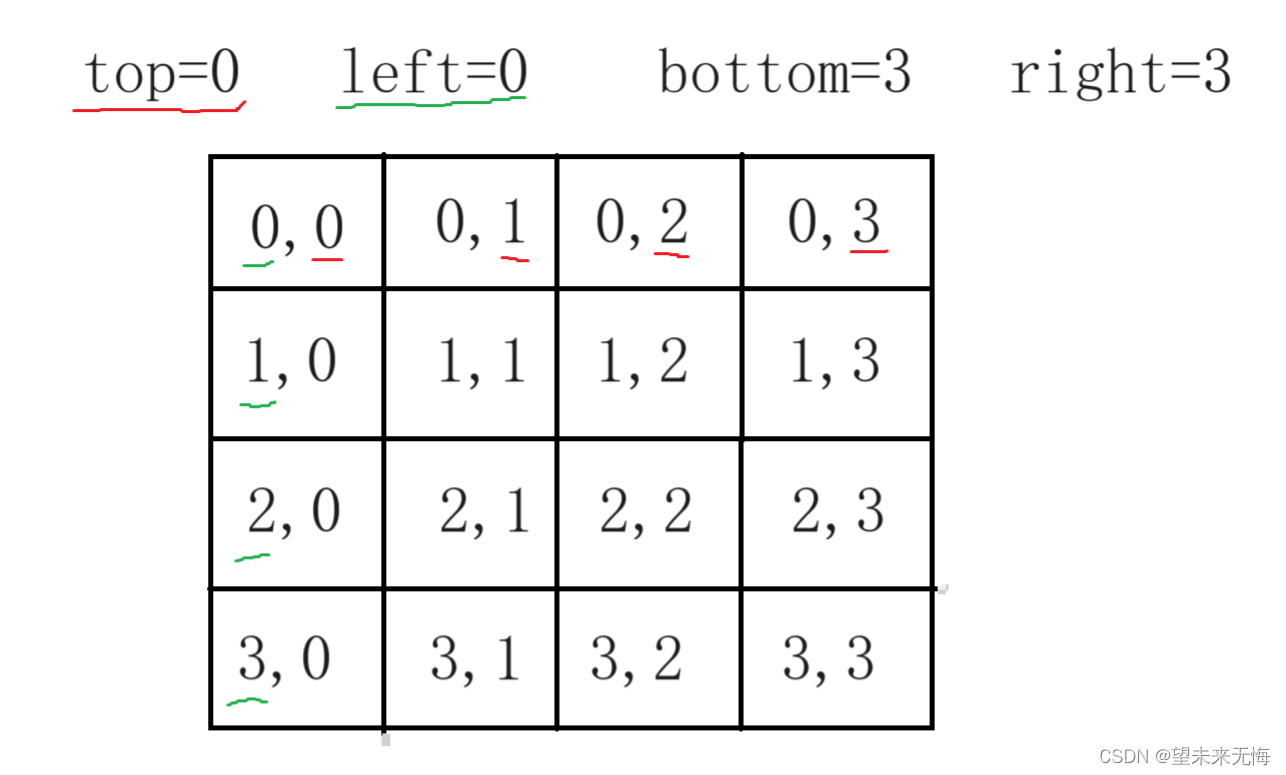
以从上到下，从左到右的顺序，top和left作为初始值0，bottom和right作为边界值3

按照逆时针顺序

第一步下标：行不变列增加，即（0，0）到（3，0）；

第二步下标：列不变行增加，即（3，0）到（3，3）；

第三步下标：行不变列减少，即（3，3）到（0，3）；

第四步下标：列不变行减少，即（0，3）到（0，1）；

于是最外围的解决完后发现内圈还是矩阵，于是再次循环……

第四：将一维数组中所有的素数都存给二维数组后，就打印该二维数组

答案：

#include <stdio.h>
#include <math.h>

int is_prime(int n)  // 判断是否为素数
{
    if (n <= 1)   //2是最小的素数，所以比2小的都不是素数
    {
        return 0;  //为假
    }
    int sqr = sqrt(n);   
    for (int i = 2; i <= sqr; i++)    //优化算法
    {
        if (n % i == 0)   //有其他因子
        {
            return 0;   //为假
        }
    }
    return 1;   //否则是素数，为真
}

int main() 
{
    int n = 0;
    scanf("%d", &n);
    int primes[1600] = { 0 }; // 存储素数序列的一维数组
    int count = 0; // 计数器计算已有素数个数
    int num = 2; // 从2开始判断素数
    while (count < n * n)  // 存n*n个的素数
    {
        if (is_prime(num)) 
        {
            primes[count++] = num;
        }
        num++;
    }
    int arr[40][40]; // 存储密码矩阵的二维数组
    int left = 0, right = n - 1, top = 0, bottom = n - 1; // 四个边界
    int index = 0; // 素数序列下标 
    while (left <= right && top <= bottom)   //判断是否还有内圈
    { 
        for (int i = top; i <= bottom; i++)    //第一步
        {
            arr[i][left] = primes[index++];
        }
        for (int i = left + 1; i <= right; i++)   //第二步
        {
            arr[right][i] = primes[index++];
        }
        for (int i = bottom - 1; i >= top; i--)    //第三步
        {
                arr[i][right] = primes[index++];
        }
        for (int i = right - 1; i > left; i--)    //第四步
        {
                arr[top][i] = primes[index++];
        }
        left++;    //初始值加1
        right--;   //边界值减1
        top++;     //初始值加1
        bottom--;  //边界值减1
    }
    for (int i = 0; i < n; i++)    //输出密码矩阵
    {
        for (int j = 0; j < n; j++)
        {
            printf("%5d ", arr[i][j]);
        }
        printf("\n");
    }
    return 0;
}