数据结构初阶之二叉树的详细解析

个人主页：点我进入主页

专栏分类：C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶

C语言刷题数据结构初阶 Linux

欢迎大家点赞，评论，收藏。

一起努力,共赴大厂。

1.前言

2.二叉树各个功能代码实现

2.1二叉树结构体

2.2二叉树的前序遍历

2.3中序遍历

2.4后序遍历

2.5计算二叉树节点个数

2.6计算二叉树叶子节点的个数

2.7计算二叉树的深度

2.8计算第k层的节点个数

2.9层序遍历

2.10层序遍历变式

2.11判断是否为完全二叉树

2.12二叉树内存释放

2.13树的创建

3.二叉树的性质

4.总结

1.前言

我在前面写过关于顺序表，栈，队列，堆的存储结构，现在我们还有一种一对多的存储结构树，在堆的博客中我写过一些树的概念，树的增删查改在我们的应用中并不实用，其中有用的是查找树，但是查找树的实现我们还没有能力去实现，树的实现可以用顺序表实现也可以用链表去实现，这次我们用链式二叉树去实现，利用顺序表实现可以看堆的内容。在这篇文章中我主要给大家带来关于二叉树的创建，树的一些性质，树的前序中序后序层序遍历，求树的节点个数，叶子节点个数，树的深度，第k层节点的个数，判断是不是完全二叉树，在这些中大部分需要用递归，我会给搭建展示部分功能的递归展开图来帮助大家理解，在学习这写内容中我建议大家可以会回忆一下递归的内容，是不是看到递归就觉得畏惧吗？其实我们只需要多去感受一下其中的思路与思想，不用过多的去畏惧递归，接下来就让我们看看其中是如何用递归去实现吧。

2.二叉树各个功能代码实现

2.1二叉树结构体

typedef struct BiTreeNode {
	int val;
	struct BiTreeNode* left, * right;
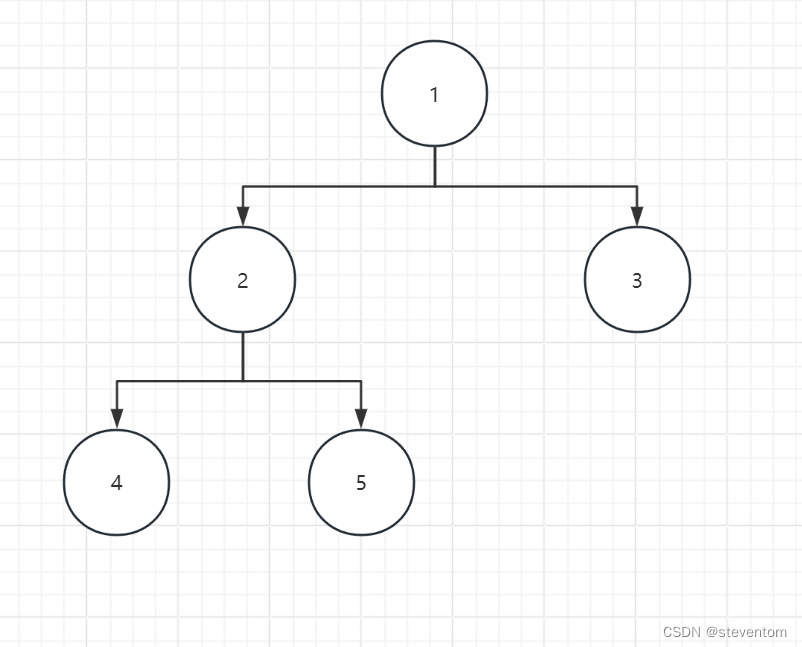
}BTNode;

结构体的内容包括结构体的内容，指向二叉树的左孩子的指针，指向二叉树的右孩子的指针。我给大家来看一下二叉树的大概的模型

2.2二叉树的前序遍历

void PrevorderBTNode(BTNode* root)
{
	if (root == NULL)
		return;
	printf("%d ", root->val);
	PrevorderBTNode(root->left);
	PrevorderBTNode(root->right);
}

例如我们利用上面的二叉树进行模拟

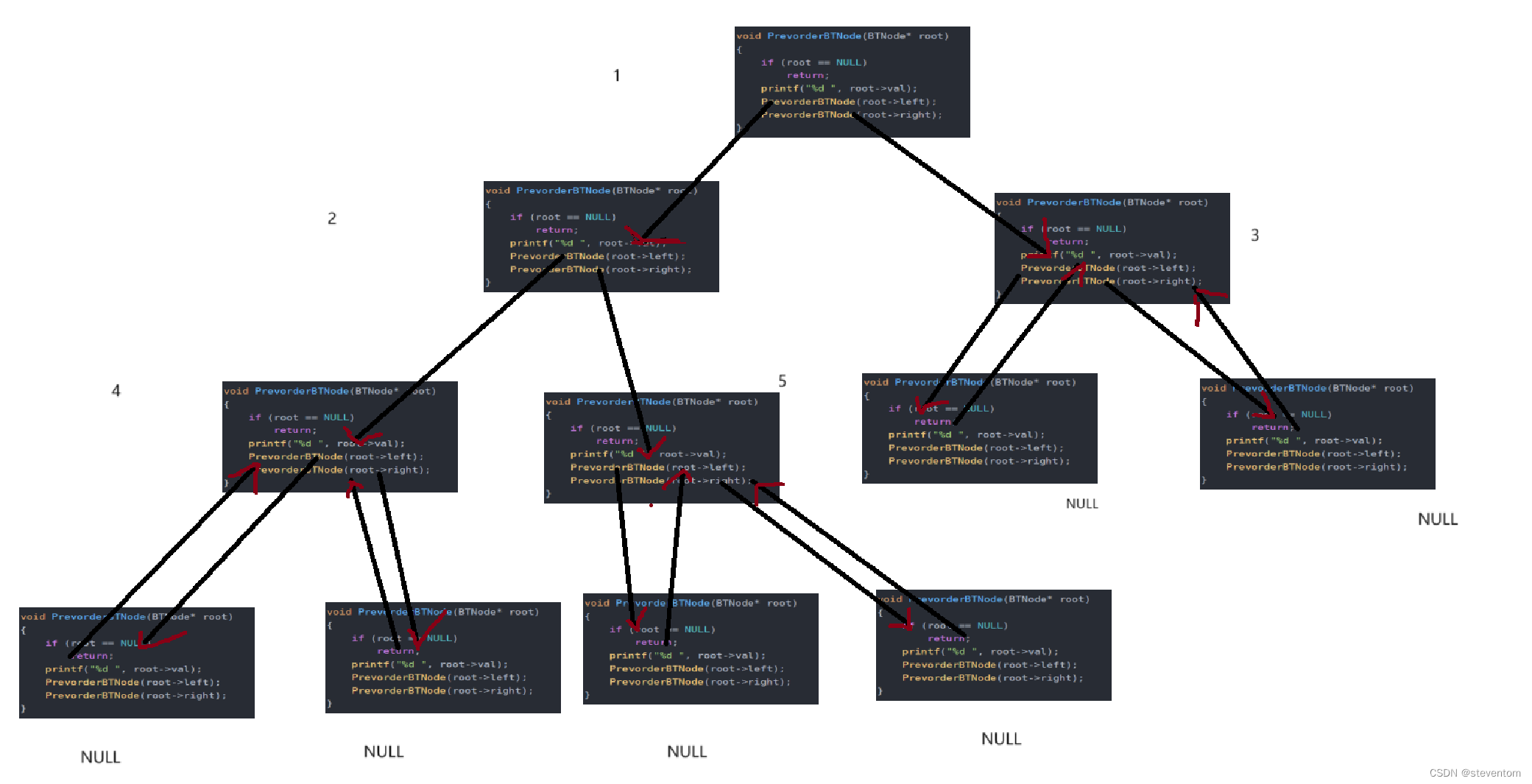
我们可以根据代码展开图进行一步步实现代码实现的过程，最好我们自己去画一画代码展开图这样对于我们去了解递归会有非常好的作用。

2.3中序遍历

void InorderBTNode(BTNode* root)
{
	if (root == NULL)
		return;
	InorderBTNode(root->left);
	printf("%d ", root->val);
	InorderBTNode(root->right);
}

我们的代码展开图如下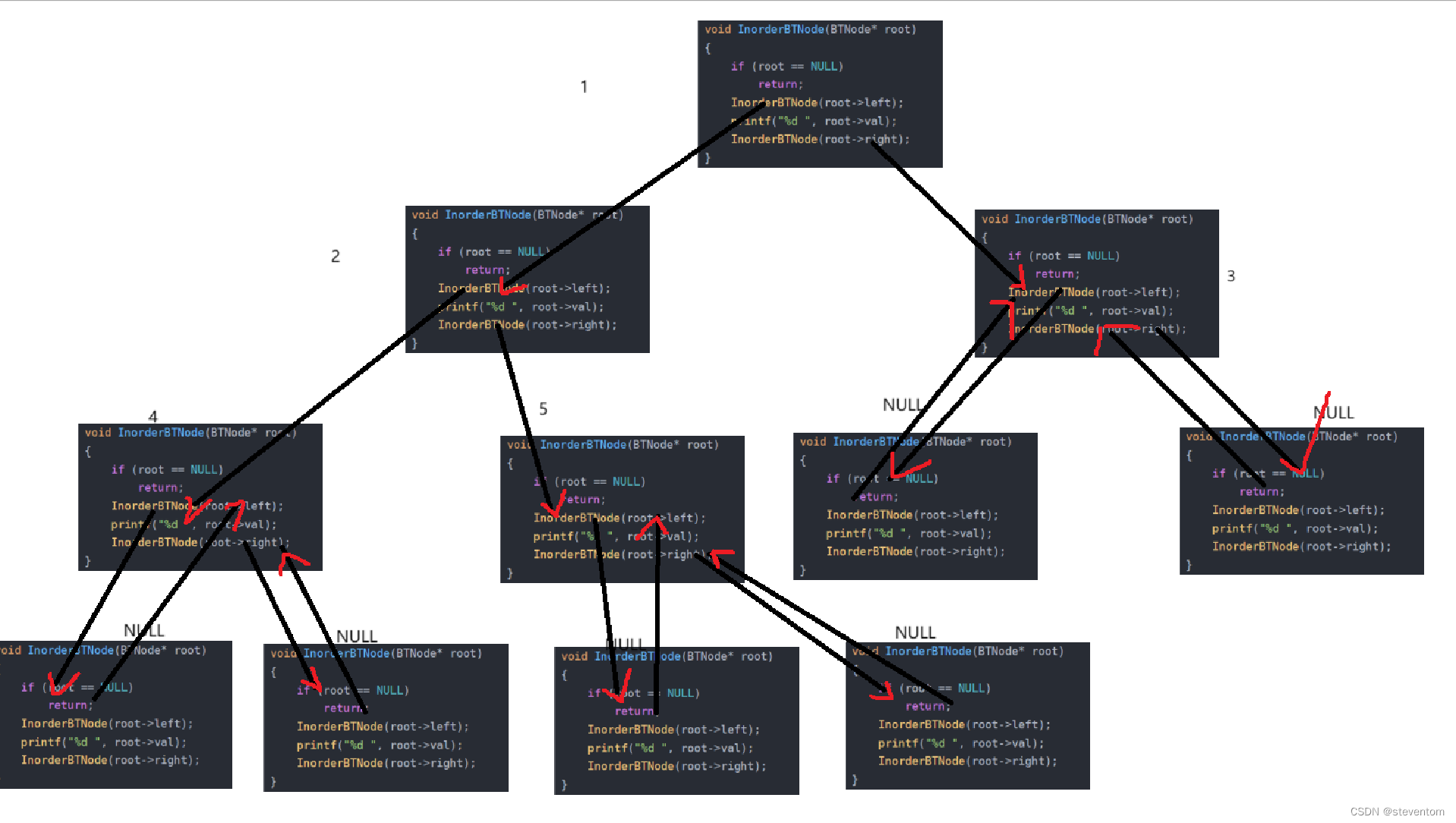

我们可以看到我们的中序遍历代码和前序遍历代码大致相同，相差的只是代码的顺序，我们可以将大部分二叉树的递归可以表示为根节点，左孩子右孩子，左子树右子树和根节点，左孩子右孩子这两种，这非常有用是一种分治的思想。

2.4后序遍历

void PostorderBTNode(BTNode* root)
{
	if (root == NULL)
		return;
	PostorderBTNode(root->left);
	PostorderBTNode(root->right);
	printf("%d ", root->val);
}

在这里我们不给代码展开图了，大家可以自己去画一画代码展开图。

2.5计算二叉树节点个数

int BTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return BTreeSize(root->left) + BTreeSize(root->right) + 1;
}

我们想到二叉树的递归内容可以表示为根节点，左孩子右孩子，左子树右子树或根节点，左孩子右孩子，我们可以看成根节点，左子树右子树，当根节点为空时我们返回0，我们分为左子树和右子树所以我们返回BTreeSize(root->left) + BTreeSize(root->right) + 1进行递归，我们的递归展开图可以画为

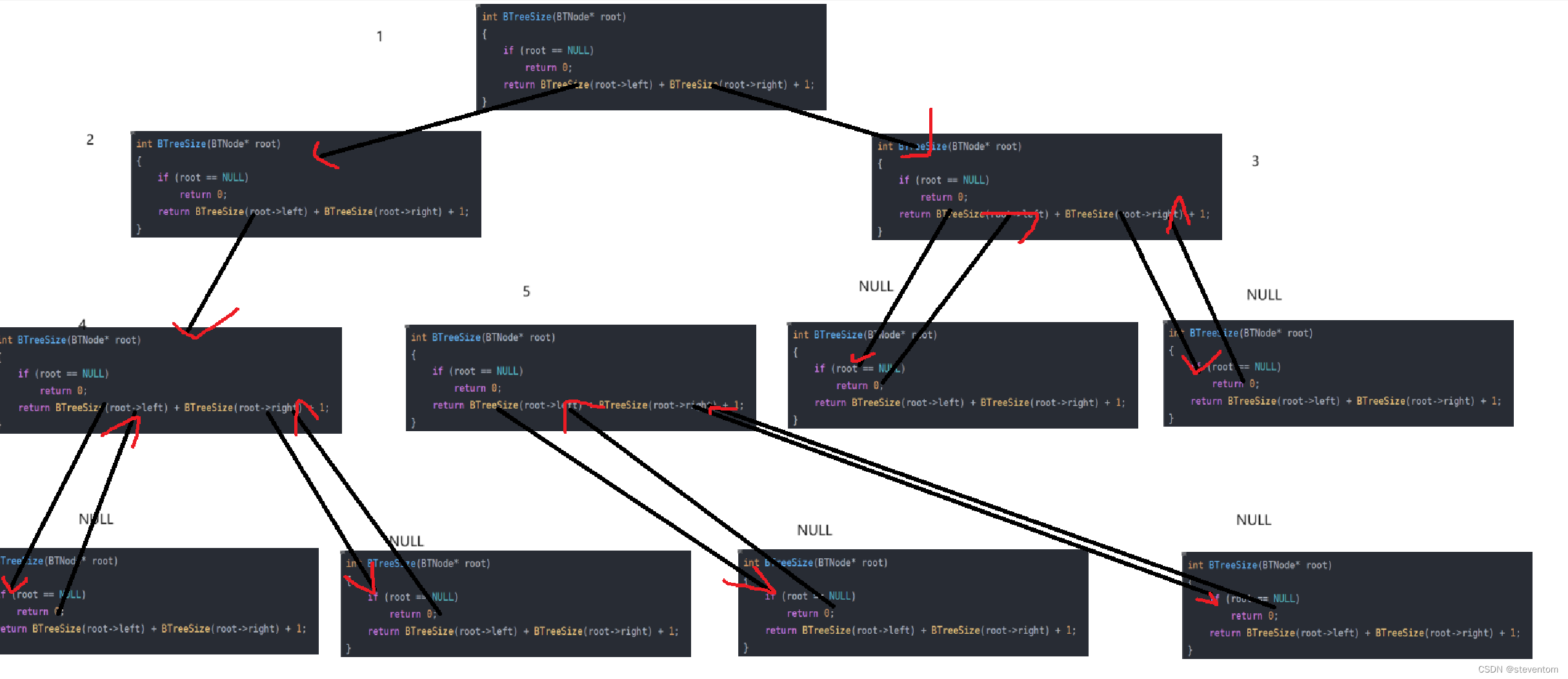
2.6计算二叉树叶子节点的个数

我们可以根据根据根节点，左子树右子树进行分治，当我们的根节点为空时返回0，当左孩子和右孩子为空是叶子节点返回1，对于左子树和右子树我们进行递归。

int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}

递归展开图和上面的相似，大家可以自己去画一画。

2.7计算二叉树的深度

我们可以根据根据根节点，左子树右子树进行分治，当根节点为空时返回0，然后进行递归。

int BTreeDeap(BTNode* root)
{
	if (root == NULL)
		return 0;
	return (int)fmax(BTreeDeap(root->left), BTreeDeap(root->right)) + 1;
}

2.8计算第k层的节点个数

int BTreeLeafkSize(BTNode* root,int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BTreeLeafkSize(root->left, k-1) + BTreeLeafkSize(root->right, k-1);
}

当我们的根节点是空时我们返回0，当我们的k变成1时我们返回1，根据左子树右子树进行分治每次都让k-1。

2.9层序遍历

void Levelorder(BTNode* root)
{
	Queue queue;
	QueueInit(&queue);
	if (root)
	{
		QueuePush(&queue, root);
	}
	while (!QueueEmpty(&queue))
	{
		BTNode* prev = top(&queue) ;
		QueuePop(&queue);
		if (prev->left)
			QueuePush(&queue, prev->left);
		if (prev->right)
			QueuePush(&queue, prev->right);
		printf("%d ", prev->val);
	}
}

在层序遍历中我们利用队列进行存储，先将非空的根节点进行插入，进行循环队列不为空进行循环，利用一个二叉树的指针指向队头的元素（队列里的元素存的是二叉树的节点时结构体的指针所以我们可以用二叉树的指针进行指向），然后出队，入指针的非空左孩子右孩子，每次打印指针对应的值。

2.10层序遍历变式

如果我们想每层打印时打印完每次会输出一个换行，这时候我们应该如何作呢？我们首先想到的是再搞一个队列，存放第一个队列元素是第几层，但是我们c语言去实现队列是非常麻烦的，连结构体都需要我们去重新设定，那我们应该如何去做呢？在我们的层序遍历中你有没有注意到我们的队列中总是存在全部的一层元素或者一层与下一层的元素这两种情况，什么时候会出现只有一层的元素呢？那就是上一层全部出队了，这便是我们的突破点，当我们将非空根节点入队后我们引入一个变量存放队中的元素的个数然后进入循环，此时这个变量就是一层元素的个数，我们每次出一个元素就让这个变量减1，这也就是我们的循环条件，循环结束后我们重新计算这个变量的值，这时候队中还是只有一层全部的节点，此时变量的值就是队中元素的个数。

2.11判断是否为完全二叉树

bool BinaryTreeComplete(BTNode* root)
{
	Queue queue;
	QueueInit(&queue);
	if (root)
		QueuePush(&queue, root);
	while (top(&queue))
	{
		BiTreeNode* front = top(&queue);
		QueuePop(&queue);
		QueuePush(&queue, front->left);
		QueuePush(&queue, front->right);
	}
	return QueueEmpty(&queue);

}

首先我们需要了解完全二叉树的性质，他和满二叉树类似，但是序号必须和满二叉树相同，这时候我们采用层序遍历的方式进行判断，我们将非空根节点入队，判断条件是队头元素不是空，每个节点入队当我们遇到空节点时我们判断队是不是都是空节点，如果是就是完全二叉树，为什么这样可以呢？当我们入队后一旦想出某一层时这一层的全部节点就会入队，然后进行判断就可以了。

2.12二叉树内存释放

二叉树内存前序中序后序都可以实现，但是我们如何做才能让这个操作根号的实现呢？我们想类似于前中后序遍历的样子进行，这时候你会发现，利用前序和中序遍历会提前将节点释放，以至于我们不能找到其他的节点，但是我们采用后序遍历就完美的避免了这个问题，所以我们在释放二叉树时我们经常采用后序遍历的方式。

void BTNodeDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BTNodeDestory(root->left);
	BTNodeDestory(root->right);
	free(root);
}

2.13树的创建

BiTree* BiTreeCreate(BiTree* bt)
{
	bt = (BiTree*)malloc(sizeof(BiTree));
	char ch;
	scanf("%c", &ch);
	if (ch != '#')
	{
		bt->data = ch;
		bt->lchild = BiTreeCreate(bt);
		bt->rchild = BiTreeCreate(bt);
	}
	else
		bt = NULL;
	return bt;
}

3.二叉树的性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有个结点.
2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是 .
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 , 度为2的分支结点个数为 ,则有＝＋1
4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h= . (ps：是log以2
为底，n+1为对数)
5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对
于序号为i的结点有：
1. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
2. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
3. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子