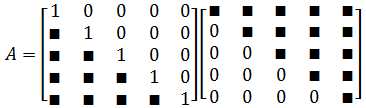C++红黑树封装set和map（很详细）

前言

在前面，我们学习了红黑树。（没学过红黑树直接看会很吃力）set和map的底层就是红黑树，现在我们要用这棵树来封装STL里面的容器：set和map。

下面是之前讲过的红黑树，他只是普通的“Key”模型,适合封装set容器

RBTree.h代码如下（这是之前的，还没封装好，后续会给上总代码）

#pragma once
 
enum color
{
	RED,
	BLACK
};
 
template<class K>
struct RBTreeNode
{
	RBTreeNode<K>* _parent;
	RBTreeNode<K>* _left;
	RBTreeNode<K>* _right;
	K _key;
	color _col;
	RBTreeNode(const K& key)
		:_key(key)
		,_parent(nullptr)
		,_left(nullptr)
		,_right(nullptr)
		,_col(RED)
	{}
};
 
template<class K>
class RBTree
{
	typedef RBTreeNode<K> Node;
public:
	bool Insert(const K& key)
	{
		Node* cur = _root;
		Node* parent = _root;
		if (_root == nullptr)
		{
			_root = new Node(key);
			_root->_col = BLACK;
			return true;
		}
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		if (parent->_key > key)
		{
			parent->_left = new Node(key);
			cur = parent->_left;
		}
		else
		{
			parent->_right = new Node(key);
			cur = parent->_right;
		}
		cur->_parent = parent;
		while (parent && parent->_col == RED)
		{
			Node* grandparent = parent->_parent;
 
			if (grandparent->_left == parent)
			{
				//     g
				//   p   u
				// c
				Node* uncle = grandparent->_right;
				if (uncle && uncle->_col == RED)
				{
					//变颜色
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandparent->_col = RED;
					//往上更新
					cur = grandparent;
					parent = grandparent->_parent;
				}
				else
				{
					//     g
					//   p   u
					// c
					if(cur == parent->_left)
					{
						RotateR(grandparent);
						grandparent->_col = RED;
						parent->_col = BLACK;
						break;
					}
					//      g
					//   p     u
					//    c
					else
					{
						RotateL(parent);
						RotateR(grandparent);
						cur->_col = BLACK;
						grandparent->_col = RED;
						break;
					}
				}
			}
			else  //grandparent->_right == parent
			{
				//     g
				//   u   p
				//         c
				Node* uncle = grandparent->_left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					cur = grandparent;
					parent = grandparent->_parent;
				}
				else
				{
					//     g
					//   u   p
					//         c
					if (parent->_right == cur)
					{
						RotateL(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
						break;
					}
					else
					{
						//     g
						//   u   p
						//      c
						RotateR(parent);
						RotateL(grandparent);
 
						cur->_col = BLACK;
						grandparent->_col = RED;
						break;
					}
				}
			}
		}
		_root->_col = BLACK;
		return true;
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
 
	bool Check(Node* root,int BlackNum,int valRef)
	{
		if (root == nullptr)
		{
			if(BlackNum == valRef)
			{
				return true;
			}
			else
			{
				cout << "每条路径黑色结点个数不等" << endl;
				return false;
			}
		}
		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "有连续的红色节点" << endl;
			return false;
		}
		if (root->_col == BLACK)
		{
			BlackNum++;
		}
		return Check(root->_left,BlackNum,valRef) && Check(root->_right, BlackNum, valRef);
	}
 
	bool IsBalance()
	{
		if (_root == nullptr)
			return true;
		if (_root->_col == RED)
			return false;
		int valRef = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				valRef++;
			cur = cur->_left;
		}
		int BlackNum = 0;
		return Check(_root,BlackNum,valRef);
	}
 
private:
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
		subL->_right = parent;
		Node* grandparent = parent->_parent;
		parent->_parent = subL;
		if (grandparent == nullptr)
		{
			_root = subL;
			subL->_parent = nullptr;
			return;
		}
		if (grandparent->_left == parent)
		{
			grandparent->_left = subL;
		}
		else
		{
			grandparent->_right = subL;
		}
		subL->_parent = grandparent;
	}
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		subR->_left = parent;
		Node* grandparent = parent->_parent;
		parent->_parent = subR;
		if (grandparent == nullptr)
		{
			_root = subR;
			_root->_parent = nullptr;
			return;
		}
		if (grandparent->_left == parent)
		{
			grandparent->_left = subR;
		}
		else
		{
			grandparent->_right = subR;
		}
		subR->_parent = grandparent;
	}
	Node* _root = nullptr;
};

一、修改模型

如果要封装map的“Key，Value” 容器，那么我们需要重新copy一份红黑树，改成“Key，Value” 模型去封装map，这样似乎也太笨了一点，我们看看写库函数的大佬是如何处理的。如何用一棵树封装map和set

这里提出了库里面的关键信息，其他内容看不懂没关系，只需要知道红黑树结点类型只有Value，通过类型Value来判断是“Key”还是“Key，Value”

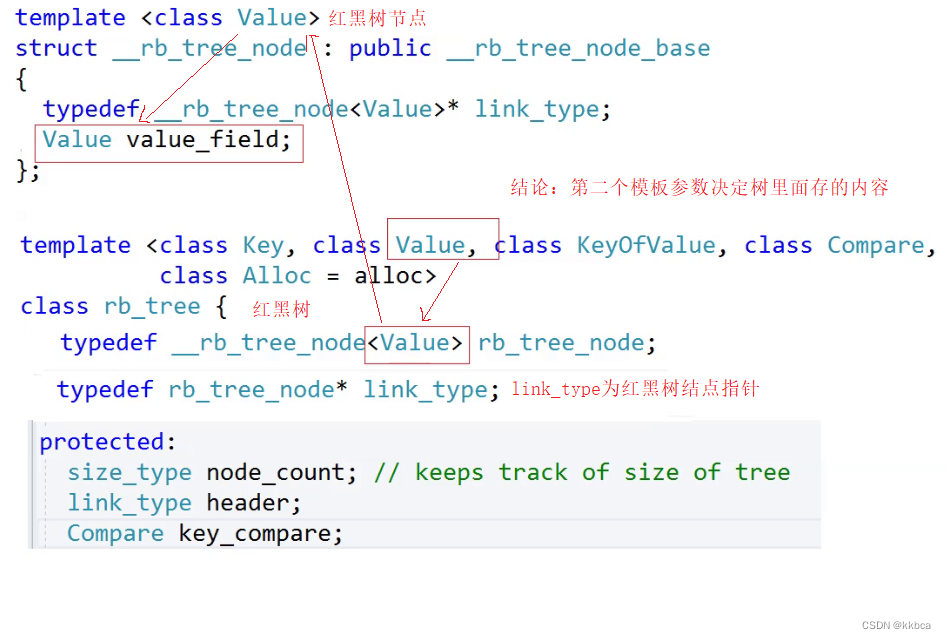
1.set传递的第二个参数

我们再看一下set容器所传递的内容是什么，可以看到对Key typedef了一下，给到红黑树的第二个参数value_type就是Key。这个value_type会传递给上面的Value。（注意看这里的私有成员是rb_tree类型的 t，调用的是上面图片的rb_tree）

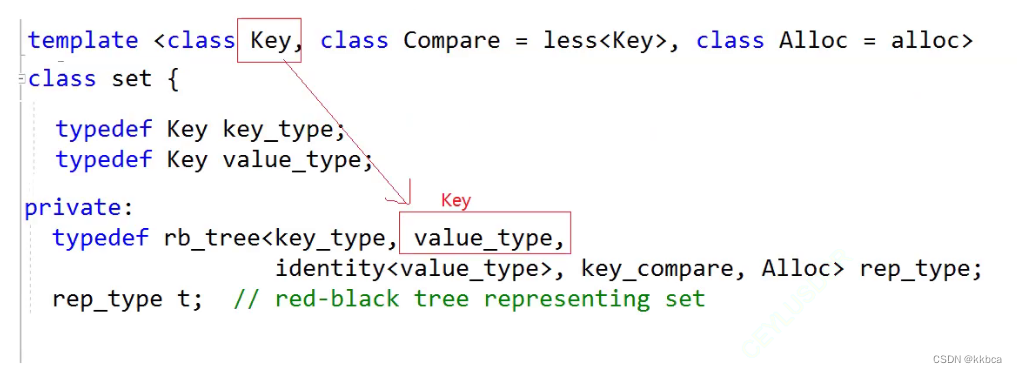
2.map传递的第二个参数

map容器 typedef 的value_type是pair<const Key,T>类型，因此map传递给红黑树的第二个参数为pair<const Key,T>类型。

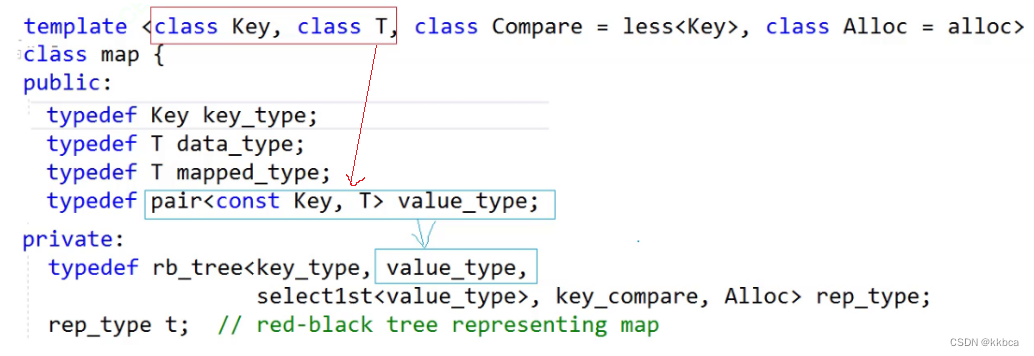
如此一来，可以通过一颗红黑树来实现“Key”和“Key，Value”模型。那么他具体是怎么实现的，我们还需要进一步分析

3.修改RBTree.h与添加map.h和set.h

根据库里面的内容，我们也对自己的RBTree.h代码进行修改

RBTreeNode结点，根据库里面的，将模板类型K改成了T，K _key改成T _data更容易理解，_data是什么，我们不知道，要看你具体传什么内容，可能是单个key，可能是pair。

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _parent;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	T _data;
	color _col;
	RBTreeNode(const T& data)
		:_data(data)
		,_parent(nullptr)
		,_left(nullptr)
		,_right(nullptr)
		,_col(RED)
	{}
};

对于RBTree也要进行改造，模板参数添加上T类型，插入具体的我只改了一点点，防止文章过与冗余，后面都要弄成data。（后续会给上总代码，大家先理解就好）

template<class K,class T>  //添加了T
class RBTree
{
	typedef RBTreeNode<T> Node;
    bool Insert(const T& data)  //修改部分
	{
		Node* cur = _root;
		Node* parent = _root;
		if (_root == nullptr)
		{
			_root = new Node(data);  //修改部分
			_root->_col = BLACK;
			return true;
		}
    .........//后续还有很多内容，这里就不多改造了
    }
}

写出set.h （仿函数不添加，防止混乱）跟库里面的一样，传递的第二个参数为K类型

#pragma once
#include"RBTree.h"
namespace kky
{
	template<class K>
	class set
	{
	private:
        RBTree<K, K> _t;
	};
}

写出map.h 跟库里面的一样，传递的第二个参数为pair类型

#pragma once
#include"RBTree.h"
namespace kky
{
	template<class K,class V>
	class map
	{
	private:
		RBTree<K, pair<const K, V>> _t;
	};
}

这里有点绕，现在我们再来捋一捋。

你是map，那么你传递的第二个参数T是pair，通过T构建出来的结点也是pair类型，里面存放的_data自然是pair类型。

你是set，你传递的第二个参数T是K，通过T构建出来的结点也是K类型，里面存放的_data自然是K类型。

4.仿函数取出set中的key和map中的key

那么现在问题又来了，这样就可以构建出来了吗？我们代码逻辑部分会不会有点问题？

大家看下面的代码，这是一个插入时的比较代码，看存放的数据比当前结点大还是小，如果大，往右走，如果小往左走，后面就是找到合适的地方再进行插入。

对于set来说，这句代码没有问题，可以这样比较。

对于map呢？map中的pair支不支持比较呢？我们去C++文档里面查一下，如下发现pair支持比较大小，但是他是first小就小，first如果相等，那么second小就小（这里代码使用了复用，仔细分析一下就是这个意思）

但是我们需要的不是这样啊，map我们只比较key，不比较value，如果key相等，就不要处理了，返回false（set和map的key不能重复）。库函数的比较我们用不上，我们需要自己写仿函数去判断。

现在的重点是将_data里面的key取出来比较。库里面是选择添加一个类型KeyOfValue。如下

那么具体是如何做到添加一个类模板对象，就做到可以如此比较的呢？（这里不懂没关系，下面我们还有图）

首先在set和map创建上KeyofValue类，目的是通过仿函数取出Key

set.h 添加上SetKeyofT，函数内部就是走个过场，直接取出key。并传递给RBTree，当做第三个参数。

public:
    struct SetKeyofT
    {
	    const K& operator()(const K& key)
	    {
	    	return key;
	    }
    };
private:
    RBTree<K, K,SetKeyofT> _t;

map.h 添加上MapKeyofT，目的是取出pair里面的first（也就是key），并将MapKeyofT传递给RBTree，当做第三个参数。

public:
	struct MapKeyofT
	{
		const K& operator()(const pair<const K, V>& kv)
		{
			return kv.first;
		}
	};
private:
	RBTree<K, pair<const K, V>,MapKeyofT> _t;

RBTree.h 修改，添加了第三个模板参数KeyofT，并使用KeyofT构建对象koft，对需要进行_data比较的地方，都是用koft仿函数处理。

template<class K,class T,class KeyOfT>
class RBTree
{
    KeyOfT koft;  //构建对象
	typedef RBTreeNode<T> Node;
public:
    pair<Node*,bool> Insert(const T& data)
    {
	    Node* cur = _root;
	    Node* parent = _root;
	    if (_root == nullptr)
	    {
		    _root = new Node(data);
		    _root->_col = BLACK;
		    return make_pair(_root,true) ;
	    }
	    while (cur)
	    {
		    if (koft(cur->_data) < koft(data))
		    {
			    parent = cur;
			    cur = cur->_right;
		    }
		    else if (koft(cur->_data) > koft(data))
		    {
			    parent = cur;
			    cur = cur->_left;
		    }
	        else
	        {
		        return make_pair(cur, false);
	        }
        }
        if (koft(parent->_data) > koft(data))
        {
	        parent->_left = new Node(data);
	        cur = parent->_left;
        }
        //后续内容没有比较，无需修改
    }
};

那么现在我们再画图捋一捋，

你是map，构建出的树第三个参数就是MapKeyofT，因此使用koft去调用_data数据，你获取的就是_data里面的first。

你是set，构建出的树第三个参数就是SetKeyofT，因此使用koft去调用_data数据，你获取的就是_data本身（这里的_data就是key）。

相当于set是陪太子读书，因为太子（map）需要使用koft去取出第一个数据，那么你set也得去这样取，就算你本身就是key，也这样跟这太子取，谁让他map是太子呢？

（这里逻辑其实并不复杂，只是有点点绕，大家不懂可以发评论问我）

注意：图片中的Insert函数返回类型大家看不懂可以忽略,当做bool就好，这是为了后续实现operator[]使用的（后面会讲）

到了现在，我们只需在set和map里面添加上insert函数就行，因为我们现在已经有了_t这颗树，因此调用_t树的Insert函数就好。

set.h 添加

bool Insert(const K& key)
{
	return _t.Insert(key);
}

map.h 添加

bool Insert(const pair<const K, V>& kv)
{
	return _t.Insert(kv);
}

现在就可以插入运行一下，看看我们封装得咋样了（iterator也不用管，后续会讲解，这里只做打印）

二、迭代器

1.迭代器基础

那么插入的基本逻辑，我们已经实现了，现在开搞迭代器，家人们，又是大坑来了，我们耐下性子慢慢来。

首先，map和set的迭代器只需要第二个参数------T 就可以了。他的成员函数只有红黑树结点_node，通过结点_node来进行构造迭代器，operator* 、 operator->、!=、==都很简单，这里我们不多赘述，代码如下

template<class T>
struct __TreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef __TreeIterator<T> Self;
	__TreeIterator(Node* node)
		:_node(node)
	{}
	T& operator*()
	{
		return _node->_data;
	}

	T* operator->()
	{
		return &_node->_data;
	}
    bool operator!=(const Self& s)
    {
	    return _node != s._node;
    }

    bool operator==(const Self& s)
    {
	    return _node == s._node;
    }
    Node* _node;
}

2.迭代器++

那么迭代器中很重要的++呢？

大家知道，在之前我们学习string、vector、list的时候，他们都是线性表，++往后面走就可以了，现在学到的set和map是树形结构，他的++应该如何走？

如图，it 在1的位置，那么it++，应该到6的地方去，那么我们可以知道，当前节点的右子树不为空，我们++需要到右子树的最左结点去。那么如果我们现在在6的地方，再++应该去到8的地方，那么我们又可以知道，当parent->right==cur时，我们需要再往上面走，一直走到parent->left == cur的时候才停止，再去遍历parent节点。不理解没关系，我们后面画图分析

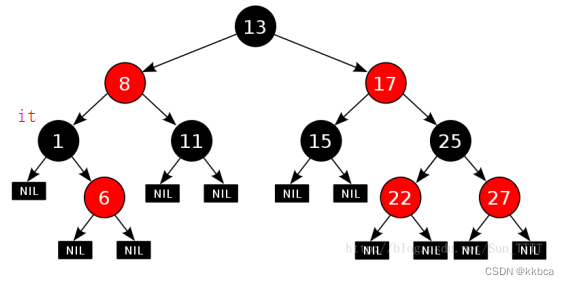
为什么会这样？因为中序是左根右，当前结点已经遍历完了，证明左和根已经遍历完毕，需要遍历右边，当右边遍历完毕，证明该树遍历完毕，也就是遍历完了父亲的左子树（该树就是左子树），应该去遍历父亲节点

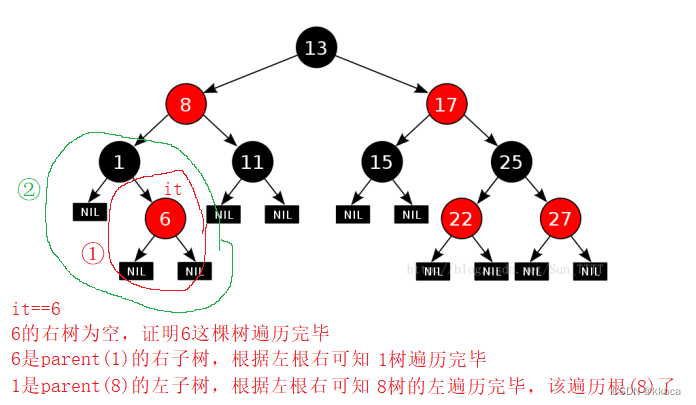
关键点是如果当前节点右为空，看当前节点是父亲的左还是右，是左就遍历父亲，是右就往上面走，知道当前节点是父亲的左。

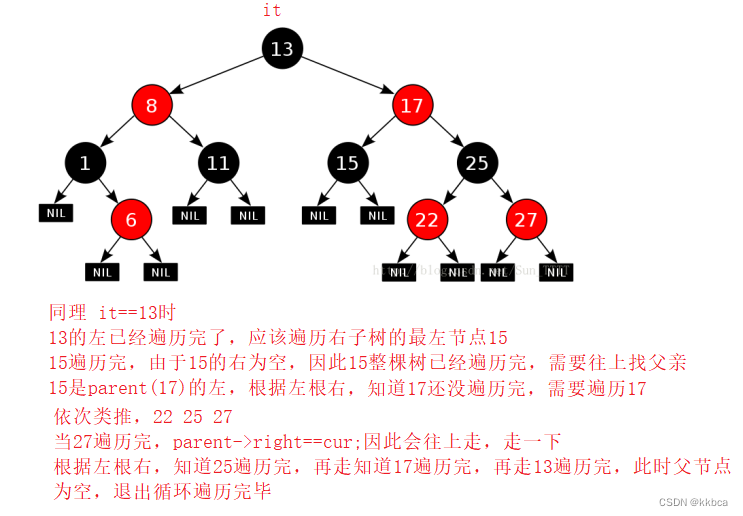
根据我们的分析，++代码如下 _node为迭代器成员变量

Self& operator++()
{
	if (_node->_right)  //右树存在  找右树最左节点
	{
		Node* cur = _node->_right;
		while (cur->_left)
		{
			cur = cur->_left;
		}
		_node = cur;
	}
	else    //右树不存在  往上迭代
	{
		Node* cur = _node;
		Node* parent = _node->_parent;
		while (parent && parent->_right == cur)
		{
			cur = parent;
			parent = parent->_parent;
		}
		_node = parent;
	}
	return *this;
}

3.迭代器--

迭代器--跟++不能说一模一样，只能说毫无差距，他们是相反的，直接上代码

Self& operator--()
{
	if (_node->_left)
	{
		Node* cur = _node->_left;
		while (cur->_right)
		{
			cur = cur->_right;
		}
		_node = cur;
	}
	else
	{
		Node* cur = _node;
		Node* parent = _node->_parent;
		while (parent && parent->_left == cur)
		{
			cur = parent;
			parent = parent->_parent;
		}
		_node = parent;
	}
	return *this;
}

4.添加begin()、end()

RBTree.h添加迭代器和begin()、end()

typedef __TreeIterator<T> iterator;
iterator begin()
{
	Node* cur = _root;
	while (cur && cur->_left)
	{
		cur = cur->_left;
	}
	return iterator(cur);
}

iterator end()
{
	return iterator(nullptr);
}

set.h

typedef RBTree<T>::iterator iterator;
iterator begin()
{
	return _t.begin();
}

iterator end()
{
	return _t.end();
}

map.h

typedef RBTree<pair<const K, V>>::iterator iterator;
iterator begin()
{
	return _t.begin();
}

iterator end()
{
	return _t.end();
}

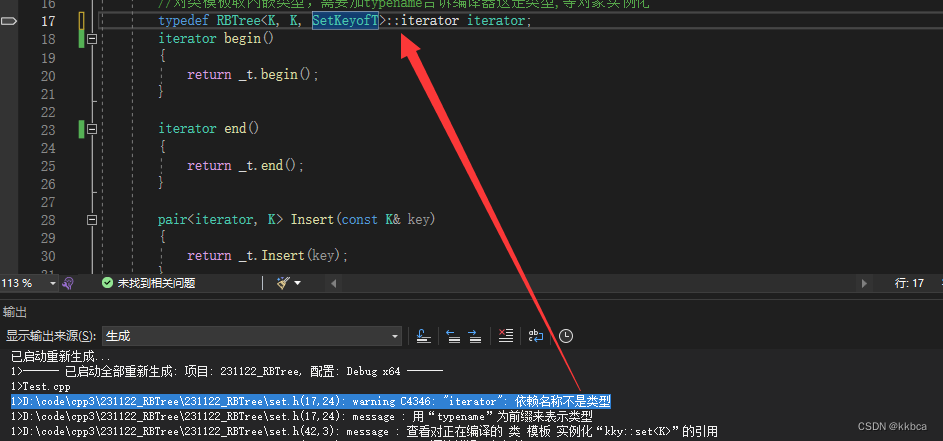
但是当我们编译时却报错了这是为什么呢？

首先，这个iterator是RBTree里面的，而RBTree里面的iterator也是typedef过的，是__TreeIterator里面的。

因此在set里面的RBTree<K, K, SetKeyofT>::iterator是内嵌类型，还没有实例化，编译器在编译时不知道他是什么类型，根本就不认识他，我们需要给set里面的RBTree<K, K, SetKeyofT>::iterator给添加上typename，告诉编译器这里是类型，你现在先不急着去找他，等到对象实例化的时候，你再去取出他的类型。如下
typedef typename RBTree<K,K,SetKeyofT>::iterator iterator;

现在迭代器才算构建好，set和map可以运行了。

三、map的operator[]

再把operator[]给实现一下，C++文档里面的operator[]如下

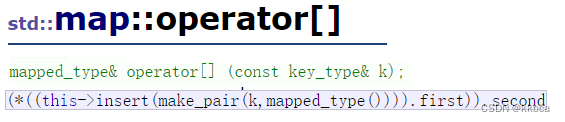
这里有点绕，看不懂很正常，我们拆分一下，如下

根据我们的分析，operator[]首先会执行插入，无论成功还是失败会取到该树的迭代器的Value。还有一点就是insert的返回类型为pair<iterator,bool>，之前为了代码简单，我们写的insert返回类型是bool。

因此我们需要修改insert的返回类型，同时修改函数内部return 后接上的内容，如下，下面还有的return也需要修改，这里不过多展开，不多赘述。

set.h也修改 map.h也修改

并在map.h里面添加上，我们写绕一点，更容易理解，库里面的大佬写法学不会。
V& operator[](const K& key)
{
	pair<iterator, bool> ret = Insert(make_pair(key, V()));
	return ret.first->second;
}

测试一下结果，nice完成啦！！！！

四、const迭代器

1.set的const迭代器

我们的代码还有一点点问题，如下，set的key竟然可以修改，这并不是我们想要的。

库里面set是如下处理的，首先在RBTree里添加了const迭代器，然后set里面的普通迭代器和const迭代器都是调用的RBTree里的const迭代器，目的就是不要修改key值。

至于为什么需要const迭代器，这是STL的规定，因为之前的容器都有const迭代器。

map是的处理如下，普通的就是普通的，const就是const的，普通的key不可以修改，value可以修改，const迭代器key和value都不可以修改

那么现在我们的目的是要把const迭代器搞出来。

在红黑树的迭代器中，我们只有T& 和T*要去取出节点里面的值，那么为了防止修改，只需要给这两个地方添加上const就可以了。但是如果仅仅给T传参的时候传const T，那么肯定是不符合要求的，因为这样我们创建的结点Node的类型也是const T，那岂不是会让Node里面的_data或者其他内容无法修改，这肯定不行我们想要的。

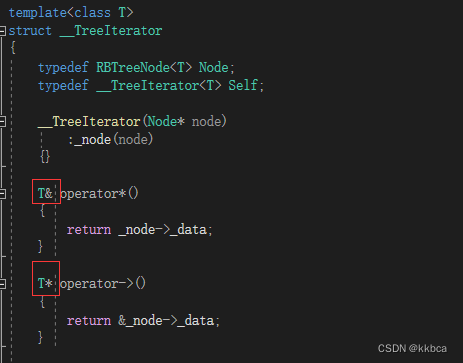
因此我们可以借鉴库里的方法，类模板传递三个参数，修改方法如下，普通的就传递<T,T*,T&>，const的就传递<T,const T*,const T&>，这样就符合我们的要求了，是普通迭代器里面的内容就可以修改，const的无法修改

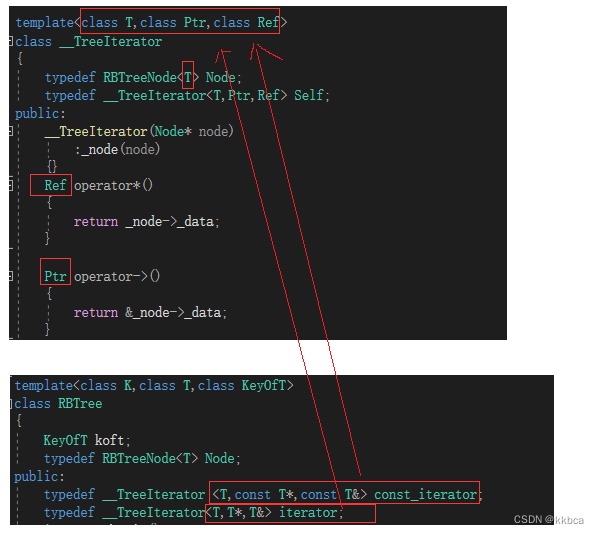
同时还得在RBTree里添加const版本的begin()和end()。如下

const_iterator begin() const 
{
	Node* cur = _root;
	while (cur && cur->_left)
	{
		cur = cur->_left;
	}
	return const_iterator(cur);
}

const_iterator end() const
{
	return const_iterator(nullptr);
}

同时在set里面修改一下，将iterator和const_iterator都typedef为RBTree里的const_iterator，这样就都没办法修改了，还有一点，我们并不需要再重写const_iterator的const版本的begin()和const版本的end()，因为虽然看着返回值是iterator，实际上被我们typedef成了const_iterator。只需要在结尾添加上const即可

现在我们就不能修改了。

但是现在我们取消了修改，代码还是报错了

报错内容为insert的时候类型匹配不上（注意，这里返回类型K写出了，应该为bool）

为什么会报这种错误呢？

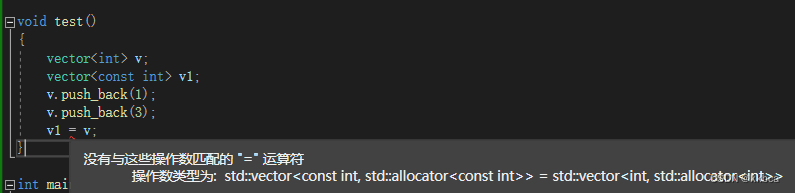
看下面分析，set里的iterator被我们typedef了，他的本质是const_iterator 模板类型为<T,const T*,const T&>，而RBTree里面的iterator就是iterator模板类型为<T, T*,T&>，他们类型不一样。（这里并不是权限缩小的问题，是类模板参数不一样）

有点难理解没关系，我们再看下面，这样看是不是就更清楚了他们类型不一样

2.解决方案1（解决了set）（建议直接看解决方案2）

那么对于这个报错我们可以如何修改呢？

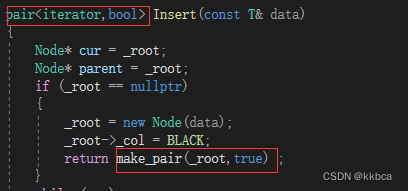
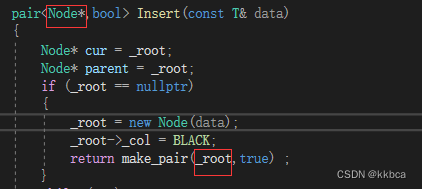
其实很简单，只需要将RBTree里面的返回类型和返回结果修改一下就好，如下

虽然看起来有那么一点点非主流，但是这确实是一个可行方案，并且很容易理解。

那么为什么这样修改就可以运行了呢？

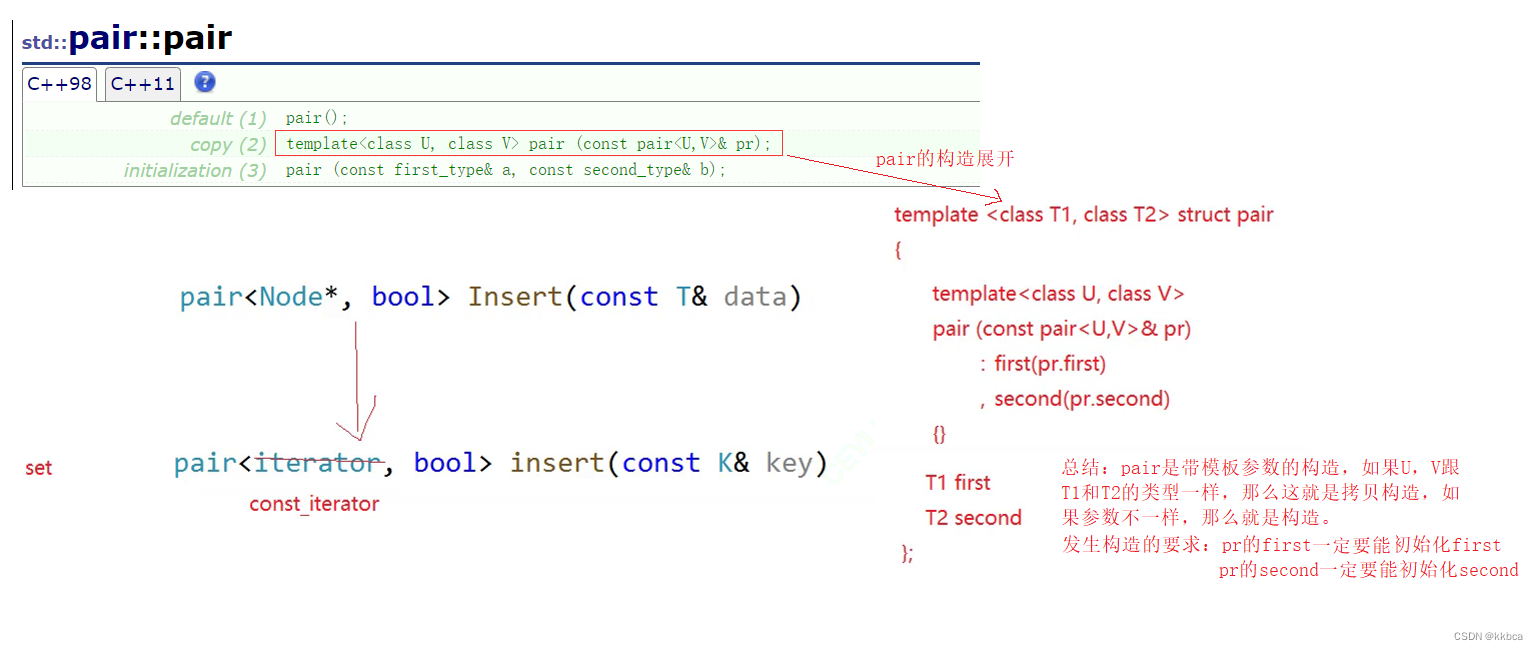
这就要提到pair的构造了，下面我们将pair的构造展开

现在分析一下，为什么pair<Node*,bool>能够初始化pair<const_iterator,bool>（第一个参数表面上是iterator，本质是const_iterator）？

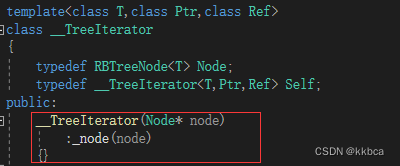
因为const_iterator也是可以通过Node*来构造。这是我们迭代器的构造函数啊,如下

下面我们再捋一捋流程图，看看是怎么构造的，首先，set调用了插入，会调用RBTree的插入，返回回来类型，发现pair的类型不同，不能拷贝构造，于是他会尝试看能不能进行构造，发现__TreeIterator有这么一个类，并且可以构造，于是就完成了iterator的构造了。

3.map的const迭代器

map的普通迭代器是key不能修改，而value可以修改，const迭代器是key和value都不可以修改，因此他不能像set一样，普通是const，const也是const。

我们在map里面添加上如下方框框起来的代码。

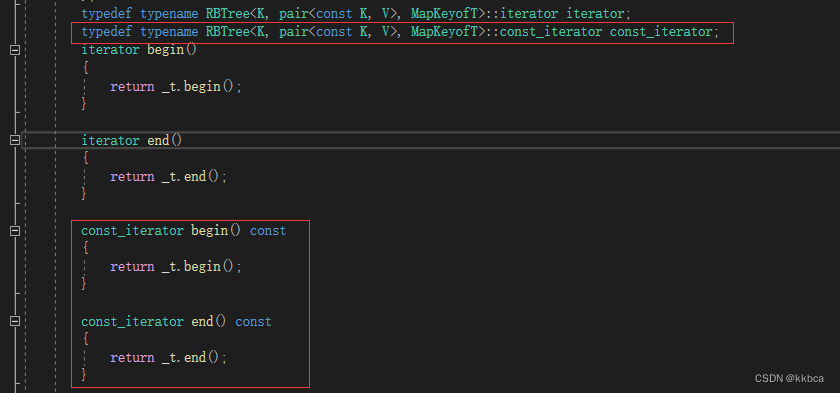
4.解决方案2（解决map和set）

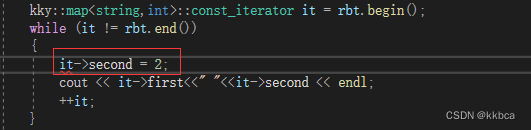
再去看一看能不能运行map的const迭代器，并且查看map的second是否可以修改

那我们再仔细看看为何报错？

他们的区别是多了两个const

也就是这一句

我们翻译一下，他的意思就是不能从普通迭代器变成const迭代器，所针对的就是如下代码，从iterator到const_iterator这条路行不通

那么我们应该如何修改呢？

首先我们应该要想到构造函数，我们写出一个从iterator到const_iterator的构造函数就好了。具体如何写，我们还是可以参考一下库里面的内容。

库里面是如何操作的？

首先用类模板的第一个参数构造typedef一个iterator。这代表着无论你传递的Ref和Ptr是普通的还是const版本的，经过我只取第一个参数typedef的操作，我都能保证他是普通的，那么我用普通迭代器来进行构造。

1.如果你传递的Ref和Ptr是普通的，我就相当于拷贝构造。

2.如果你传递的Ref和Ptr是const的，我就相当于从普通版本，构造成了const版本。

这样就符合我们的条件了。

那我们跟着库里面进行编写代码，写出如下代码。

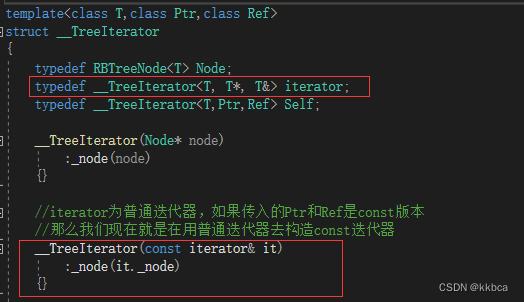
再查看就不报错了，只有不能修改的错误，我们代码删除就好了

测试运行，大功告成！！！

五、总结

回到之前的问题，为什么map和set的封装第一个参数需要K，能不能不要K？

先说答案，不能。虽然我们在insert插入函数里面并没有用到K类型，但如果是Find函数呢，你肯定是德通过Key类型去传递参数查找吧，我们所传递的第三个参数KeyOfT，他仅仅能取出第二参数T里面的内容，他不能推断T里面的参数类型，因此第一个参数K不能省略

map和set的封装并不比红黑树简单，需要肚兜理解，并且我们实现的还仅仅是简单版本，还有反向迭代器和除插入之外的函数都没有完成，但这一部分，也是足够我们学习红黑树和map、set的性质了。希望与大家共勉！！！

最后附上总代码

RBTree.h

#pragma once

enum color
{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _parent;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	T _data;
	color _col;
	RBTreeNode(const T& data)
		:_data(data)
		,_parent(nullptr)
		,_left(nullptr)
		,_right(nullptr)
		,_col(RED)
	{}
};

template<class T,class Ptr,class Ref>
struct __TreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef __TreeIterator<T, T*, T&> iterator;
	typedef __TreeIterator<T,Ptr,Ref> Self;

	__TreeIterator(Node* node)
		:_node(node)
	{}

	//iterator为普通迭代器，如果传入的Ptr和Ref是const版本
	//那么我们现在就是在用普通迭代器去构造const迭代器
	__TreeIterator(const iterator& it) 
		:_node(it._node)
	{}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &_node->_data;
	}

	Self& operator++()
	{
		if (_node->_right)
		{
			Node* cur = _node->_right;
			while (cur->_left)
			{
				cur = cur->_left;
			}
			_node = cur;
		}
		else
		{
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent && parent->_right == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}

	Self& operator--()
	{
		if (_node->_left)
		{
			Node* cur = _node->_left;
			while (cur->_right)
			{
				cur = cur->_right;
			}
			_node = cur;
		}
		else
		{
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent && parent->_left == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}

	bool operator==(const Self& s)
	{
		return _node == s._node;
	}

	Node* _node;
};


// set->RBTree<K,K,SetKeyOfT> _t;
// map->RBTree<K.pair<K,T>,MapKeyOfT> _t;
template<class K,class T,class KeyOfT>
class RBTree
{
	KeyOfT koft;
	typedef RBTreeNode<T> Node;
public:
	typedef __TreeIterator <T,const T*,const T&> const_iterator;
	typedef __TreeIterator<T,T*,T&> iterator;
	iterator begin()
	{
		Node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return iterator(cur);
	}

	iterator end()
	{
		return iterator(nullptr);
	}

	const_iterator begin() const 
	{
		Node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return const_iterator(cur);
	}

	const_iterator end() const
	{
		return const_iterator(nullptr);
	}

	pair<iterator,bool> Insert(const T& data)
	{
		Node* cur = _root;
		Node* parent = _root;
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(_root,true) ;
		}
		while (cur)
		{
			if (koft(cur->_data) < koft(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (koft(cur->_data) > koft(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return make_pair(cur, false);
			}
		}
		if (koft(parent->_data) > koft(data))
		{
			parent->_left = new Node(data);
			cur = parent->_left;
		}
		else
		{
			parent->_right = new Node(data);
			cur = parent->_right;
		}
		cur->_parent = parent;
		while (parent && parent->_col == RED)
		{
			Node* grandparent = parent->_parent;

			if (grandparent->_left == parent)
			{
				//     g
				//   p   u
				// c
				Node* uncle = grandparent->_right;
				if (uncle && uncle->_col == RED)
				{
					//变颜色
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandparent->_col = RED;
					//往上更新
					cur = grandparent;
					parent = grandparent->_parent;
				}
				else
				{
					//     g
					//   p   u
					// c
					if(cur == parent->_left)
					{
						RotateR(grandparent);
						grandparent->_col = RED;
						parent->_col = BLACK;
						break;
					}
					//      g
					//   p     u
					//    c
					else
					{
						RotateL(parent);
						RotateR(grandparent);
						cur->_col = BLACK;
						grandparent->_col = RED;
						break;
					}
				}
			}
			else  //grandparent->_right == parent
			{
				//     g
				//   u   p
				//         c
				Node* uncle = grandparent->_left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					cur = grandparent;
					parent = grandparent->_parent;
				}
				else
				{
					//     g
					//   u   p
					//         c
					if (parent->_right == cur)
					{
						RotateL(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
						break;
					}
					else
					{
						//     g
						//   u   p
						//      c
						RotateR(parent);
						RotateL(grandparent);

						cur->_col = BLACK;
						grandparent->_col = RED;
						break;
					}
				}
			}
		}
		_root->_col = BLACK;
		return make_pair(cur, false);
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	bool Check(Node* root,int BlackNum,int valRef)
	{
		if (root == nullptr)
		{
			if(BlackNum == valRef)
			{
				return true;
			}
			else
			{
				cout << "每条路径黑色结点个数不等" << endl;
				return false;
			}
		}
		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "有连续的红色节点" << endl;
			return false;
		}
		if (root->_col == BLACK)
		{
			BlackNum++;
		}
		return Check(root->_left,BlackNum,valRef) && Check(root->_right, BlackNum, valRef);
	}

	bool IsBalance()
	{
		if (_root == nullptr)
			return true;
		if (_root->_col == RED)
			return false;
		int valRef = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				valRef++;
			cur = cur->_left;
		}
		int BlackNum = 0;
		return Check(_root,BlackNum,valRef);
	}

private:
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		cout << root->_data << " ";
		_InOrder(root->_right);
	}
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
		subL->_right = parent;
		Node* grandparent = parent->_parent;
		parent->_parent = subL;
		if (grandparent == nullptr)
		{
			_root = subL;
			subL->_parent = nullptr;
			return;
		}
		if (grandparent->_left == parent)
		{
			grandparent->_left = subL;
		}
		else
		{
			grandparent->_right = subL;
		}
		subL->_parent = grandparent;
	}
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		subR->_left = parent;
		Node* grandparent = parent->_parent;
		parent->_parent = subR;
		if (grandparent == nullptr)
		{
			_root = subR;
			_root->_parent = nullptr;
			return;
		}
		if (grandparent->_left == parent)
		{
			grandparent->_left = subR;
		}
		else
		{
			grandparent->_right = subR;
		}
		subR->_parent = grandparent;
	}
	Node* _root = nullptr;
};

set.h

#pragma once
#include"RBTree.h"
namespace kky
{
	template<class K>
	class set
	{
	public:
		struct SetKeyofT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
		//对类模板取内嵌类型，需要加typename告诉编译器这是类型,等对象实例化
		typedef typename RBTree<K,K,SetKeyofT>::const_iterator iterator;
		typedef typename RBTree<K,K,SetKeyofT>::const_iterator const_iterator;
		iterator begin() const
		{
			return _t.begin();
		}

		iterator end() const
		{
			return _t.end();
		}

		pair<iterator, bool> Insert(const K& key)
		{
			return _t.Insert(key);
		}
		bool IsBalance()
		{
			return _t.IsBalance();
		}
		void InOrder()
		{
			_t.InOrder();
		}
	private:RBTree<K, K,SetKeyofT> _t;
	};
}

map.h

#pragma once
#include"RBTree.h"
namespace kky
{
	template<class K,class V>
	class map
	{
	public:
		struct MapKeyofT
		{
			const K& operator()(const pair<const K, V>& kv)
			{
				return kv.first;
			}
		};
		typedef typename RBTree<K, pair<const K, V>, MapKeyofT>::iterator iterator;
		typedef typename RBTree<K, pair<const K, V>, MapKeyofT>::const_iterator const_iterator;
		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		const_iterator begin() const
		{
			return _t.begin();
		}

		const_iterator end() const
		{
			return _t.end();
		}

		pair<iterator, bool> Insert(const pair<K, V>& kv)
		{
			return _t.Insert(kv);
		}
		bool IsBalance()
		{
			return _t.IsBalance();
		}
		void InOrder()
		{
			_t.InOrder();
		}
		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = Insert(make_pair(key, V()));
			return ret.first->second;
		}
	private:
		RBTree<K, pair<const K, V>,MapKeyofT> _t;
	};
}

Test.cpp

#include<iostream>
#include<vector>
#include<ctime>
using namespace std;
#include"RBTree.h"
#include"map.h"
#include"set.h"

void set_test()
{
	//const int N = 10;
	//vector<int> v;
	//v.reserve(N);
	//srand(time(0));
	//for (size_t i = 0; i < N; i++)
	//{
	//	v.push_back(rand() + i);
	//}
	//kky::set<int> rbt;
	//for (auto e : v)
	//{
	//	if (e == 24473)
	//	{
	//		int i = 0;
	//	}
	//	rbt.Insert(e);
	//	rbt.IsBalance();
	//}
	//rbt.InOrder();
	//cout << rbt.IsBalance() << endl;

	kky::set<int> rbt;
	rbt.Insert(4);
	rbt.Insert(6);
	rbt.Insert(5);
	rbt.Insert(3);
	kky::set<int>::const_iterator it = rbt.begin();
	while (it != rbt.end())
	{
		cout << *it << endl;
		++it;
	}
}

void map_test()
{
	string arr[] = {"香蕉","苹果","橘子","香蕉","苹果" ,"香蕉","苹果" ,"香蕉" };
	kky::map<string,int> rbt;
	for (auto e : arr)
	{
		rbt[e]++;
	}
	kky::map<string,int>::const_iterator it = rbt.begin();
	while (it != rbt.end())
	{
		cout << it->first<<" "<<it->second << endl;
		++it;
	}
	//kky::map<string, string> dict;
	//dict.Insert(make_pair("sort", "排序"));
	//dict.Insert(make_pair("sort", "xx"));
	//dict.Insert(make_pair("left", "左"));
	//dict.Insert(make_pair("right", "右"));
	//kky::map<string,string>::iterator it = dict.begin();
	//while (it != dict.end())
	//{
	//	cout << it->first<<" "<<it->second << endl;
	//	++it;
	//}
}

int main()
{
	set_test();
	map_test();
}

最后感谢大家的观看！！！！