LeetCode-470. 用 Rand7 实现 Rand10【数学 拒绝采样 概率与统计 随机化】
- 题目描述:
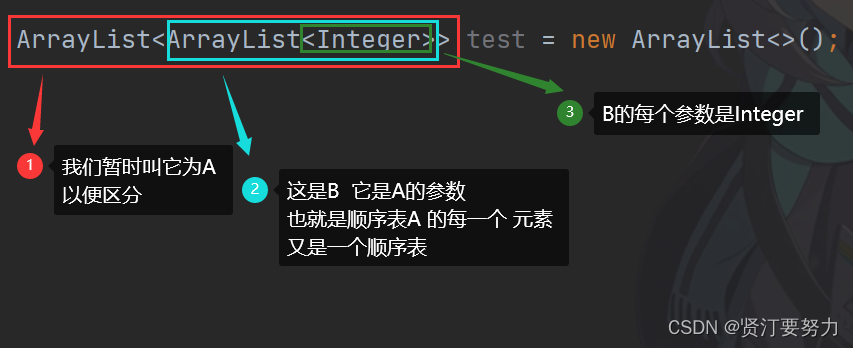
- 解题思路一:首先说一个结论就是`(rand_X() - 1) × Y + rand_Y() ==> [1,X*Y]`,即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数,Y是每一行的人数,X是列数【参考下面的图】。第二就是拒绝采样,效果是能够减少调用rand7()的调用次数。我们在利用`(rand_7() - 1) × 7 + rand_7() ==> [1,7*7]`得到rand49()的时候,我们希望能够等概率的生成[1,10]的随机数,那么可以拒绝掉大于40的数。即`if num<=40:`才进行采样。
- 解题思路二:0
- 解题思路三:0
题目描述:
给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。
你只能调用 rand7() 且不能调用其他方法。请不要使用系统的 Math.random() 方法。
每个测试用例将有一个内部参数 n,即你实现的函数 rand10() 在测试时将被调用的次数。请注意,这不是传递给 rand10() 的参数。
示例 1:
输入: 1
输出: [2]
示例 2:
输入: 2
输出: [2,8]
示例 3:
输入: 3
输出: [3,8,10]
提示:
1 <= n <= 105
进阶:
rand7()调用次数的 期望值 是多少 ?
你能否尽量少调用 rand7() ?
解题思路一:首先说一个结论就是(rand_X() - 1) × Y + rand_Y() ==> [1,X*Y],即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数,Y是每一行的人数,X是列数【参考下面的图】。第二就是拒绝采样,效果是能够减少调用rand7()的调用次数。我们在利用(rand_7() - 1) × 7 + rand_7() ==> [1,7*7]得到rand49()的时候,我们希望能够等概率的生成[1,10]的随机数,那么可以拒绝掉大于40的数。即if num<=40:才进行采样。

为了充分利用被拒绝的采样结果,即舍弃掉[41, 49]这9个数。我们可以使用a = num - 40得到rand9,从而可以得到(rand_9() - 1) × 7 + rand_7() ==> [1,9*7]得到rand63,从而对rand63进行采样。这样之后的就不难理解了。
# The rand7() API is already defined for you.
# def rand7():
# @return a random integer in the range 1 to 7
class Solution:
def rand10(self):
"""
:rtype: int
"""
while True:
a = rand7()
b = rand7()
num = (a-1)*7 + b # rand49
if num<=40:
return num%10 + 1
a = num - 40 # rand9
b = rand7()
num = (a-1)*7 + b # rand63
if num<=60:
return num%10 + 1
a = num - 60 # rand3
b = rand7()
num = (a-1)*7 + b # rand21
if num<=20:
return num%10 + 1
时间复杂度:期望时间复杂度为O(1),但最坏情况下会达到 (∞)(一直被拒绝)。
空间复杂度:O(1)
分析一下rand7()调用次数的 期望值:
首先调用2次得到a,b
然后拒绝采样一次概率是9/49
第二次是9/49 * 3/63
第三次是9/49 * 3/63 * 1/21就是进入下一轮while循环了。所以是一个等比数列。
a
=
2
+
9
49
+
9
49
⋅
3
63
/
/
是每次采样成功的概率
b
=
9
49
⋅
3
63
⋅
1
21
/
/
是每次进入下一轮循环的概率(等比数列的公比)
E
(
#
c
a
l
l
)
=
a
⋅
1
1
−
b
≈
2.19333
\begin{align} a &= 2 + \frac{9}{49}+\frac{9}{49}·\frac{3}{63} \quad // \text{是每次采样成功的概率} \notag \\ b &= \frac{9}{49}·\frac{3}{63}·\frac{1}{21} \quad // \text {是每次进入下一轮循环的概率(等比数列的公比)} \notag \\ E(\#call) &= a·\frac{1}{1-b} \notag \\ &\approx 2.19333 \end{align}
abE(#call)=2+499+499⋅633//是每次采样成功的概率=499⋅633⋅211//是每次进入下一轮循环的概率(等比数列的公比)=a⋅1−b1≈2.19333
所以期望次数是2.19332
解题思路二:0
解题思路三:0