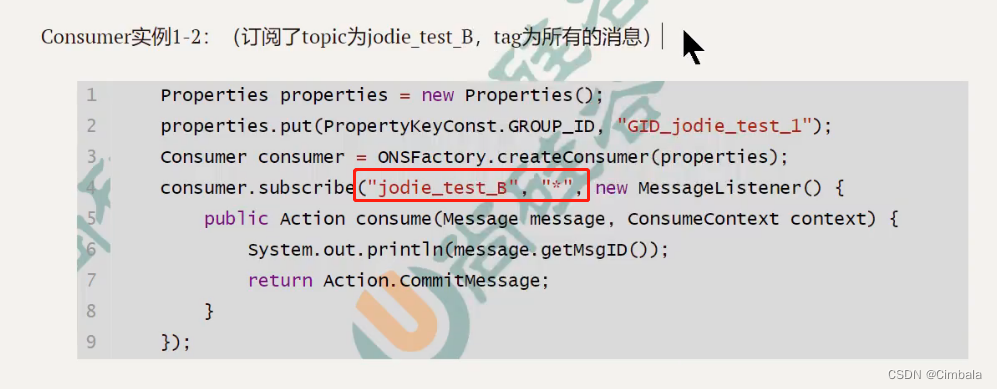
考场就座【LC855】

There is an exam room with n seats in a single row labeled from 0 to n - 1.

When a student enters the room, they must sit in the seat that maximizes the distance to the closest person. If there are multiple such seats, they sit in the seat with the lowest number. If no one is in the room, then the student sits at seat number 0.

Design a class that simulates the mentioned exam room.

Implement the ExamRoom class:

• ExamRoom(int n) Initializes the object of the exam room with the number of the seats n.
• int seat() Returns the label of the seat at which the next student will set.
• void leave(int p) Indicates that the student sitting at seat p will leave the room. It is guaranteed that there will be a student sitting at seat p.

复杂度还可以，至少比官方题解好，希望没分析错

• 思路：

  2022/12/30

  • 由于每次就座时，有三种情况：
    1. 无人就座：坐在0号座位
    2. 1人就座：坐在0号或者n-1号座位
    3. 2人及以上就座：就座座位与相邻两个座位的最小距离最大，因此可以在已就座的座位中找到相邻两个座位距离一半的最大值$dis$，并记录前一个座位在序号$preSeat$，新座位序号即为$preSeat+dis$。
  • 可以使用哈希表记录每个座位是否有人入座，但是当n很大时，每次在搜索距离的时候，不可避免的会搜索到未就座的座位，时间复杂度为O(n)；因此我使用动态数组$isSeated$记录已经就座的座位序号，并手动保证数组为升序排列（也可以使用TreeSet 做的时候没想到…），然后遍历数组，按照规律就座以及移除座位序号。

• 实现

  • 初始化：记录位置数量$n$

  • seat

    1. 情况1：$isSeated$大小为0，在0号座位就座

    2. 合并情况2和情况3：

       每次就座时在$preSeat$的后方插入新座位，因此记录$preSeat$在数组中的下标$preIndex$，在其后方插入新座位，保证数组为升序排列

       • 首先在已就座的座位中找到相邻两个座位距离一半的最大值dis，并记录preIndex
       • 然后处理0号座位未就座的情况，此时的距离为isSeated.get(0)，若isSeated.get(0)>dis，那么更新dis以及preIndex
       • 再处理n-1号座位未就座的情况，此时的距离为n- 1 - isSeated.get(size - 1)，若n- 1 - isSeated.get(size - 1)>dis，那么更新dis以及preIndex
       • 最后将该位置添加至数组中的相应位置

       （也可以在数组中添加哑结点，就不用额外处理了）

  • leave：二分查找座位p的下标，通过remove删除

  class ExamRoom {
      int n;
      // boolean[] isSeated;
      List<Integer> isSeated;
      public ExamRoom(int n) {
          // isSeated = new boolean[n];
          isSeated = new ArrayList<>();
          this.n = n;
      }
  
      public int seat() {
          int size = isSeated.size();
          if (size == 0){
              isSeated.add(0);
              return 0;
          }
          // else if (size == 1){
          //     int temp = isSeated.get(0);
          //     if (isSeated.get(0) < n / 2){
          //         isSeated.add(1, n - 1);
          //         return n - 1;
          //     }else{
          //         isSeated.add(0, 0);
          //         return 0;
          //     }
          // }
          int dis = 0;
          int preIndex = -1;
          // 首位
          if (isSeated.get(0) != 0 ){
              dis = isSeated.get(0);
          }
          for (int i = 0; i < size - 1; i++){
              int temp = (isSeated.get(i + 1) - isSeated.get(i)) / 2;
              if (dis < temp){
                  dis = temp;
                  preIndex = i;
              }
          }
          // 末尾
          if (n - 1 - isSeated.get(size - 1) > dis){
              dis = n - 1 - isSeated.get(size - 1);
              preIndex = size - 1;
          }
          int ans = preIndex == -1 ? 0 : isSeated.get(preIndex) + dis;
          isSeated.add(preIndex + 1, ans);
          return ans;
      }
  
      public void leave(int p) {
          int l = 0, r = isSeated.size() - 1;
          while (l <= r){
              int mid = (l + r) >> 1;
              if (isSeated.get(mid) == p){
                  isSeated.remove(mid);
                  return;
              }else if (isSeated.get(mid) > p){
                  r = mid - 1;
              }else{
                  l = mid + 1;
              }
          }
      }
  }
  

  • 复杂度

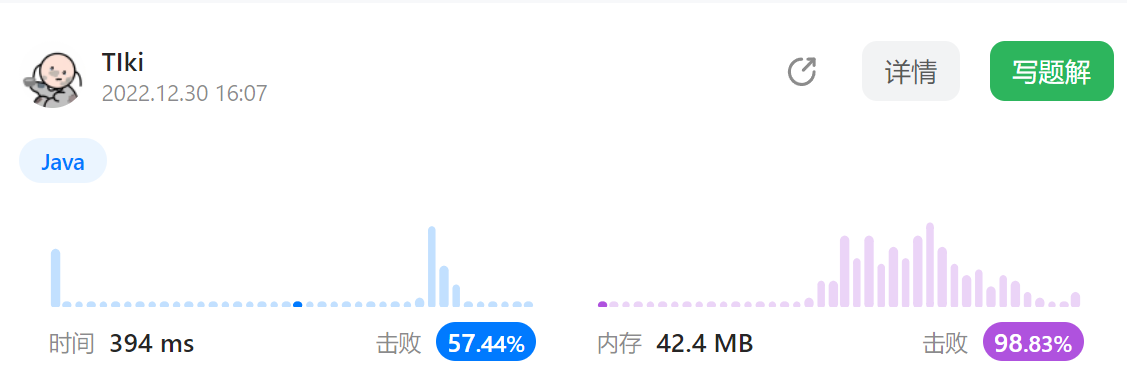
    • 时间复杂度：seat函数的时间复杂度为$O(P)$，每次都需要遍历整个动态数组，每次add添加元素的时间复杂度为$O(P)$。leave函数的时间复杂度为$O(P+logP)$，二分查找的时间复杂度为$O(logP)$，remove时间复杂度为$O(P)$。
    • 空间复杂度：$O(P)$

    

• TreeSet

  class ExamRoom {
      int N;
      TreeSet<Integer> students;
  
      public ExamRoom(int N) {
          this.N = N;
          students = new TreeSet();
      }
  
      public int seat() {
          //Let's determine student, the position of the next
          //student to sit down.
          int student = 0;
          if (students.size() > 0) {
              //Tenatively, dist is the distance to the closest student,
              //which is achieved by sitting in the position 'student'.
              //We start by considering the left-most seat.
              int dist = students.first();
              Integer prev = null;
              for (Integer s: students) {
                  if (prev != null) {
                      //For each pair of adjacent students in positions (prev, s),
                      //d is the distance to the closest student;
                      //achieved at position prev + d.
                      int d = (s - prev) / 2;
                      if (d > dist) {
                          dist = d;
                          student = prev + d;
                      }
                  }
                  prev = s;
              }
  
              //Considering the right-most seat.
              if (N - 1 - students.last() > dist)
                  student = N - 1;
          }
  
          //Add the student to our sorted TreeSet of positions.
          students.add(student);
          return student;
      }
  
      public void leave(int p) {
          students.remove(p);
      }
  }
  
  作者：力扣 (LeetCode)
  链接：https://leetcode.cn/problems/exam-room/solutions/20105/kao-chang-jiu-zuo-by-leetcode/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
  

  • 复杂度

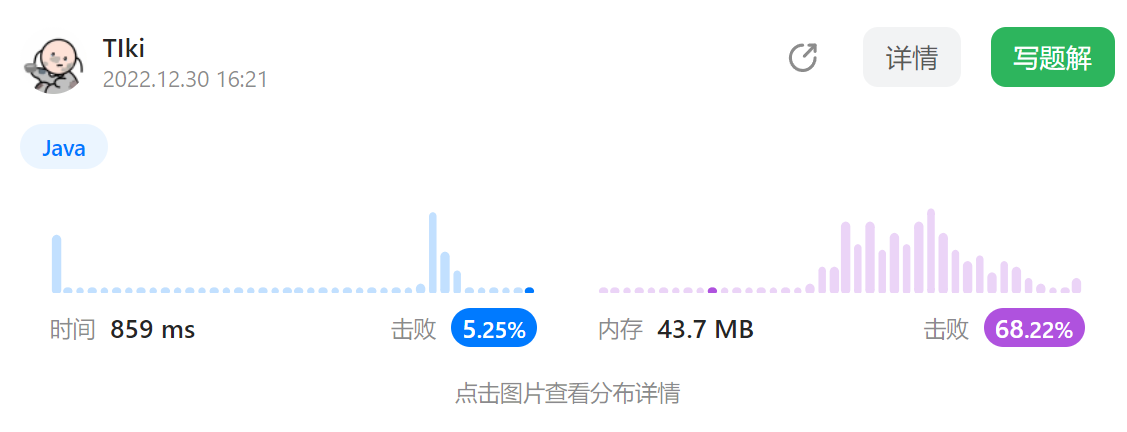
    • 时间复杂度：seat函数的时间复杂度为$O(P+logP)$，每次都需要遍历整个动态数组，每次add添加元素的时间复杂度为$O(logP)$。leave函数的时间复杂度为$O(logP)$，remove时间复杂度为$O(logP)$。
    • 空间复杂度：$O(P)$