1. 2d transformations
1.1缩放(Scaling)
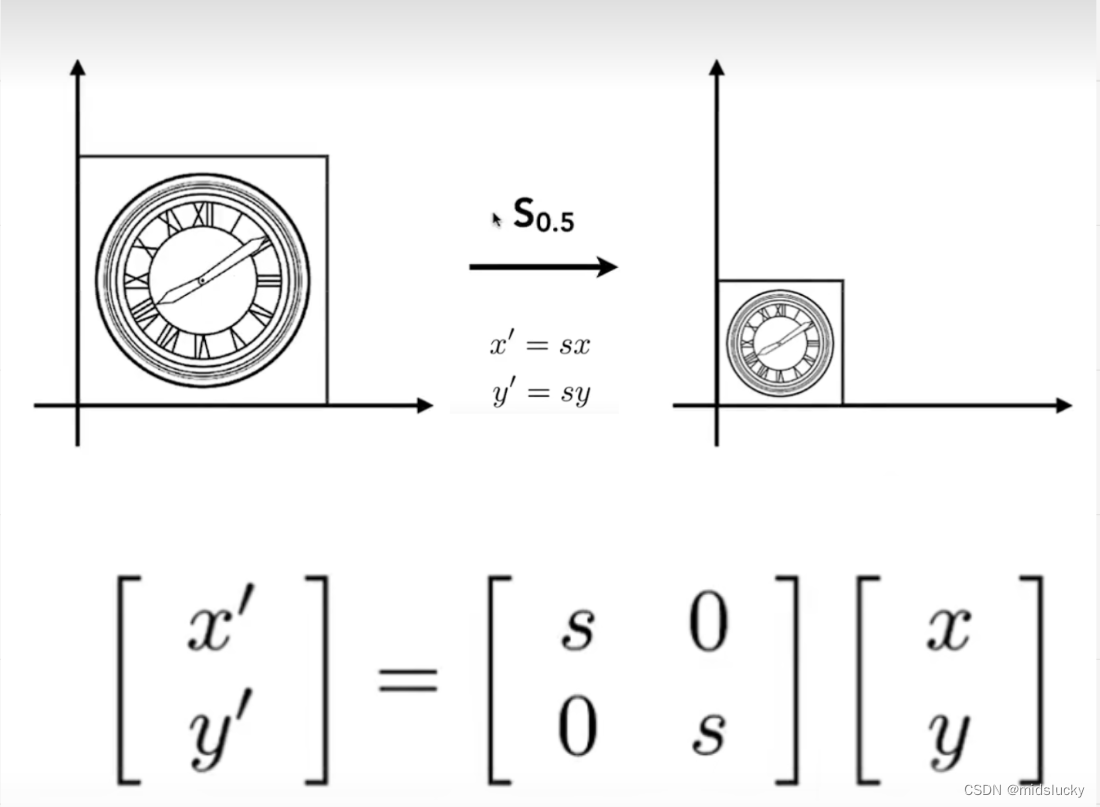
其实这个转换非常简单,如图所示就是把x与y进行s倍的缩放,而我们图中的这个矩阵正好满足这一算法。
1.2镜像(Reflection)

这个镜像变换可以和上面的做类比,简单看一下就行。
1.3错切(Shearing)
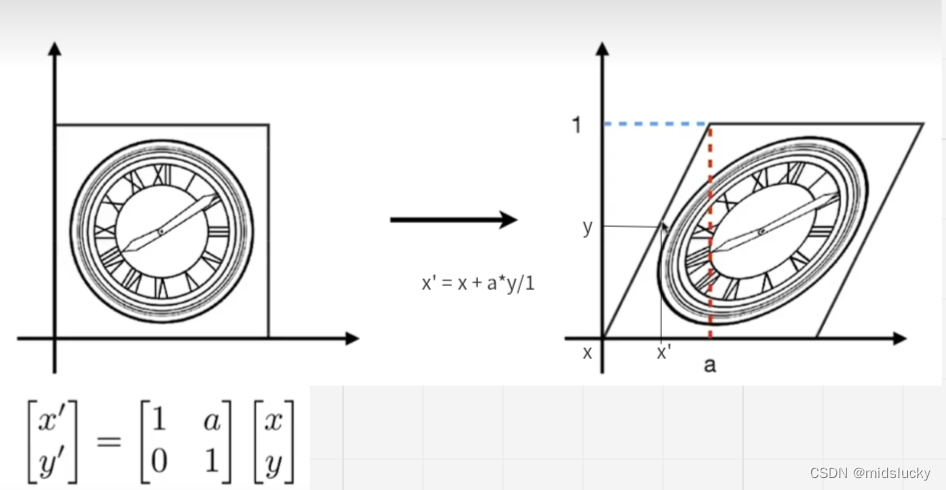
当然这里不得不提两句,这个错切可以这么看,如左图未转换前最左边的一条竖直直线,按照这样的转换思路在右边就变成了一条斜线,其他线段以此类推。
其实可以想象成如左边这条x等于0的竖直线,这上面的一个个点往右边平移了ay个单位,变成了这样一条斜线。
这里提一个有趣的想法:
如果把一条直线看成是由有限的等大小的点组成(在计算机中当然实际当中我们对直线的定义还是无数个点组成的图形),那么经过我们如上线性变换的时候,每个点的坐标发生了变换最后构成了一条斜线(比如说3个点构成了一条直线,现在把这三个点的位置挪动了下,这样点与点之间实际上会有距离间隔,但是实际我们的屏幕看不出这个距离间隔)
让我们在更加形象的来了解一下
我们知道计算机是由一个个像素组成的,如下图所示:

一条直线的长度等于这一个个正方形小像素的变成之和,而通过我们的图形变换我们改变了这一个个小像素的实际位置(可以把一个小像素看成一个单位坐标),如我们上面转换成的斜线的长度就是这一个个小像素的斜边加起来的值。
1.4旋转(Rotation)
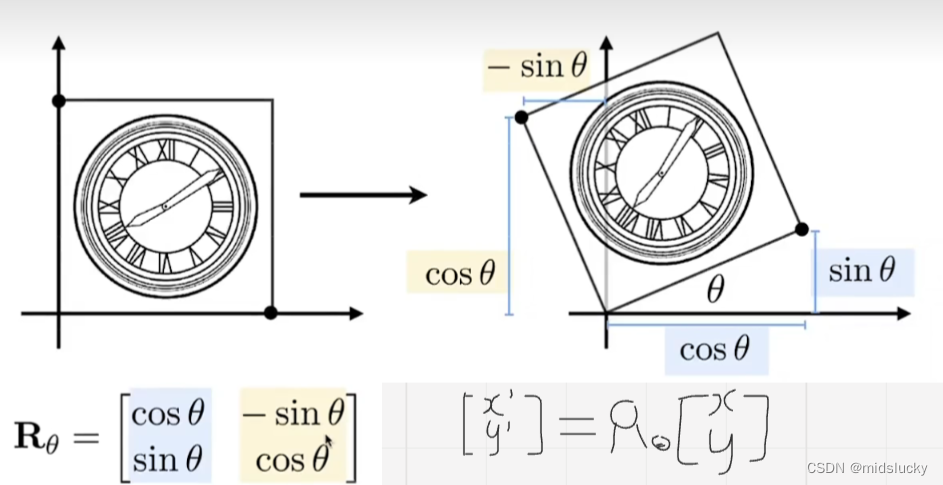
这里的推导非常简单,通过两个特例点`来将变换的矩阵推导出来,因为过于简单这里就不做过多赘述。(旋转我们默认是按圆点逆时针旋转)
这里留一个问题给大家,你怎么知道你特例点推出来矩阵后,你的图像整体都是如图上的规律变换的?
1.5平移(Translation)

按照我们上面的例子依葫芦画瓢就可以很轻易的得出如图所示的式子,但是这个式子后面多了一个矩阵,这样的表达式看着不是很简明了,为了处理这样的问题,我们的图形学引入了对向量和点的新的表达形式来解决了这一问题。
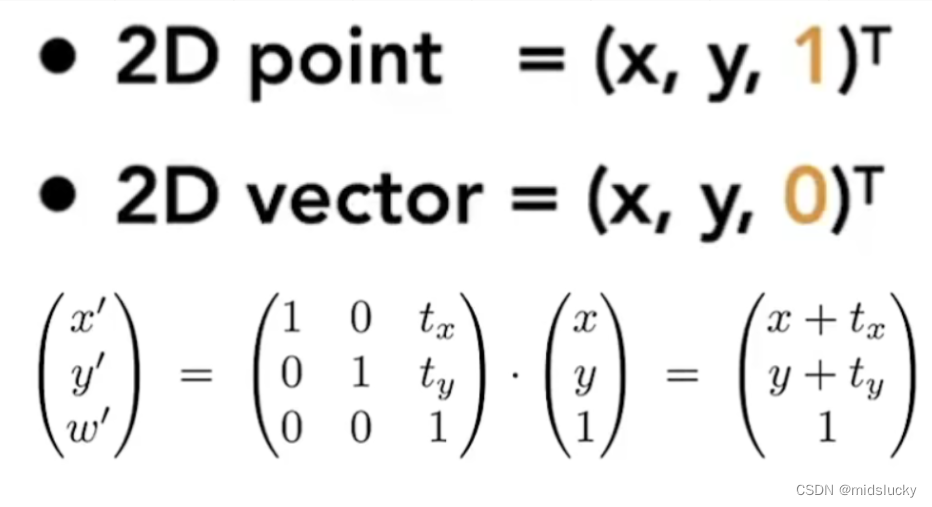
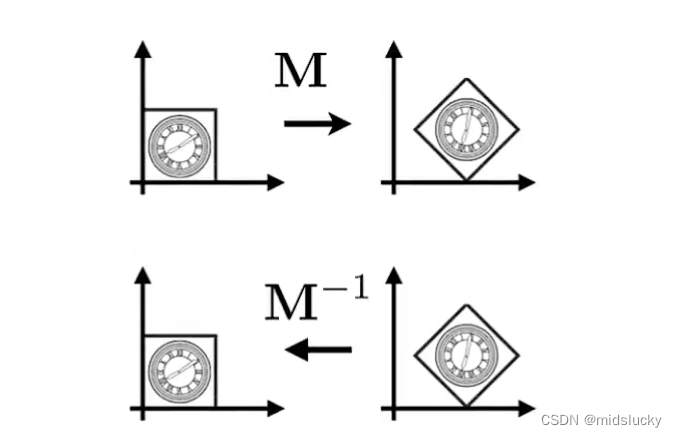
1.6逆变换(Inverse Transform)
2. 3d transformations
2.1 3d空间中点与向量的表达方式

2.2 3d空间当中的旋转
绕轴旋转:
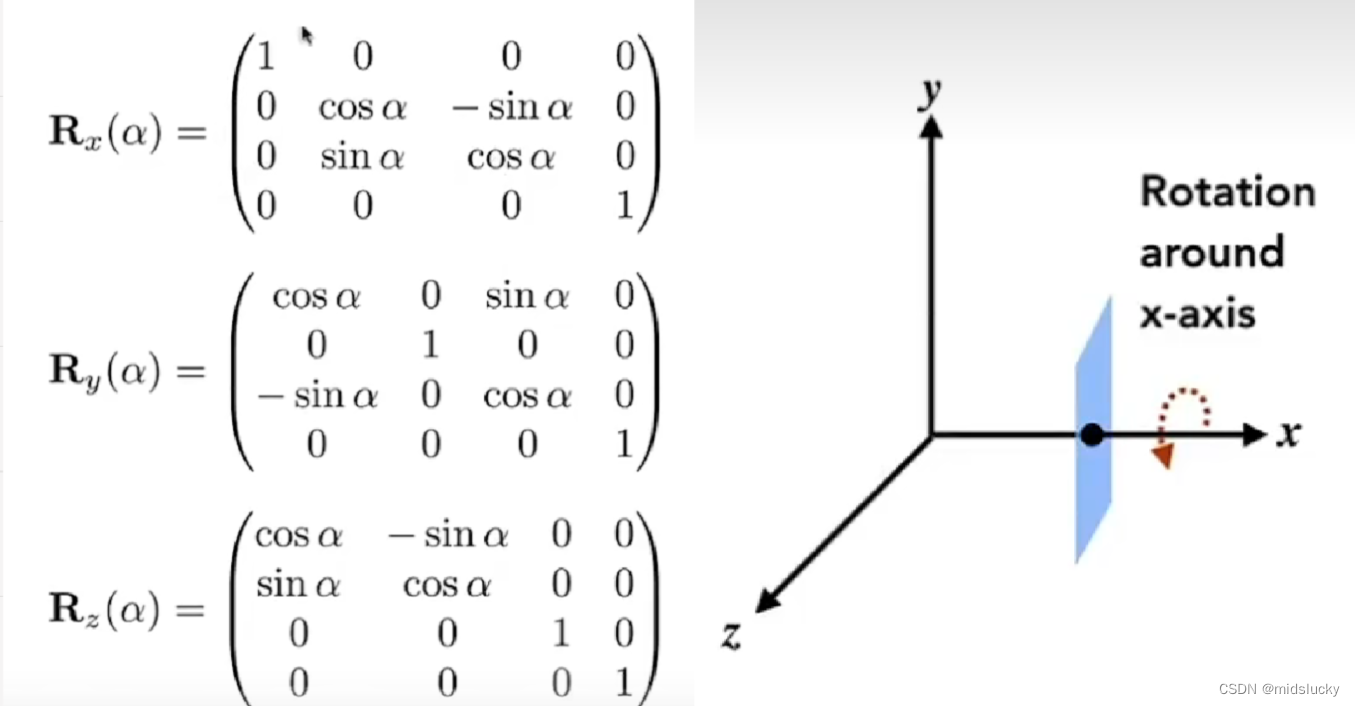
上面的式子分别是一个实际的物体绕着不同轴旋转所对应的线性变换,那么实际应用当中我们是如何处理旋转的呢?
物体实际旋转的处理公式:

实际我们在处理一个物理旋转时,我们会将其拆分为该物体与各个轴之间的旋转变换,我们把如图上的那三个角称作欧拉角。
罗德里格旋转公式(Rodrigues’ rotation formula)
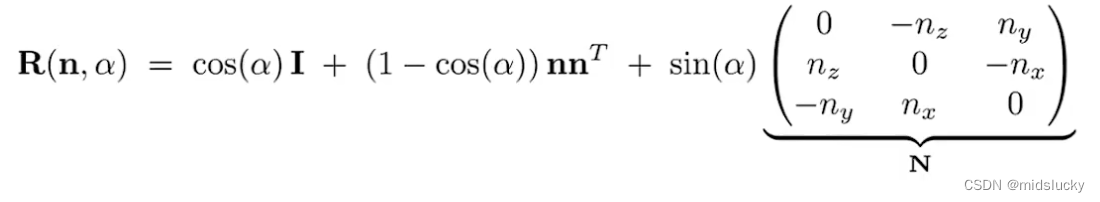
解释一下这个公式的一些参数:n为物体绕着旋转的轴(默认起点为原点,默认旋转方向为逆时针),a为旋转角度。
2.3四元数
最基本的定义:i的二次方 = j的二次方 = -1 且 ij = -ji = k (意味着不满足交换律)
q(四元数) = a + bi + cj + dk 且满足 i的平方 = j的平法 = k的平方 = ijk = -1
这里只展示四元数最基本的定义,后面我会出一篇文章详细讲解一下四元数的实际运用。
3.视图变换(ViewingTransformation)
思考我们拍照的过程:我们的现实是3d坐标系,而我们用相机所拍摄到的照片是二维的,那么如何3d坐标系的影像处理成二维照片呢?这就是我们视图变换所做的事情。
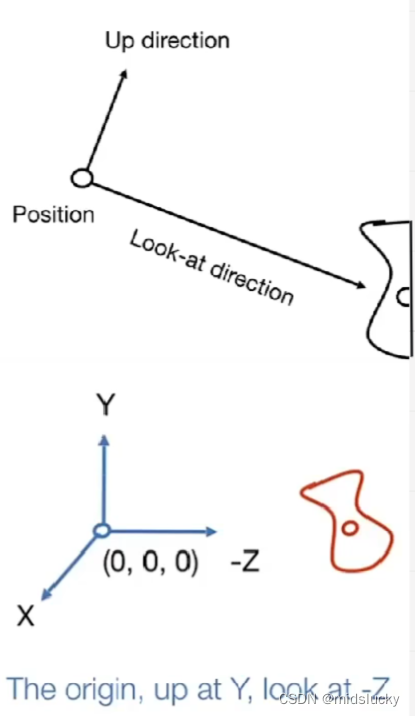
如这副图所示,为了完成我们的变换我们首先得确定相机的位置和确定一个相机的正方向。
当然在我们的实际使用当中我们默认相机固定在原点,y轴为正方向,往-Z轴看。
3.1相机的摆放问题( 摄像机变换(camera tranformation))
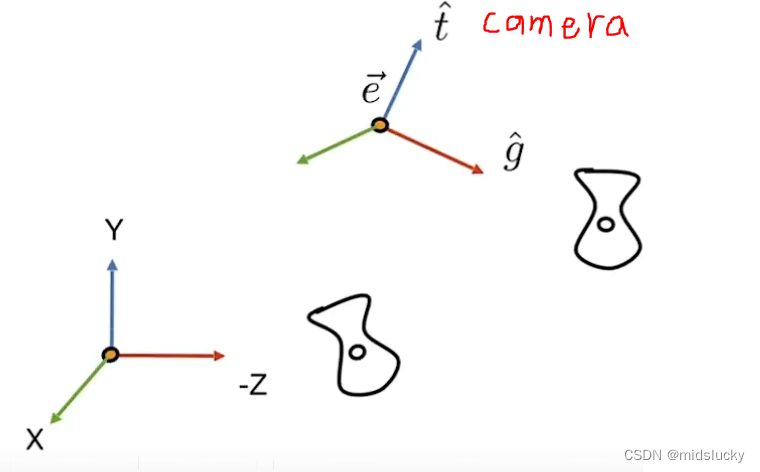
当然我们的相机不可能一直会在原点,就比如如图这样的情况,我们应该如何把相机回归原点呢?(实际上就是把etg坐标系所对应的图像对应到xy-z坐标所对应的图像)
这里可以这么理解:将我们etg坐标系的三个方向进行线性转换变成了xy-z坐标系的三个方向,那么其所对应到的图片经过这样的转换后效果是不变的(不同坐标系与图像的对应关系没有发生变化),这样的过程就好比把计算机从一个随机的位置移动到了原点。
当然我们求etg到对应xy-z这样过程比较困难,不妨先求其逆,也就是xy-z到etg这一线性变换的过程。
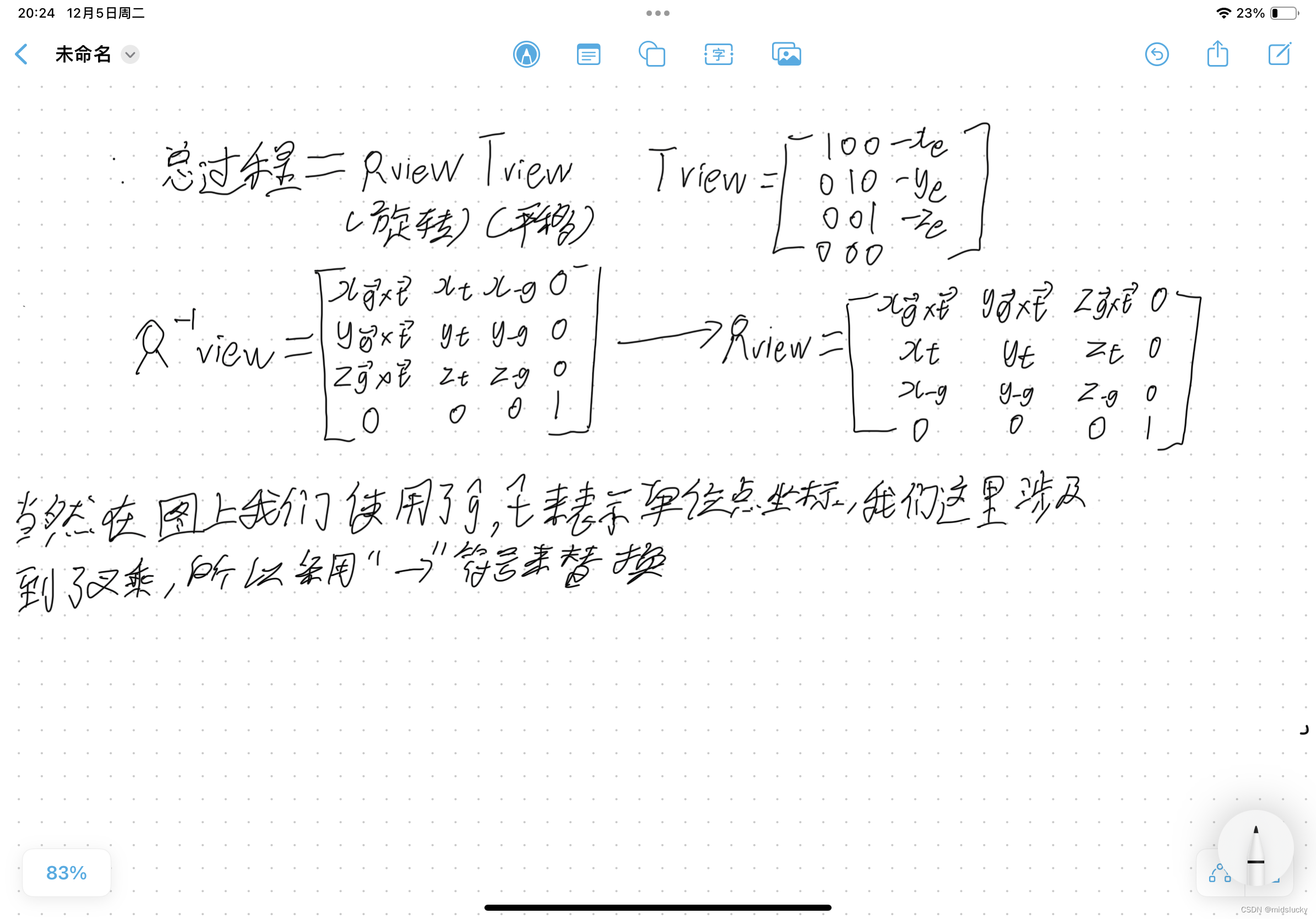
正交矩阵的逆等于其转置矩阵,为什么呢?
这里偷一张大佬的图

3.2 投影变换(projection tranformation)
3.21正交投影(Orthographic projection)
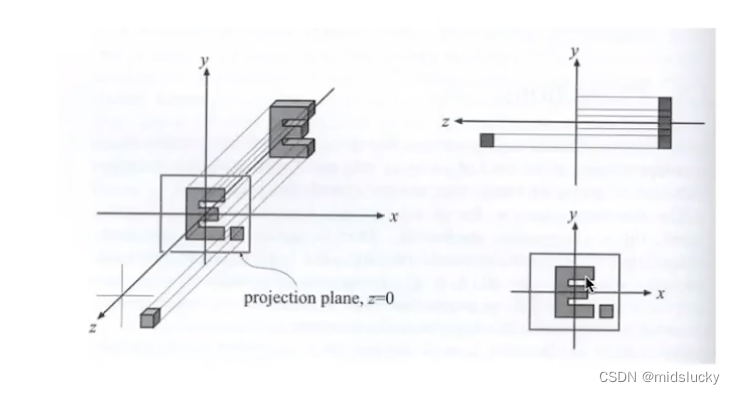
按照视觉效果来说正交投影应该是如上图所示的样子,但是实际处理起来太麻烦,因此我们在实际当中采用如下步骤:

实际上就是先进行了一个平移和一个缩放(缩放成一个边长为2中心在原点的正方形)
3.22透视投影(Perspective projection)
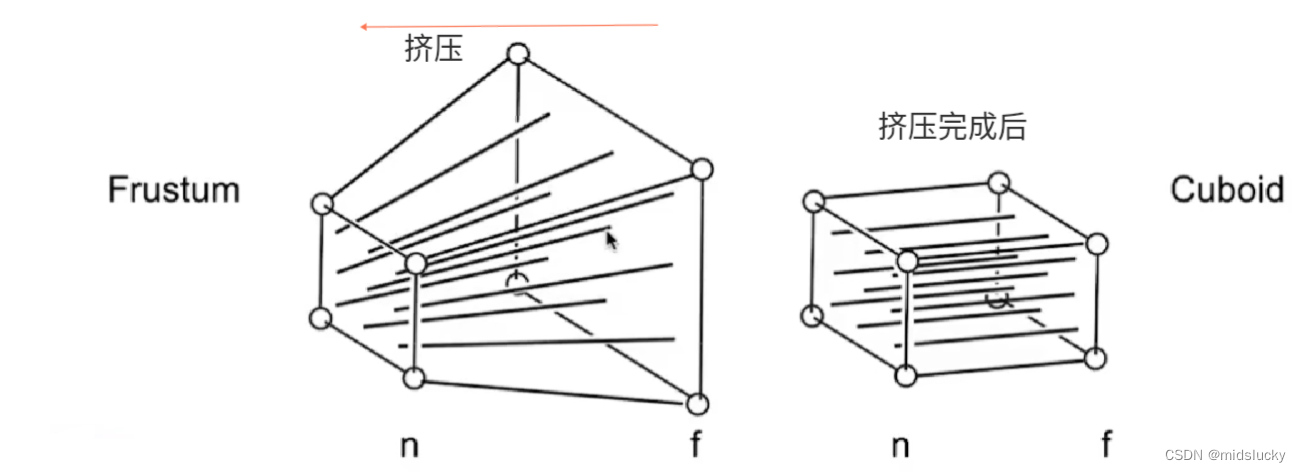
透视投影这一过程其实分为两个部分如上图所示先进行挤压,然后在进行我们上面所说的正交投影来完成这一过程,需要说明的是透视投影在挤压过程中,整个图像上的各个点z坐标是不变的,只是x和y轴上的坐标在发生变化。
那么究竟如何得到这一挤压矩阵呢?不急我们分成了3个步骤。
步骤1
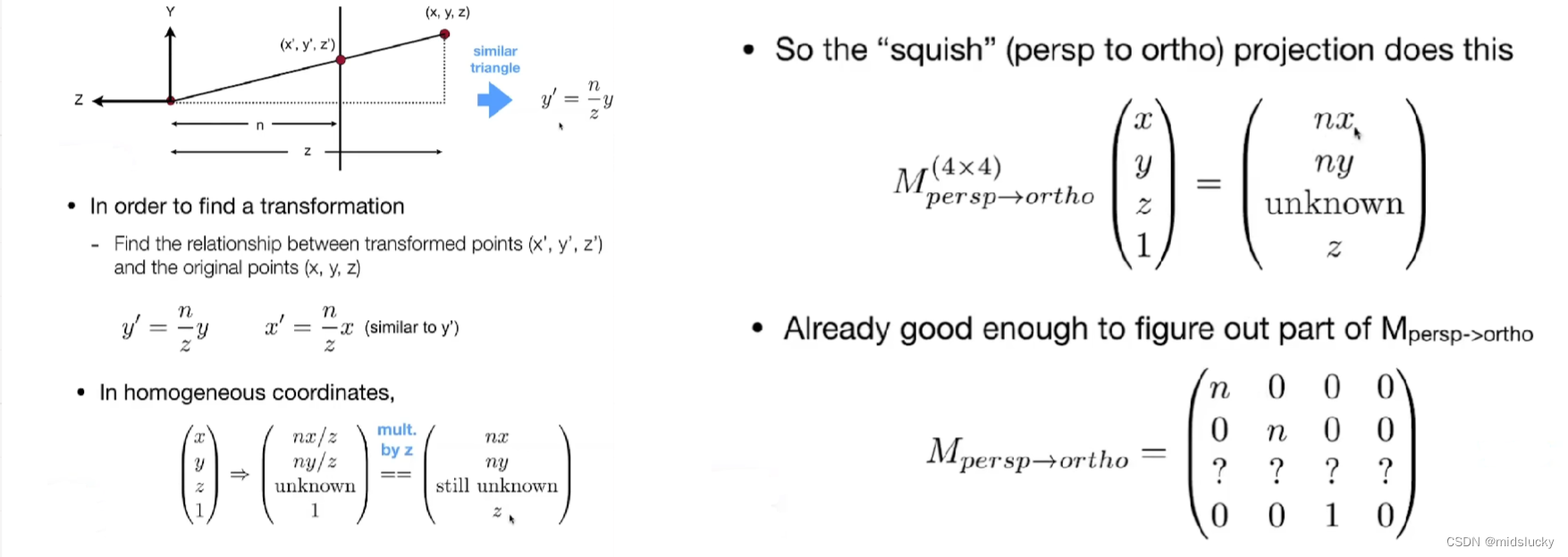
首先在上面我们就强调了每个点的z值不会变化,通过观察我们得到了如上图所示的规律,因此我们可以获得我们的第一个特例,在我们获得的这个特里中乘以z,在通过推导可知,我们能够已知的矩阵信息如右边的矩阵图示。
(这里的乘以z其实两边应该都乘以z等式才能成立,这个乘以z的效果隐藏在那个4乘4矩阵里)
步骤2
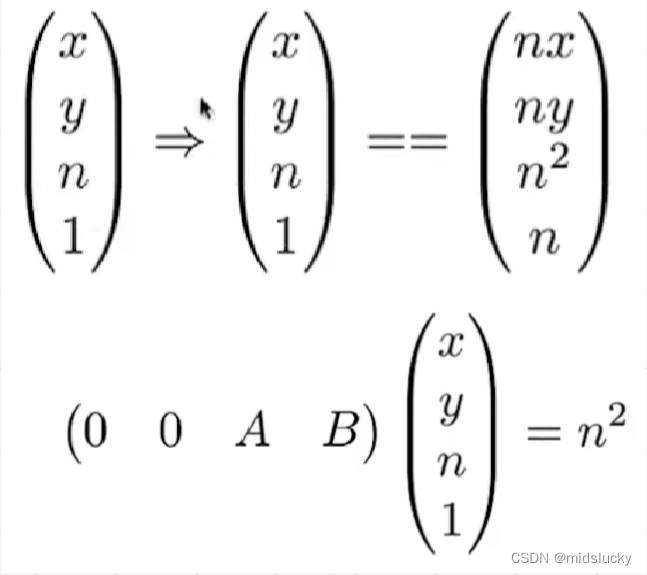
当z等于n时,也就是对应最上面那个挤压图最左边小的那个面,这个时候我们同样在右边乘以z(当然我们这边的z这个常数等于常数n)
步骤三
远处最中心的点在挤压过程中没有改变因此有了如图以下推导:

(tips:中心点的坐标得看坐标系,这里是特意这么设计的)
至此推导结束。