反三角函数

• 反三角函数 (wikipedia.org)

反三角函数图形

$\sin (x),\arcsin (x)$	$\cos (x),\arccos (x)$	$\tan (x),\arctan (x)$
$\arcsin x,\arccos x$	$\arctan x,\mathrm{arccot}x$	$\mathrm{arcsec}x,\mathrm{arccsc}x$

利用反函数的性质绘制反三角图形

• 由于反函数与其原本的直接函数关于$y=x$这一直线对称,因此我们可以根据反三角函数$b(x)$的值域,在直接三角函数上$b(x)$截取一段相应的区间,这部分函数记为$c(x)$
• 再将$c(x)$关于$y=x$作对称图形
• 另一方面结合相关不等式,来提高草图准确度,例如:
  • 由$\sin x<x<\arcsin x$,$(x\in (0,1))$,三条曲线$\sin x,x,\arctan x$在$(0,1)$区间内没有交点,而在$x=0$处三个函数交于原点
  • 又因为三个函数都是奇函数,从而在第三象限三个函数的大小关系相反,且仍然没有交点
  • 也可以结合函数的凹凸性,提高函数图形草图的走势准确度
• 因此绘制反三角函数草图时,先绘制$y=x$,(虚线)然后以其对称轴,绘制直接函数的对称部分

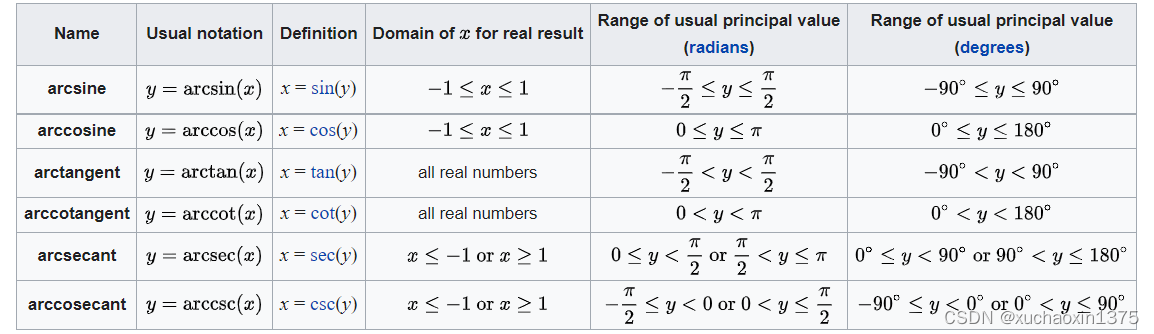
反三角函数的定义域&值域

反三角函数的恒等式

1. $\arcsin x+\arccos x=\frac{\pi }{2}$

2. $\arctan x+\mathrm{arccot}x=\frac{\pi }{2}.$

3. $\arctan x+\arctan \frac{1}{x}=\{\begin{array}{cc}\frac{\pi }{2},& \mathrm{if}x>0\\ -\frac{\pi }{2},& \mathrm{if}x<0\end{array}$

4. $\arctan x+\arctan y=\arctan \frac{x+y}{1-xy}+\{\begin{array}{cc}\pi ,& \mathrm{if}x,y>0\\ -\pi ,& \mathrm{if}x,y<0\\ 0,& \mathrm{otherwise}\end{array}$

5. $\sin (\arccos x)=\sqrt{1-x^2}$

6. $\sin (\arctan x)=\frac{x}{\sqrt{1+x^2}}$

7. $\cos (\arctan x)=\frac{1}{\sqrt{1+x^2}}$

8. $\cos (\arcsin x)=\sqrt{1-x^2}$

9. $\tan (\arcsin x)=\frac{x}{\sqrt{1-x^2}}$

10. $\tan (\arccos x)=\frac{\sqrt{1-x^2}}{x}$

推导

以第一个$\arcsin x+\arccos x=\frac{\pi }{2}$为例

• 由于$\cos \theta =\sin (\frac{\pi }{2}-\theta )$,设它们都等于$x$.则得到$\cos \theta =x$(1);$\sin (\frac{\pi }{2}-\theta )=x$(2)
  • 对(1)两边同时取$\arcsin$,得$\theta =\arcsin x$;$\frac{\pi }{2}-\theta =\arccos x$,两式相加,得$\arcsin x+\arccos x=\frac{\pi }{2}$

以第一个$\arctan x+\mathrm{arccot}x=\frac{\pi }{2}$也是类似的

• 由于$\tan (\frac{\pi }{2}-\theta )$=$\cot \theta$,可令$\tan (\frac{\pi }{2}-\theta )$=$x$;$\cot \theta =x$
• 所以$\frac{\pi }{2}-\theta =\arctan x$;$\theta =\mathrm{arccot}\theta$
• 两式相加,得$\arctan x+\mathrm{arccot}x=\frac{\pi }{2}$