题目及要求

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:

输入: numRows = 1
输出: [[1]]

提示:

1 <= numRows <= 30

动态规划

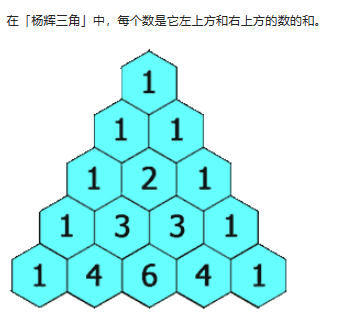
很经典的题目，杨辉三角的特性为：
1、第一行只有一个数1。
2、除了每行的第一个数和最后一个数是1以外，任意其他位置的数，都是它正上方的数和左上方的数之和。
3、第n行（行号从0开始）有n+1个数。
初始化第一行和第二行
对于第三行及之后的每一行，根据杨辉三角的规则计算：
每行的第一个元素是1，使用 emplace_back 添加到当前行。
接着计算中间的元素，这些元素等于它正上方的元素和左上方的元素之和，即 dp[i-1][j] + dp[i-1][j-1]。
每行的最后一个元素也是1，同样使用 emplace_back 添加到当前行。

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>>dp(numRows);
        if(numRows>=1)dp[0].emplace_back(1);
        if(numRows>=2){
            dp[1].emplace_back(1);   //初始化第二行都为1
            dp[1].emplace_back(1);
        }
        for(int i=2;i<numRows;i++){
            dp[i].emplace_back(1);
            for(int j=1;j<=i-1;j++){
                dp[i].emplace_back(dp[i-1][j]+dp[i-1][j-1]);
            }
            dp[i].emplace_back(1);
        }
        return dp;
    }
};

在mian内使用

int main() {
    int numRows = 5; // 设置 numRows 想生成的杨辉三角的行数
    Solution solution;
    vector<vector<int>> result = solution.generate(numRows);

    // 打印杨辉三角
    for (const auto& row : result) {
        for (int num : row) {
            cout << num << " ";
        }
        cout << endl;
    }

    return 0;
}