这里写目录标题
- xmind
- 单源最短路
- 简介
- 所有边权都是正
- 朴素的Dijkstra算法
- 思想
- 例子+题解
- 堆优化版的Dijkstra算法
- 存在负数权
- Bellman-Ford算法
- 思想
- 例子+题解
- 多源汇最短路
- 简介
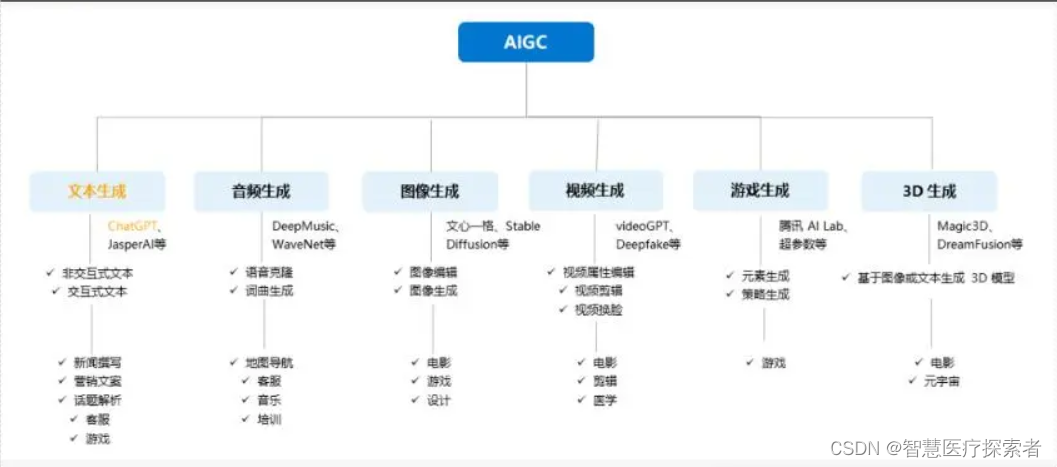
xmind

上述中,朴素Dijkstra算法适用于稠密图
其他用堆优化版
而SPFA算法一般都比Bellman-Ford算法要快
Floyd没得选
稠密图和稀疏图的定义:

其中m是边数,n是点数
当m的数据量与n方一样或者更多,那么就是稠密图,如果m跟n数据量一样,或者说更少,那么就是稀疏图

最短路问题,只会考察如何抽象出问题并实现代码,并不会考察算法的原理,重点在于抽象以及代码的实现
单源最短路
简介
只有一个起点,到其他某个点的最短路
所有边权都是正
朴素的Dijkstra算法
思想

一些解释:
s数组存放目前已经确定的最短距离的点
第一步中:dis数组是某个点到原点的距离,初始化一号点(一号点就是源点,因为图论中结点的编号都是从1开始的)的dis数值为0,其他全为一个很大的数
第二步中:for 遍历i从0到n
对于每次循环
将不在s中的距离dis最近的点给到t
把t加到s
用t来更新其他所有点的距离,如上图,如果满足dis[x]>dis[t]+w(t到x的权值),那么更新dis[x]的值为dis[t]+w的值
因为该算法适用于稠密图,所以用邻接矩阵来存储图
例子+题解



数据分析:n m分别是点数和边数
g数组存放某两个点的权值,例如g[a][b]=1,表示a与b之间的权值是1
dist数组用来存放某个点到原点也就是一号点的距离
st数组就是用来表示某个点的最短路已经被找到
dijkstra算法:
首先初始化dist为无穷大,用十六进制0x3f初始化即可
之后初始化dist[1]为0,因为一号点是源点
之后for循环,循环n次
首先初始化t为-1
之后,对于每个节点编号从1到n
if(某个点没有确定最短路,并且(t未被赋值,或者,j是没有确定最短路的最近的点即dist[t]>dist[j]) ),这时将j赋值给t
同时更新st[t]为true
然后对每个节点编号进行循环,用t更新其他结点的最短路
dist[j]=min(dist[j],dist[t]+g[t][j])
最后,如果dist某个点的距离仍然是0x3f(因为利用memset初始化是初始其值的三分之一即可,但是0,-1是初始化自己),那么返回-1,表示路径不存在
最后返回dist[n],这里根据具体的题目要求进行返回即可,因为题目让返回n号点

之所以取min,是因为该题存在自环和重边,如下:但是因为要求最短路,所以当某两个点有多个权值的时候,取权值最小的当做其权值,较大的权值就不看了

堆优化版的Dijkstra算法
题目与上面的题一样

对于add算法:
idx表示当前e数组中的可用位置,将目标点的编号存入e[]数组中,并且用一个w数组来维护权值,同时头插法:ne[idx]=h[a],h[a]=idx++
(因为e数组就是用来存节点信息的,又因为e数组所存信息的结点都是一个节点的出边节点组成的链表,所以信息就是节点的编号,所以目标结点的编号都放在e[]数组里,发出结点的编号都在h数组,所以函数里都是h[a])

首先是一个优先队列,其中第二第三个参数是用来改变默认排序,改成从大到小排列
用一个pari来维护一个结点编号以及该点到源点的距离
while循环条件队列不空
然后取出队头元素给到t(没有确定最短路径的点,且距离源点最近)
之后将队头元素出队
然后拿到t的编号以及到源点的距离
if(st[ver]是真),那么说明这是重边,countinue即可
之后,用t来更新其他结点的最短路径:
for循环中,遍历t结点的所有一级出边,对于每个子链结点,拿到其存在e数组中的编号之后给j
之后更新
之后出队j的pair:{dist[j],j}

存在负数权
Bellman-Ford算法
思想

上面的方框是算法过程,下面的圆是经过该算法之后出现的现象,即对于每个a,b:dist[b]<=dist[a]+w,俗称三角不等式

其中 第一个for循环的次数是有实际意义的,循环k次,表示最短路径最多经过不超过k条边到达目标点

例子+题解

输出案例:3

数据分析:
backup数组是用来备份dist数组的
结构体用来存放某两个点以及两个点之间的距离
并用该结构体类型创建边数组
对于bellman-ford算法
首先初始化dist数组
之后因为题目要求最多不超过k条边,所以循环k次
在k次循环的每次循环时,首先备份dist到backup数组
然后对于m条边,有m次循环,因为结构体来存放边,每个边是一个结构体元素,所以有几个边,就循环几次
之后利用结构体数组拿到每个边的数据,利用备份的a来更新dist[b]
最后如果n点(具体哪个点看题目要求)的dist>0x3f3f3f/2(记住就好),那么就表示没有最短路径
最后返回dist[n]

对于为什么要备份,如下:

因为有k条边的限制,所以,不能向之前那样,一个接着一个更新,这样的话,就会无视k条边的限制,直接找到没有限制的最短路径

利用备份的数据进行更新,每次都是最初版本的数据,都是正无穷,所以,不会发生数据更新,就会被限制到
多源汇最短路
简介
多个起点