背景：
  2000年5月24日，新罕布什尔州的克莱数学研究所列出了数学和计算机科学中七个未解决的问题。然而，直到今天，这些问题中只有一个被解决了，那就是庞加莱猜想（Poincaré Conjecture）——被俄罗斯数学家格里戈里-佩雷尔曼解决。而 P vs NP 问题就是其他六个未解决的问题之一。

算法时间复杂度排序：

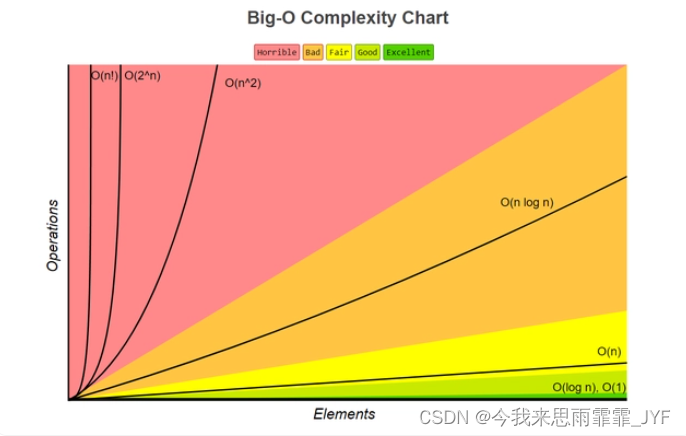
$O(1)<O(\log n)<O(n)<O(n\log n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$

其中，$O(1)<O(\log n)<O(n)<O(n\log n)<O(n^2)<O(n^3)$ 为多项式算法复杂度，$O(2^n)<O(n!)<O(n^n)$ 为非多项式算法复杂度。

P问题：

  就是可以在多项式时间内解决的问题；一个规模为 n 的问题，如果能在 n 的多项式时间内解决，就是 p 问题。

NP问题：

  是指可以在多项式的时间里验证一个解的问题。

NP-Hard问题：

  若所有的 NP 问题都能在多项式时间内归约（转化）到问题 X（原$NP{\le }_{p}X$）。则 X 为 NP-Hard 问题。

NP-complete问题：

  如果 $X\in NP$ 并且 X 是 NP-Hard 问题，则 X 是 NP-complete 问题。例如逻辑电路（给定一个逻辑电路，问是否存在一种输入使输出为 True）、Hamilton 回路问题、旅行商问题等。

 
 
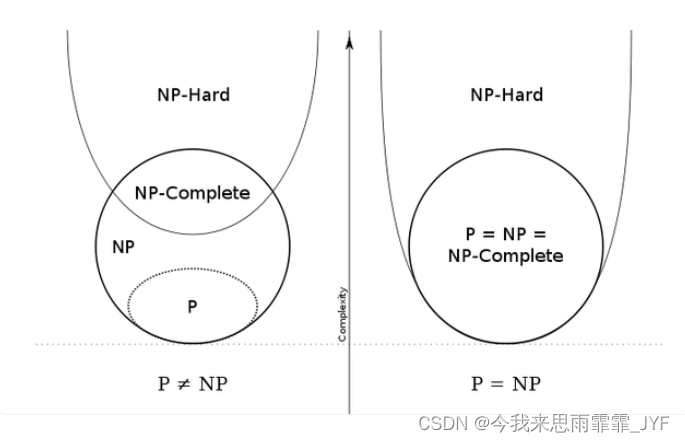
致谢：【谈谈计算机中的NP，NP-Hard，NP完全以及"NP=P？"问题】 https://www.bilibili.com/video/BV1Wz4y1d7wb/?share_source=copy_web&vd_source=9a6c606c6f9df7c015effdcaa7e1fa84
   https://baijiahao.baidu.com/s?id=1713392916192844115&wfr=spider&for=pc