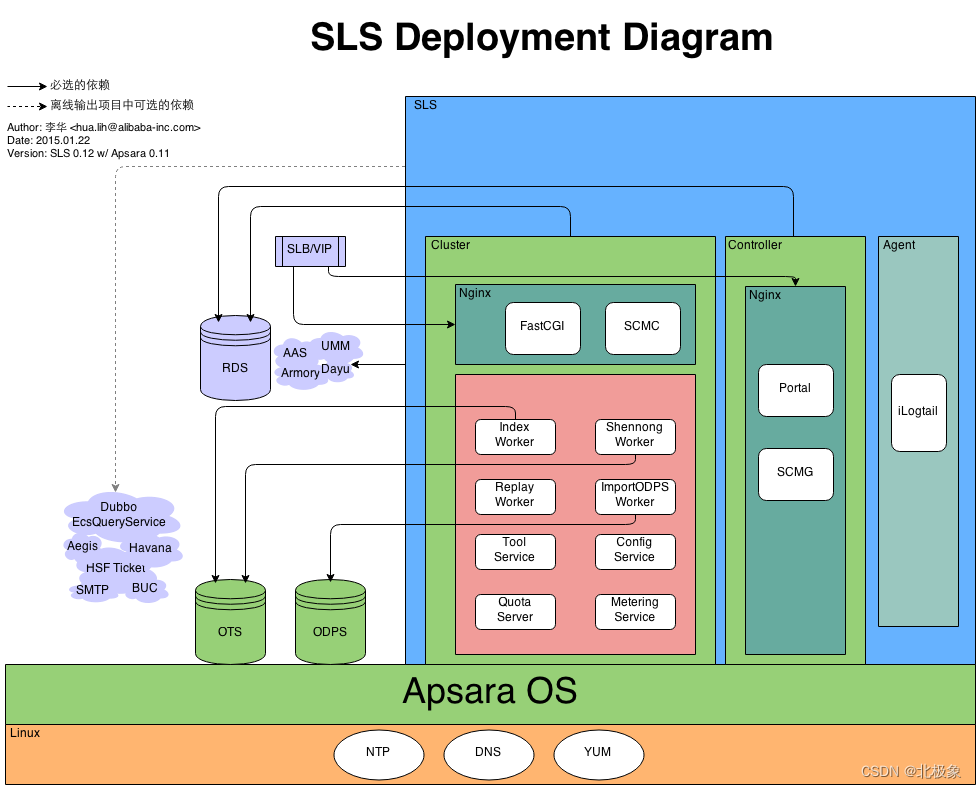
过程化处理中希望能够对某块区域生成随机多边形，以及再切割成子多边形
各种尝试之后发现一种通过python、turtle、pyclipper实现的简单方案

随机多边形

采用python直接生成随机多边形，算法原理：将360度随机拆分成各个角度，再通过随机半径连接起来

def get_random_poly(num_vertices, bounds):
    radii=[]
    for i in range(num_vertices):
        radii.append(random.uniform(0.5,1.0))
    min_weight=1.0
    max_weight=10.0
    total_weight=0.0
    angle_weights=[]
    for i in range(num_vertices):
        angle_weights.append(random.uniform(min_weight,max_weight))
        total_weight+=angle_weights[-1]
    angles=[]
    for angle_weight in angle_weights:
        angles.append(angle_weight*2*math.pi/total_weight)
    rx=(bounds[1][0]-bounds[0][0])/2
    ry=(bounds[1][1]-bounds[0][1])/2
    cx=bounds[0][0]+rx
    cy=bounds[0][1]+ry
    points=[]
    theta=0.0
    for i in range(num_vertices):
        points.append((
            cx+rx*radii[i]*math.cos(theta),
            cy+ry*radii[i]*math.sin(theta)))
        theta+=angles[i]
    return points

生成用以拆分多边形的矩形

采用中心点、法线矢量的方式生成

def get_perpendicular_rect(c,pn,hl,hw):
    p0=(c[0]+pn[1]*hl,c[1]-pn[0]*hl)
    p1=(c[0]-pn[1]*hl,c[1]+pn[0]*hl)
    rect=[]
    rect.append((p0[0]+pn[0]*hw,p0[1]+pn[1]*hw))
    rect.append((p0[0]-pn[0]*hw,p0[1]-pn[1]*hw))
    rect.append((p1[0]-pn[0]*hw,p1[1]-pn[1]*hw))
    rect.append((p1[0]+pn[0]*hw,p1[1]+pn[1]*hw))
    return rect

拆分多边形

采用pyclipper库实现任意多边形拆分，算法原型是Vatti clipping
这里采用递归的方式分割子多边形，直到面积小于指定值

import turtle
import random
import math
import pyclipper
...
# 计算多边形中心点
def get_poly_center(poly):
    c=[0,0]
    for p in poly:
        c[0]+=p[0]
        c[1]+=p[1]
    c[0]/=len(poly)
    c[1]/=len(poly)
    return c
    
# 计算两点距离的sqrt
def get_distsq(p0,p1):
    d=(p1[0]-p0[0],p1[1]-p0[1])
    return d[0]*d[0]+d[1]*d[1]
    
# 获取多边形中最远的点
def get_furthest_point(poly):
    c=get_poly_center(poly)
    f=poly[0]
    sq=get_distsq(c,f)
    for i in range(1,len(poly)):
        sq2=get_distsq(c,poly[i])
        if sq2>sq:
            sq=sq2
            f=poly[i]
    return c,f

# 计算多边形面积，正负可用来判定多边形矢量方向
def get_poly_area(poly):
    area=0
    v0=poly[0]
    v1=poly[1]
    for i in range(2,len(poly)):
        v2=poly[i]
        area+=(v1[0]-v0[0])*(v2[1]-v0[1])-(v1[1]-v0[1])*(v2[0]-v0[0])
        v1=v2
    return area*0.5

# 递归分割多边形，maxarea为最小不可分割面积
def clip_poly(poly,hl,hw,maxarea):
    ret=[]
    c,f=get_furthest_point(poly)
    d=[f[0]-c[0],f[1]-c[1]]
    l=math.sqrt(d[0]*d[0]+d[1]*d[1])
    d[0]/=l
    d[1]/=l
    pc=pyclipper.Pyclipper()
    pc.AddPath(poly,pyclipper.PT_SUBJECT,True)
    pc.AddPath(get_perpendicular_rect(c,d,hl,hw),pyclipper.PT_CLIP,True)
    for r in pc.Execute(pyclipper.CT_DIFFERENCE,pyclipper.PFT_EVENODD,pyclipper.PFT_EVENODD):
        area=get_poly_area(r)
        if area>=0:
            r.reverse()
        if math.fabs(area)<=maxarea:
            ret.append(r)
        else:
            reg=clip_poly(r,hl,hw,maxarea)
            for r2 in reg:
                ret.append(r2)
    return ret

通过turtle工具将切割效果显示出来

这里要注意turtle坐标中心点位于画布中央，x轴正向朝右，y轴正向朝上

...
# 利用鼠标点击事件可多次查看分割效果
def onmouseclick(x,y):
    radius=100
    poly=get_random_poly(10, ((x-radius,y-radius),(x+radius,y+radius)))
    reg=clip_poly(poly,900,3,300)
    for poly in reg:
        poly.append(poly[0])
        for p in poly:
            turtle.goto(p)
            turtle.down()
        turtle.up()

# python主程序入口
if __name__=='__main__':
    ts=turtle.getscreen()
    ts.onclick(onmouseclick)
    turtle.up()
    # 设置随机种子用以固定每次生成的结果
    random.seed(3)
    onmouseclick(0,0)
    turtle.done()

最终效果

参考

https://blog.csdn.net/bby1987/article/details/108858785
https://blog.csdn.net/qq_25737169/article/details/113843872
https://blog.csdn.net/ithiker/article/details/127712621