nn.Module（模组）

nn.Linear是线性层

torch.optim (优化)

这是一个实现各种优化算法的包。

在调用的时候将需要优化的参数传人，这些参数都必须是Variable, 然后传入一些基本的设定，比如学习率和动量等。

举个例子：

optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

看到这里，如果代码不太懂的可能有点懵，不过深度学习的代码就是这样，分几个层次来构建一个完整的模型。

模型的保存和加载

两种方式，各有各的不同之处。

一维线性回归

深度学习的一层神经网络呗（粗略地这样认为是可以的）
至于总的线性模型的式子其实其他教程上都有：

在代码实现的过程中我又又报错了，然后我心平气和地去找改错的博文，thistorch踩坑

改完错误的我，真的是高兴呢！，书中作者的代码不知道是哪年的，自己敲的时候没报错，我敲的时候就报错了，根据报错信息来看，应该是版本不一样导致的语法修改。

%notebook的魔法命令

代码如下：

import torch
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import torch.nn as nn

x_train = np.array([[3.3],[4.4], [5.5], [6.71], [6.93], [4.168],
[9.779],[6.182], [7.59], [2.167], [7.042] ,
[10.791],[5.313], [7.997], [3.1]], dtype=np.float32)

y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
[3.366], [2.596], [2.53], [1.221], [2.827],
[3.465],[1.65], [2.904], [1.3]], dtype=np.float32)

plt.scatter(x_train, y_train)
plt.show()

#转化成张量Tensor，否则没法用库函数,这一步也就是把数据准备好
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)

#构造线性模型
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression,self).__init__()
        self.linear = nn.Linear(1,1) # input and output is 1 dimension
    def forward(self, x) :
        out = self.linear(x)
        return out
if torch.cuda.is_available() :
    model = LinearRegression().cuda()
else:
    model=LinearRegression() 

LinearRegression(
  (linear): Linear(in_features=1, out_features=1, bias=True)
)

# 定义损失函数和优化函数
#这里使用梯度下降
criterion = nn.MSELoss() #在这里定义的损失函数，然后可以把criterion当作函数来使用，相当于C++的函数指针 了
optimizer = torch.optim.SGD(model.parameters(),lr=1e-3) # 与上句同理

from torch.autograd import Variable # torch 中 Variable 模块

num_epochs = 1000
for epoch in range(num_epochs) :
    if torch.cuda.is_available() :
        inputs = Variable(x_train).cuda()
        target = Variable(y_train).cuda()
    else:
        inputs = Variable(x_train)
        target = Variable(y_train)
        
    # forward
    out = model(inputs) # 将输入的数值输入到线性模型中进行计算，计算完的输出保存在out变量中。在class LinearRegression(nn.Module)中最后return的也是out
    loss = criterion(out, target) # 计算损失
    
    # backward
    optimizer.zero_grad() # 清空过往梯度
    loss.backward() # 反向传播，计算当前梯度
    optimizer.step() # 根据梯度更新网络参数
    
    if (epoch+1)%20 == 0: # 网络上很炫的训练过程可视化就是这样朴实无华
        print('Epoch[{}/{}], loss: {:.6f}'.format(epoch+1, num_epochs, loss.data))

Epoch[20/1000], loss: 0.376377
Epoch[40/1000], loss: 0.374250
Epoch[60/1000], loss: 0.372151
Epoch[80/1000], loss: 0.370074
Epoch[100/1000], loss: 0.368018
Epoch[120/1000], loss: 0.365983
Epoch[140/1000], loss: 0.363968
Epoch[160/1000], loss: 0.361975
Epoch[180/1000], loss: 0.360001
Epoch[200/1000], loss: 0.358048
Epoch[220/1000], loss: 0.356115
Epoch[240/1000], loss: 0.354201
Epoch[260/1000], loss: 0.352307
Epoch[280/1000], loss: 0.350433
Epoch[300/1000], loss: 0.348578
Epoch[320/1000], loss: 0.346741
Epoch[340/1000], loss: 0.344924
Epoch[360/1000], loss: 0.343124
Epoch[380/1000], loss: 0.341344
Epoch[400/1000], loss: 0.339581
Epoch[420/1000], loss: 0.337837
Epoch[440/1000], loss: 0.336110
Epoch[460/1000], loss: 0.334401
Epoch[480/1000], loss: 0.332710
Epoch[500/1000], loss: 0.331035
Epoch[520/1000], loss: 0.329378
Epoch[540/1000], loss: 0.327738
Epoch[560/1000], loss: 0.326115
Epoch[580/1000], loss: 0.324508
Epoch[600/1000], loss: 0.322917
Epoch[620/1000], loss: 0.321343
Epoch[640/1000], loss: 0.319785
Epoch[660/1000], loss: 0.318243
Epoch[680/1000], loss: 0.316717
Epoch[700/1000], loss: 0.315206
Epoch[720/1000], loss: 0.313711
Epoch[740/1000], loss: 0.312231
Epoch[760/1000], loss: 0.310766
Epoch[780/1000], loss: 0.309316
Epoch[800/1000], loss: 0.307881
Epoch[820/1000], loss: 0.306460
Epoch[840/1000], loss: 0.305054
Epoch[860/1000], loss: 0.303663
Epoch[880/1000], loss: 0.302286
Epoch[900/1000], loss: 0.300922
Epoch[920/1000], loss: 0.299573
Epoch[940/1000], loss: 0.298237
Epoch[960/1000], loss: 0.296916
Epoch[980/1000], loss: 0.295607
Epoch[1000/1000], loss: 0.294312

# 训练完就该预测了（这里就是一维线性模型,很简单,没啥其他的步骤）
%matplotlib notebook

model.eval()
model.cpu() # 修改为CPU调用
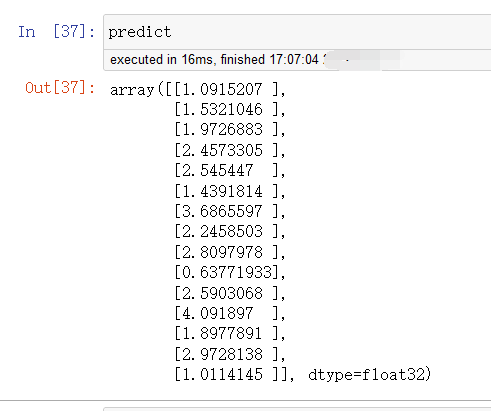
predict = model(Variable(x_train))  #调用训练好的模型，然后将模型的输出用predict保存
predict = predict.data.numpy()

#看一下拟合效果
plt.plot(x_train.numpy(), y_train.numpy(),'ro', label='Original data')
plt.plot(x_train.numpy(), predict, label='Fitting Line')
plt.show()

<IPython.core.display.Javascript object>

大家注意看我的代码都是由哪几部分组成的，构建深度学习项目其实就是大概的几部分了。

然后咱们要学精，得看一看这些语法有没有可以深究的。

首先就是导入包，为了避免语法错误最好一开始就导入。

均方差损失函数nn.MSELoss()

nn.MSELoss()，当输入两个矩阵时，默认输出标量tensor（torch.Size([])），是两个矩阵对应位置平方差后的平均值

model.parameters()的理解与使用

model.parameters()保存的是Weights和Bais参数的值。

torch.autograd.Variable

是Autograd的核心类，它封装了Tensor，并整合了反向传播的相关实现(tensor变成variable之后才能进行反向传播求梯度?用变量.backward()进行反向传播之后,var.grad中保存了var的梯度)

Varibale包含三个属性：

data：存储了Tensor，是本体的数据
grad：保存了data的梯度，本事是个Variable而非Tensor，与data形状一致
grad_fn：指向Function对象，用于反向传播的梯度计算之用

optimizer.zero_grad()

传统的训练函数，一个batch是这么训练的：
简单的说就是进来一个batch的数据，计算一次梯度，更新一次网络

model.eval的作用

训练完train_datasets之后，model要来测试样本了。在model(test_datasets)之前，需要加上

model.eval()

否则的话，有输入数据，即使不训练，它也会改变权值。
这是model中含有batch normalization层所带来的的性质。
在做one classification的时候，训练集和测试集的样本分布是不一样的，尤其需要注意这一点。

深度学习方法——pytorch下GPU与CPU调用的切换

这篇博文值得一看

看一下各个变量

#访问模型和优化器
print('模型的sate_dict:')
print(model.state_dict().keys())
for param_tensor in model.state_dict():
  print(param_tensor,'\t',model.state_dict()[param_tensor].size())
print('优化器的state_dict：')
for var in optimizer.state_dict():
  print(var,'\t',optimizer.state_dict()[var])



#保存和加载模型
path='model.pt'
torch.save(model.state_dict(),path)

model2=LinearRegression()
#加载
device=torch.device('cpu')#在cpu上保存
# device=torch.device('cuda')#在GPU上保存

model2.load_state_dict(torch.load(path,map_location=device))