插值和拟合的区别（了解）

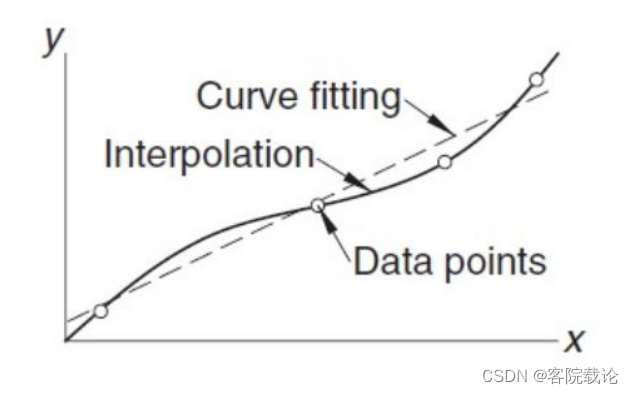
• 插值：是曲线，其中f（x）=y，每一个点都是严格等于的。
• 拟合：是直线，f（x）≈y，大部分的点都在函数值的附近。

拉格朗日插值（必考）

• 公式定义：
  

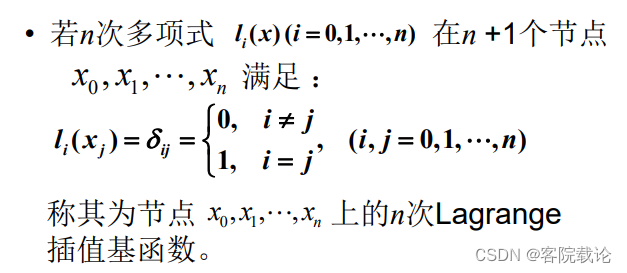
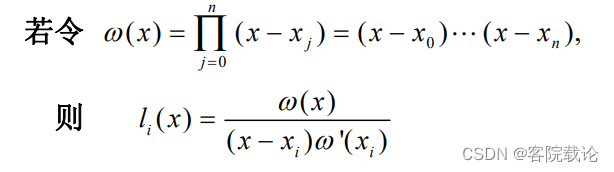
• 记忆
  

• 考核方式能够写出写出对应的插值公式
  

插值余项

• 求导的次数为插值的项数

说不定会考的证明题

• 证明拉格朗日插值公式中的每一项可以构成n次多项式空间的一组基，个数相等，只需要证明其是线性无关的。
  

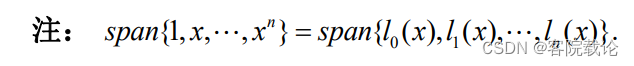
拉格朗日插值缺点和适用范围（了解）

• 注意：无继承性会考，这个基本特点要记住

牛顿插值（必考）

推导

差商的性质（会考）——通过导数来计算差商

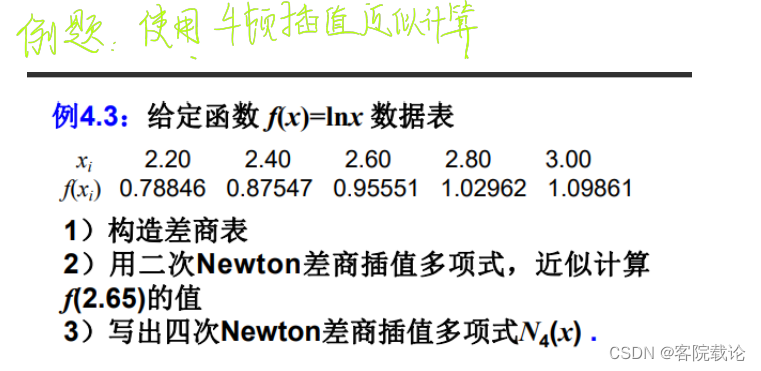
例题计算

埃尔米特插值（必考）

推导

• 注意
  • 插值数据是从低阶到高阶的方式给出的，先有原来的数据，才有一阶导，然后才有二阶导
  • 多重根方程的书写，是二次的

使用埃尔米特插值解决问题的方式

• 问题
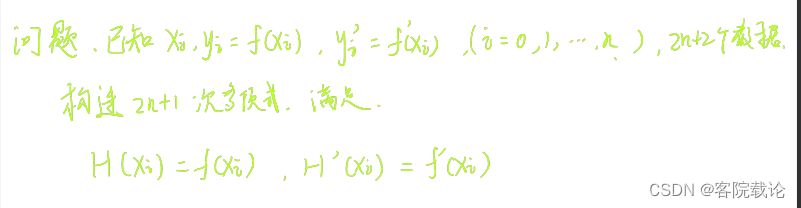
• 解答（使用拉格朗日的解答方式）
  

第一个大题（考试必考，并且就是按照这种方式综合所学插值公式）

• 要求
  • 能够根据给出的插值条件（一定包含若干导数），写出对应的插值公式
  • 能够根据的方程写出对应的插值余项
• 例题
  
• 解决方法
  
  

总结

• 插值是第一个答题，能够根据插值条件写出插值公式即可。
• 后续的样条插值和分段线性插值，不考，全做了解即可