引言

上一节介绍了MCMC以及平均场理论变分推断方法的弊端并介绍了醒眠算法(Weak-Sleep Algorithm)。本节将介绍从KL散度(KL Divergence)角度观察醒眠算法的两个迭代步骤。

回顾： 醒眠算法过程

这里以一个比较简单的$\text{Sigmoid}$信念网络概率图结构为例：

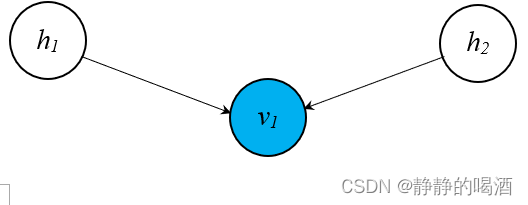
醒眠算法包括两个步骤：

• $\text{Weak Phase :}$ 其本质上是通过采样的方式得到一个关于$\mathcal{P}(h\mid v)$的近似后验。以某具体样本$v^{(i)}=v_1^{(i)}$为例，它关于隐变量的后验概率分布表示如下：
  这里的示例比较简单，样本中仅包含一个随机变量。
  $$\mathcal{P}(h^{(i)}\mid v^{(i)})=\mathcal{P}(h_1^{(i)},h_2^{(i)}\mid v_1^{(i)})$$
  这明显是关于$h_1^{(i)},h_2^{(i)}$的 联合后验分布——那么$\text{Weak Phase}$是如何实现近似后验的呢？$\text{Weak Phase}$具体过程表示如下(红色线)：
  
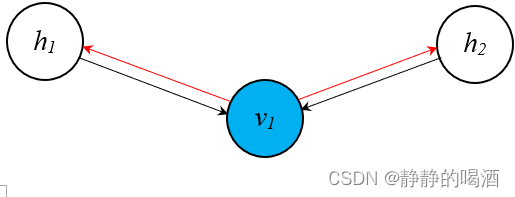
  以具体样本$v^{(i)}=v_1^{(i)}$为基础，对隐变量的后验进行采样。根据概率图模型——贝叶斯网络结构表示红色线部分明显是一个同父结构(Common Parent)。因而在给定(可观测)$v_1^{(i)}$的条件下，$h_1^{(i)},h_2^{(i)}$之间相互独立：
  $$\mathcal{P}(h_1^{(i)},h_2^{(i)}\mid v_1^{(i)})=\mathcal{P}(h_1^{(i)}\mid v_1^{(i)})\cdot \mathcal{P}(h_2^{(i)}\mid v_1^{(i)})$$
  $h_1^{(i)},h_2^{(i)}$各自的后验概率分布分别表示为：
  这里用$\mathcal{R}$替代上一节的$r$，更容易分辨些~
  $$\begin{gathered} \mathcal{P}(h_1^{(i)}\mid v_1^{(i)})=\{\begin{array}{l}\sigma \left({\mathcal{R}}_{v_1^{(i)}\to h_1^{(i)}}\cdot v_1^{(i)}\right)h_1^{(i)}=1\\ 1-\sigma \left({\mathcal{R}}_{v_1^{(i)}\to h_1^{(i)}}\cdot v_1^{(i)}\right)h_1^{(i)}=0\end{array} \\ \mathcal{P}(h_2^{(i)}\mid v_1^{(i)})=\{\begin{array}{l}\sigma \left({\mathcal{R}}_{v_1^{(i)}\to h_2^{(i)}}\cdot v_1^{(i)}\right)h_2^{(i)}=1\\ 1-\sigma \left({\mathcal{R}}_{v_1^{(i)}\to h_2^{(i)}}\cdot v_1^{(i)}\right)h_2^{(i)}=0\end{array} \end{gathered}$$
  至此，已经求出$\mathcal{P}(h_1^{(i)}\mid v_1^{(i)})\cdot \mathcal{P}(h_2^{(i)}\mid v_1^{(i)})$结果了，但为什么称它为近似后验呢？很简单，因为$\text{Weak Phase}$过程的那两条红色线是自己假设的，真实模型中是不存在的。
  因此，使用因子分解的方式将$\mathcal{P}(h_1^{(i)},h_2^{(i)}\mid v_1^{(i)})$分解成$\mathcal{P}(h_1^{(i)}\mid v_1^{(i)})\cdot \mathcal{P}(h_2^{(i)}\mid v_1^{(i)})$的形式并分别求解的结果是近似结果，必然会影响精度。但$\text{Weak Phase}$过程并不是追求精度，而是追求效率。这种近似方式所采集的样本仅需要 一次采样过程 即可近似出来，而不是像MCMC要等到平稳分布才可以停止采样。
  虽然‘基于平均场假设变分推断’没有涉及采样，但同样相比不动点方程收敛过程要效率的多。
• $\text{Sleep Phase : }$ 该过程整个是$\text{Sigmoid}$信念网络信息的正常传递过程，这个过程是基于模型产生的。也称生成过程。
  按照这个顺序得到的结果自然是关于‘观测变量后验概率的结果’$\mathcal{P}(v^{\prime }\mid h)$，相当于通过模型生成新的样本，自然是生成过程。
这里的$v^{\prime }$表示从模型中产生的样本结果，这个样本不同于$v$,因为$v$是从真实分布中产生的样本:$v\Rightarrow {\mathcal{P}}_{data}$;而$v^{\prime }$是从模型中产生的样本$v^{\prime }\Rightarrow {\mathcal{P}}_{model}$.
  关于生成模型建模，$\mathcal{P}(v\mid h)$还是$\mathcal{P}(v,h)$均可以。关于联合概率分布$\mathcal{P}(v,h)$建模更加熟悉。如EM算法等：
  $$\log \mathcal{P}(v)=\log \sum _h\mathcal{P}(v,h)$$

$\text{KL Divergence}$观察醒眠算法

这里将$\text{Sleep Phase}$的生成过程(Generative Connection)看作生成模型的步骤，并使用联合概率分布进行建模：
这里的$\theta$指的就是$\text{Sigmoid}$信念网络中表示随机变量结点之间关联关系的模型参数集合$\mathcal{W}$.
例如上图中的$\mathcal{W}$就表示$\left\{{\mathcal{W}}_{h_1^{(i)}\to v_1^{(i)}};{\mathcal{W}}_{h_2^{(i)}\to v_1^{(i)}}\right\}$
$$\text{Generative Model : }\mathcal{P}(v,h;\theta )\theta \Rightarrow \mathcal{W}$$

同理，将$\text{Weak Phase}$的认知过程(Recognization)将其视作模型的形式。通过上面对认知过程的描述，它本质上是对后验概率分布$\mathcal{P}(h\mid v)$的一个近似。这里使用$\mathcal{Q}(h\mid v)$进行表示，并对它进行建模：
同上，符号$\varphi$表示模型$\mathcal{Q}(h\mid v)$的模型参数，也就是上图中反向关联(红色线)的模型参数集合$\mathcal{R}$.
上图中的$\mathcal{R}$则表示$\left\{{\mathcal{R}}_{v_1^{(i)}\to h_1^{(i)}};{\mathcal{R}}_{v_1^{(i)}\to h_2^{(i)}}\right\}$
$$\text{Recognization Model : }\mathcal{Q}(h\mid v;\varphi )\varphi \Rightarrow \mathcal{R}$$

观察醒眠算法是如何学习模型参数的：

• $\text{Weak-Phase : }$

  • $\text{Bottom-up : }$给定真实样本条件下，从隐变量的后验概率分布中进行采样：
    { h ( 1 ) , ⋯   , h ( N ) } ∼ Q ( h ∣ v ; ϕ ) \{h^{(1)},\cdots, h^{(N)}\} \sim \mathcal Q(h \mid v;\phi) {h(1),⋯,h(N)}∼Q(h∣v;ϕ)

  • $\text{Learning Generative Connection : }$基于$\mathcal{Q}(h\mid v;\varphi )$产生的样本，去近似学习生成过程 的参数信息。那么对应的目标函数可表示为：

    1. 就是使用‘蒙特卡洛方法’进行近似。
    2. 添加一个$\log$，不影响最值取值的变化。
    3. 这里$\mathcal{P}(v,h^{(i)};\theta )$中的$v$是真实的训练样本。
    4. 在近似求解模型参数$\theta$的过程中，也就是$\text{Weak Phase}$过程中，关于$\mathcal{Q}(h\mid v;\varphi )$是给定的。即求解$\mathcal{W}$步骤中，$\mathcal{R}$是给定的。初始状态下自然需要一个随机初始化的$\mathcal{R}$.
       $${\mathbb{E}}_{\mathcal{Q}(h\mid v;\varphi )}\left[\log \mathcal{P}(v,h;\theta )\right]\approx \frac{1}{N}\sum _{i=1}^N\log \mathcal{P}(v,h^{(i)};\theta )$$

    那么关于模型参数$\theta$的最优解$\hat{\theta }$可表示为：
    $$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmax}}{\mathbb{E}}_{\mathcal{Q}(h\mid v;\varphi )}\left[\log \mathcal{P}(v,h;\theta )\right]\end{array}$$
    这实际上就是求解 证据下界(Evidence Lower Bound,ELBO) 的最优解：
    $\mathcal{H}\left[\mathcal{Q}(h\mid v;\varphi )\right]$表示近似后验分布$\mathcal{Q}(h\mid v;\varphi )$的熵。
    $$\{\begin{array}{l}\log \mathcal{P}(v)=\text{ELBO}+\text{KL}\left[\mathcal{Q}(h\mid v;\varphi )||\mathcal{P}(v,h;\theta )\right]\\ \begin{array}{rl}\text{ELBO}& =\sum _h\mathcal{Q}(h\mid v;\varphi )\cdot \log \frac{\mathcal{P}(h,v;\theta )}{\mathcal{Q}(h\mid v;\varphi )}\\ & ={\mathbb{E}}_{\mathcal{Q}(h\mid v;\varphi )}\left[\log \frac{\mathcal{P}(h,v;\theta )}{\mathcal{Q}(h\mid v;\varphi )}\right]\\ & ={\mathbb{E}}_{\mathcal{Q}(h\mid v;\varphi )}\left[\log \mathcal{P}(h,v;\theta )\right]+\mathcal{H}\left[\mathcal{Q}(h\mid v;\varphi )\right]\end{array}\end{array}$$
    由于在$\text{Weak Phase}$步骤中$\varphi$是已知参数，因而可以将$\mathcal{H}\left[\mathcal{Q}(h\mid v;\varphi )\right]$看作是一个已知的常量。而求解最值时，常量对最值结果不影响。
    $$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmax}}\text{ELBO}\\ & =\underset{\theta }{\mathrm{argmax}}\left\{{\mathbb{E}}_{\mathcal{Q}(h\mid v;\varphi )}\left[\log \mathcal{P}(h,v;\theta )\right]+\underset{=\mathcal{C}}{\underbrace{\mathcal{H}\left[\mathcal{Q}(h\mid v;\varphi )\right]}}\right\}\\ & =\underset{\theta }{\mathrm{argmax}}\left\{{\mathbb{E}}_{\mathcal{Q}(h\mid v;\varphi )}\left[\log \mathcal{P}(h,v;\theta )\right]\right\}\end{array}$$
    将最初始的期望求解最值问题转化为$\text{ELBO}$求解最值问题，其作用是什么？
    自然是将 求解$\theta$最优解转化为概率分布$\mathcal{Q}(h\mid v;\varphi )$和分布$\mathcal{P}(h,v;\theta )$之间的相关性比较。$\text{ELBO}$最大，意味着$\text{KL}\left[\mathcal{Q}(h\mid v;\varphi )||\mathcal{P}(h\mid v;\theta )\right]$达到最小，此时分布$\mathcal{Q}(h\mid v;\theta )$和分布$\mathcal{P}(h\mid v;\theta )$是最相似的。

• $\text{Sleep Phase : }$
  • $\text{Top-Down}$与$\text{Weak Phase}$步骤相对应，上一步骤求解出的$\hat{\theta }$结果进行固定，并从$\mathcal{P}(h,v;\hat{\theta })$中进行采样：
    此时已经不仅仅采样隐变量了，并且还会采样出‘虚拟的观测变量’。
    { h ( 1 ) , v ′ ( 1 ) , ⋯   , h ( N ) , v ′ ( N ) } ∼ P ( v , h ∣ θ ^ ) \{h^{(1)},v^{'(1)},\cdots,h^{(N)},v^{'(N)}\} \sim \mathcal P(v,h \mid \hat \theta) {h(1),v′(1),⋯,h(N),v′(N)}∼P(v,h∣θ^)
  • 基于$\mathcal{P}(h^{(i)},v^{(i)};\hat{\theta })$中采出的样本，去近似学习认知过程的参数信息。具体目标函数可表示为：
    对应步骤和$\text{Weak Phase}$相似，需要注意$\mathcal{Q}(h^{(i)}\mid v^{{}^{\prime }(i)}\mid ;\varphi )$
    $$\begin{array}{r}{\mathbb{E}}_{\mathcal{P}(h,v;\hat{\theta })}\left[\log \mathcal{Q}(h\mid v;\varphi )\right]\approx \frac{1}{N}\sum _{i=1}^N\log \mathcal{Q}(h^{(i)}\mid v^{{}^{\prime }(i)};\varphi )\end{array}$$
    对应的最优参数$\hat{\varphi }$可表示为：
    $$\hat{\varphi }=\underset{\varphi }{\mathrm{argmax}}\left\{{\mathbb{E}}_{\mathcal{P}(h,v;\hat{\theta })}\left[\log \mathcal{Q}(h\mid v;\varphi )\right]\right\}$$
    观察，上述表达式和$\text{ELBO}$之间是否存在关联关系？对上式进行化简：
    1. 首先将期望展开：
       关于这里确实存在一些个人疑问：为什么不去对$v$进行积分。因为在$\text{Sleep Phase}$中，$v$也是从$\mathcal{P}(h,v;\hat{\theta })$中生成出来的虚拟样本，不同于$\text{Weak Phase}$的真实样本，为什么它可以不用积分？
       $$\hat{\varphi }=\underset{\varphi }{\mathrm{argmax}}\sum _h\mathcal{P}(h,v;\hat{\theta })\log \mathcal{Q}(h\mid v;\varphi )$$
    2. 使用条件概率公式对$\mathcal{P}(h,v;\hat{\theta })$展开，并转换成如下形式：
       分解出的$\mathcal{P}(v;\theta )$明显是不含参数$\varphi$,并且也不含隐变量$h$,将其从积分号中提出来，并视作常数，忽略掉。
       $$\begin{array}{rl}\hat{\varphi }& =\underset{\varphi }{\mathrm{argmax}}\sum _h\mathcal{P}(v;\theta )\cdot \mathcal{P}(h\mid v;\theta )\log \mathcal{Q}(h\mid v;\varphi )\\ & =\underset{\varphi }{\mathrm{argmax}}\left[\mathcal{P}(v;\theta )\cdot \sum _h\mathcal{P}(h\mid v;\theta )\log \mathcal{Q}(h\mid v;\varphi )\right]\\ & =\underset{\varphi }{\mathrm{argmax}}\left[\sum _h\mathcal{P}(h\mid v;\theta )\log \mathcal{Q}(h\mid v;\varphi )\right]\end{array}$$
    3. 在步骤2的基础上，加入一个辅助项$\left[-{\sum }_h\mathcal{P}(h\mid v;\theta )\log \mathcal{P}(h\mid v;\theta )\right]$：
       因为该项中根本不包含任何关于参数$\varphi$的信息，可以将其视作常数，不影响$\varphi$的取值。
这里将符号和$\text{argmax}$合并了~
       $$\begin{array}{rl}\hat{\varphi }& =\underset{\varphi }{\mathrm{argmax}}\left[\sum _h\mathcal{P}(h\mid v;\theta )\log \mathcal{Q}(h\mid v;\varphi )-\sum _h\mathcal{P}(h\mid v;\theta )\log \mathcal{P}(h\mid v;\theta )\right]\\ & =\underset{\varphi }{\mathrm{argmax}}\left[\sum _h\mathcal{P}(h\mid v;\theta )\log \frac{\mathcal{Q}(h\mid v;\varphi )}{\mathcal{P}(h\mid v;\theta )}\right]\\ & =\underset{\varphi }{\mathrm{argmin}}\text{KL}\left[\mathcal{P}(h\mid v;\theta )||\mathcal{Q}(h\mid v;\varphi )\right]\end{array}$$

比对一下$\text{Weak Phase}$和$\text{Sleep Phase}$之间关于模型参数的描述：
$$\{\begin{array}{l}\hat{\theta }=\underset{\theta }{\mathrm{argmin}}\text{KL}\left[\mathcal{Q}(h\mid v;\varphi )||\mathcal{P}(h\mid v;\theta )\right]\\ \hat{\varphi }=\underset{\varphi }{\mathrm{argmin}}\text{KL}\left[\mathcal{P}(h\mid v;\theta )||\mathcal{Q}(h\mid v;\varphi )\right]\end{array}$$
很明显，这两个步骤对于模型参数的优化分别基于不同的$\text{KL Divergence}$。也就是说，这两个参数的更新并没有共用同一个目标函数。
注意$\text{KL Divergence}$中分布顺序与结果之间存在差异。没有什么交换律~

这也是该算法被称为启发式算法的原因，无法确定参数$\varphi ,\theta$是否能够收敛成稳定形式。因而这种方式只能适用于某些模型。

如果将醒眠算法与广义$\text{EM}$算法的迭代思路进行对比的话，发现EM算法无论是E步还是M步，它们均有相同的目标函数——使$\text{ELBO}$达到最大。

但醒眠算法不同。求解$\hat{\theta }$中的$v$是真实样本；而$\hat{\varphi }$中的$v$是模型生成的虚拟样本，实际上在$\text{Sleep Phase}$步骤中，参数更新已经在发生偏移了。
关于$\text{Sleep Phase}$的另一层含义是，不同于$\text{Weak Phase}$以真实样本作为条件，$\text{Sleep Phase}$最初始状态是以入度为零的隐变量结点作为条件。而隐变量就是认人为假定模型中的变量信息。因而都是虚拟样本。
在花书P371页下方也称其为‘幻想粒子’(Fantasy Particle)。在配分函数——随机最大似然中也提到过这个词。

至此，关于$\text{Sigmoid}$信念网络部分介绍到此结束。下一节将介绍深度玻尔兹曼机(Deep Boltzmann Machine,DBM)。

相关参考：
(系列二十六)Sigmoid Belief Network5-醒眠算法-KL Divergence
(系列二十六)Sigmoid Belief Network5-醒眠算法-KL Divergence续