leetcode115.从中序与后序遍历序列构造二叉树，手把手带你构造二叉树（新手向）

构造二叉树是树问题中的难点（相对于遍历二叉树），一开始做的读者会感觉无从下手，这道题在训练营专栏里讲过，是四道题一起讲的，但是现在看来讲的并不全面、具体，所以想单独出一期再来讲一下如何构造二叉树。

这道题给我们中序和后序遍历数组，首先要知道怎么使用它们，后序遍历的特点是左右中的顺序去遍历一棵二叉树，换句话说遍历二叉树总是最后的遍历中间节点，根据这个特性我们可以知道每次要处理的中间节点实际上就在每次递归遍历中的后序数组的最后一个位置上。

举例说明：

先不讲代码，先看中序数组和后序数组如何创建二叉树

inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]

从之前说的我们知道root节点就是3，以3这个节点去切割中序遍历的数组，把中序数组分成左子树和右子树部分，左子树部分是9，右子树部分是15、20、7，删除后序遍历数组最后一个数字，然后进行下一层递归，取后序最后一个数字，20作为中序数组分割条件，这一次把数组分成15和7两部分，至此分割完成。

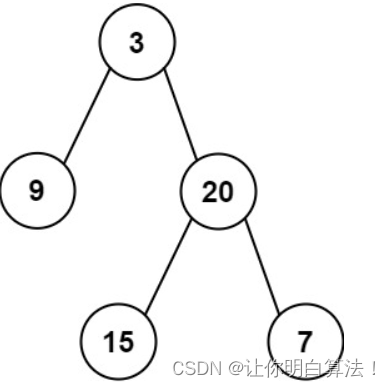
也就是leetcode图中给出的这个示例图。

仔细对照我们说的逻辑，看看能否分成如上图的树，若能理解，请看下面讲解。

写代码之前将代码逻辑讲清楚，代码书写逻辑分为以下七步：

第一步递归判断若后序数组此时无数据，直接返回NULL。

第二步取当前后序遍历数组最后一个数字，并创建一个节点。

第三步判断当前后序遍历数组长度是否为1，若为1说明该节点是叶子节点，不需要向下再递归，直接返回当前节点指针，特别注意，有读者可能觉得这里有些奇怪，第一步是否有些多余？既然节点为叶子节点直接返回，那怎么可能走到数组为空再返回呢？这个我们后面会单独讲解区别。

第四步以当前创建出的节点的值为切割点，在中序遍历数组找到对应切割点位置，并进行切割

第五步切割后序遍历数组

第六步将当前节点左指针对应递归中序遍历数组左子树和后序遍历数组左子树，右指针对应递归中序遍历数组右子树和后序遍历数组右子树。

第七步走到最后说明树创建完成，返回节点。

或许这其中某一步或者某些步看起来有些难以理解，但是我会在之后用代码的形式解释

第一步代码就是简单的判断

if(postorder.size()==0)return NULL;

第二步存储当前后序遍历数组最后一个数字并创建新节点

        int val=postorder[postorder.size()-1];
        TreeNode* node=new TreeNode(val);

第三步判断当前后序数组长度是否为1

if(postorder.size()==1)return node;

第四步——找到切割点位置在中序数组中

        int index=0;
        for(;index<inorder.size();++index){
            if(inorder[index]==val)break;
        }

第四步——切割中序数组

        vector<int>leftinorder(inorder.begin(),inorder.begin()+index);
        vector<int>rightinorder(inorder.begin()+index+1,inorder.end());

第五步切割后序数组（不要忘记先删除最后的一个节点）

    postorder.pop_back();
    vector<int>leftpostorder(postorder.begin(),postorder.begin()+leftinorder.size());
    vector<int>rightpostorder(postorder.begin()+leftinorder.size(),postorder.end());

第六步将当前节点左指针对应递归中序遍历数组左子树和后序遍历数组左子树，右指针对应递归中序遍历数组右子树和后序遍历数组右子树。

        node->left=back(leftinorder,leftpostorder);
        node->right=back(rightinorder,rightpostorder);

第七步返回

        return node;

看完整代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* back(vector<int>& inorder,vector<int>&postorder){
        if(postorder.size()==0)return NULL;
        int val=postorder[postorder.size()-1];
        TreeNode* node=new TreeNode(val);
        if(postorder.size()==1)return node;
        int index=0;
        for(;index<inorder.size();++index){
            if(inorder[index]==val)break;
        }
        vector<int>leftinorder(inorder.begin(),inorder.begin()+index);
        vector<int>rightinorder(inorder.begin()+index+1,inorder.end());
        postorder.pop_back();
    vector<int>leftpostorder(postorder.begin(),postorder.begin()+leftinorder.size());
    vector<int>rightpostorder(postorder.begin()+leftinorder.size(),postorder.end());
        node->left=back(leftinorder,leftpostorder);
        node->right=back(rightinorder,rightpostorder);
        return node;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return back(inorder,postorder);   
    }
};

怎么样是不是特别清晰了，有注意到写代码时候有几步被特别标记在块引用里吗？这是代码中的重点部分。

现在由我来解答读者可能遇到的各种问题。.

问题1：为什么要先进行中序遍历数组的分割而不是后序的分割？

这个中序遍历数组分割我加粗很多次了，读者们应该都注意到了，这是为什么？实际上只能先进行中序数组分割，因为我们只能靠后序遍历数组来确定中间节点填写什么，中序数组无法确定节点，而后序数组无法确定左右子树分割，因为后序数组左右子树是挨在一起的，它没有分界点，这都是由于中序和后序的遍历顺序决定的，中序为左中右，后序为左右中，这也就是为什么中序能被中节点所分割的原因，而找中节点为什么要用后序数组的原因。

有一道很相似的题目是给你前序和中序遍历数组，让你构造一棵树，也是同样的道理，前序遍历由于先遍历中节点所以第一个位置的前序遍历数据就是中节点，拿这个数据去分割中序遍历数组就可以了，前序数组和后序数组不能构造二叉树，因为两种遍历方法均只能确定中节点，它们任何一个都无法对左右子树做分割，这是其中一个原因，另一个原因在于前后序遍历无法唯一确定一棵二叉树，这是最重要的原因。

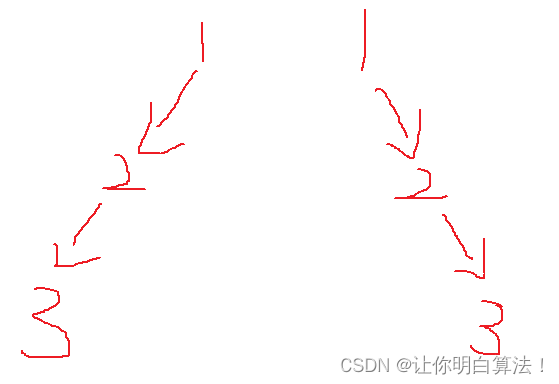
我上面画的图它们是两颗完全不同的树，但是其前后序遍历数组内容是一样的。

问题2：我们上面说了后序遍历数组的左右子树部分数据是挨在一起的，不能用中节点分割，那我们是如何实现后序遍历数组的分割的？

这个和先分割的中序数组有关，我们用中序数组的左子树大小来分后序数组的左子树大小，中序数组的右子树大小来分后序数组的右子树大小，因为左右子树无论是怎么遍历节点数量肯定是不发生改变的，而中序遍历切割就是拿后序数组的数据切割的，所以中序的切割左右子树大小理应对应着后序遍历数组的左右子树大小，但是要注意中序左右子树的大小和后序左右子树大小相等，但是并不意味着其中左右子树的节点顺序也一定保持相同，因为两种遍历顺序的差异，根本不可能相同。还拿这个测试用例

inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]

读者自行举例便知结论的正确与否。

问题3：为什么切割中序遍历时右子树其实部分要用左子树的末尾下标+1？根据cpp的原理来看使用迭代器做这种结尾通常是不被包含的，那为什么右子树开始还要进行+1，这不会导致有一个节点被落下吗？

不要忘记我们为什么后序遍历数组要进行最后一个数据的删除，因为该中间节点已经被创建并加入了树的构建，所以一定不要使节点在下一次递归时重复出现。

问题4：步骤1和步骤3的思想是否发生重复？

这个是不重复的，而且没有步骤1会发生异常终止，但是没有步骤3没有问题，步骤3只是为了剪枝。遇到叶子节点就会向上返回所以不需要判断后序数组长度是否为0是错误的想法，该测试用例中使用中序【2，1】后序【2，1】的测试用例。
第一次递归分中后序数组的左右部分之后，后序数组由于减少一个元素的缘故，后序数组的右部分子树数组并没有数据，所以没有了第一个if判断，递归下去时候，会对一个无数据的数组取数，导致异常退出。整个过程中第二个if也就是叶子节点处返回都还没有进行，就导致异常终止了。
可见叶子节点及时返回这个终止逻辑并不能阻止此类bug的发生。

应该没有什么其他的问题了，如果读者有请在评论区留言给我。

使用vector在函数内部，每一次递归都需要开辟，为了节省空间和提高运行效率也可以用传入下标的方法来实现对递归时左右子树的控制，详情见下面代码。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* back(vector<int>&inorder,int inbegin,int inend,vector<int>&postorder,int pobegin,int poend){
        if(pobegin==poend)return NULL;
        int val=postorder[poend-1];
        TreeNode* root=new TreeNode(val);
        if(poend-pobegin==1)return root;
        int index;
        for(index=inbegin;index<inend;++index){
            if(inorder[index]==val)break;
        }
        int leftinorderbegin=inbegin,leftinorderend=index;
        int rightinorderbegin=index+1,rightinorderend=inend;
        int leftpostorderbegin=pobegin,leftpostorderend=pobegin+index-inbegin;
        int rightpostorderbegin=leftpostorderend;
        int rightpostorderend=poend-1;
        root->left=back(inorder,leftinorderbegin,leftinorderend,postorder,leftpostorderbegin,leftpostorderend);
        root->right=back(inorder,rightinorderbegin,rightinorderend,postorder,rightpostorderbegin,rightpostorderend);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return back(inorder,0,inorder.size(),postorder,0,postorder.size());
    }
};

代码思路和前面的代码思路一模一样，只是我们采用了下标传入的方法，核心思想是不变的，大家可以对照前次代码类比一下。

本期内容就到这里
如果对您有用的话别忘了一键三连哦，如果是互粉回访我也会做的！

大家有什么想看的题解，或者想看的算法专栏、数据结构专栏，可以去看看往期的文章，有想看的新题目或者专栏也可以评论区写出来，讨论一番，本账号将持续更新。
期待您的关注