1.回溯是什么?
- 回溯,也叫回溯搜索法,搜索的一种方式。
- 回溯搜索实际上也是一种暴力搜索(本质是穷举)(对于有些问题是唯一可以解决的办法了,for循环是不适用的)
- 和别的搜索不同之处在于它能处理的数据可以抽象成树结构。
回溯和递归的区别:
递归是个方法的话,回溯是其中的一个操作。
回溯方法实际上也是递归方法。回溯是递归的伴生品。
补充:
递归和迭代的区别是迭代通过自定义栈模拟递归的。
2.回溯用来解决哪些问题?
图摘自《代码随想录》
总结:
组合问题|排列问题: 组合不强调顺序,排列强调顺序
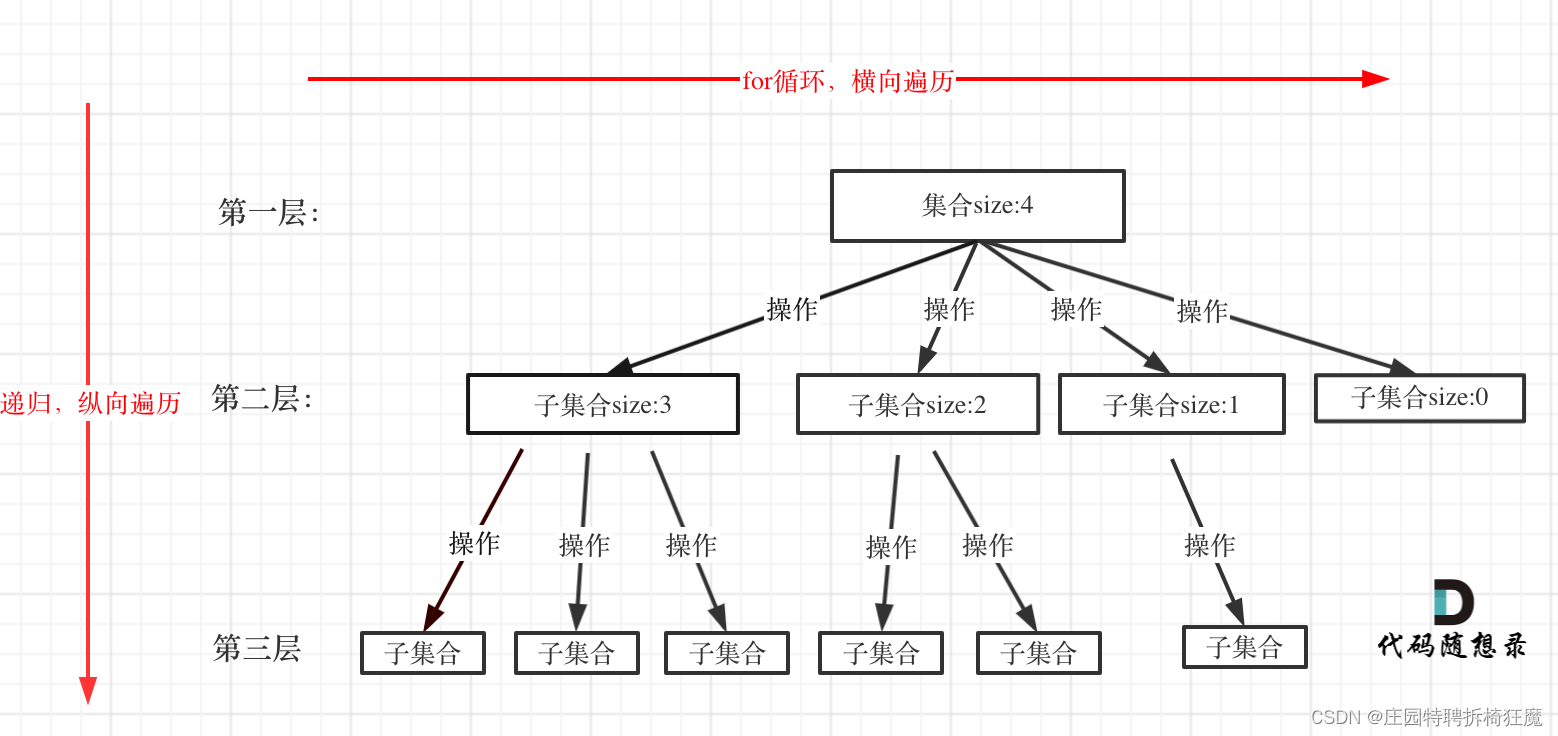
如何抽象成树结构:(前提:回溯都是在集合中找满足条件的子集)
1.集合的大小:树的宽度
2.递归的深度:树的深度
3.满足条件的结果:叶子节点
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
图摘自《代码随想录》
3.回溯解题模板
1.确定返回值及参数
一般返回值void
一般名称为backtracking
一般参数列表比较复杂,可能需要一边梳理思路,一边添加。
2.确定终止条件
在叶子节点收集满足条件的结果
搜索的结果总是根节点到叶子节点的路径,可以使用数组来保存。
3.回溯搜索遍历过程:
一般是一个for循环,遍历当前分支
用来撤销当前操作,向上一层返回
【建议熟记版】
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}