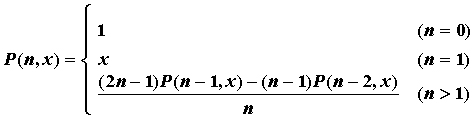分类问题的评估是看实际类别和预测类别是否一致，它的评估指标主要有混淆矩阵、AUC、KS。回归问题的评估是看实际值和预测值是否一致，它的评估指标包括MAE、MSE、RMSE、R方。

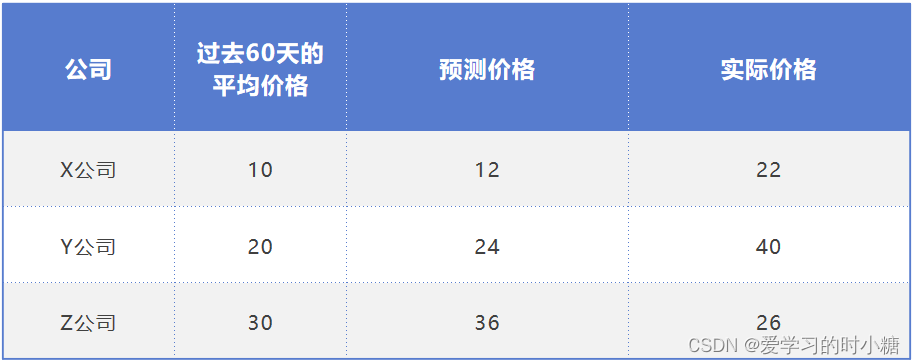
如果我们预测第二天某支股票的价格，给一个模型 y=1.5x，x是最近60天股票的价格的平均值，y是预测的第二天股票的结果。我们选择三支股票，记录它过去60天的均价，以及模型预测出来的价格和实际的价格。

下面的图片是将过去60天股票均价作为X轴，将股票价格作为Y轴做出的散点图。

我们想要算出预测和实际结果的差异，最原本的方法是直接将每一个样本的预测值和实际值做差，再将所有的差值结果进行相加。

它们的差值情况分别为：22-12=10，40-24=16，26-36=-10。可以看到Z公司的差值为-10，它与其他的差值相加会造成抵消误差的情况，所以这种方法不合理。

为了避免差值相互抵消的情况，我们将差值的平方相加。

这种计算误差的方式在会受到样本个数的影响，在样本比较少的情况下它的误差会比较小，样本比较多的话，误差会较大。为了避免这种情况的出现，我们将平方和计算出来的误差除以样本个数就可以不受样本个数的影响，这种计算误差的方式我们称为均方误差。

一、MSE（均方误差）

其中n：样本数量  :表示实际值 :表示预测值

计算方式就是：样本的实际值和样本预测值差值的平方再除以样本数量。

这个值一定是大于等于0的，我们在评估的时候应该让这个值越小越好。

二、RMSE（均方根误差）

在使用均方误差对于值取平方的时候，会导致量纲发生变化，比如：我们计算的是米，但是平方之后是平方米，为了保持量纲一致，我们再对它开方，也就是均方根误差。

这个数值结果也是越小越好的。 

三、MAE（绝对平均值）

我们将差值取平方的原因是为了避免正负抵消操作，我们还可以使用差值取绝对值的方式来避免抵消，计算误差。

这个数值结果也是越小越好。 

四、R方

在模型预测过程中，我们可能会想用同一个模型解决不同得问题。由于预测样本不一致，最终的预测结果可能会随着量纲的差异上至几万，下至几百。为了避免这种情况的出现，将误差使用0-1的概率表示出来，我们使用R方的计算公式。

是实际结果和预测值之间相关系数的平方。

TSS：表示总离差平方和。就是实际值和实际值均值的差值平方和。

RSS：表示残差平方和。实际值和预测值之间的差值平方和。

它的值一般在0-1的范围内，越靠近1，说明模型预测的越准确。 

我们继续使用上面股票预测的例子来说明这个R方的计算方法。

第一步：求实际值均值： 

第二步： 

第三步： 

第四步：带入公式， 

五、误差公式选择

均方误差会进行差值平方，有一个数据放大的过程。均方根误差虽然平方再开方，但是还是会比实际的误差大，所以我们一般想要更接近误差的数据，选择MAE。

对于算法工程师而言，将误差放大有利于他们发现误差。算法工程师一般会选择MSE和RMSE。

六、总结

1.想获得更加真实的误差结果选择MAE，想要找到更明确的误差选择MSE。

2.如果想要将一个模型应用解决不同的问题时，选择可以看到模型在那个问题上表现得更好。

参考文献：刘海丰——《成为AI产品经理》 自用，请勿传播