Splay树和AVL树是两种不同的自平衡二叉搜索树实现。
1. 平衡条件:AVL树通过维护每个节点的平衡因子(左子树高度减去右子树高度)来保持平衡,要求每个节点的平衡因子的绝对值不超过1。Splay树则通过经过每次操作后将最近访问的节点调整到根节点的方式来保持平衡,而不依赖于平衡因子。
2. 平衡调整:AVL树在进行插入或删除操作时,可能需要通过旋转来调整树的结构以保持平衡。旋转的过程比较固定,需要进行左旋、右旋、双旋等操作。Splay树在进行操作时,将最近访问的节点通过一系列旋转操作调整到根节点,称为"伸展"操作。这种伸展操作将最近访问的节点置于更接近根节点的位置,从而实现了平衡。
3. 时间复杂度:AVL树保证了每个节点的左右子树高度差不超过1,因此可以保证所有操作的时间复杂度为O(logN),其中N是树的节点数量。Splay树的操作时间复杂度是均摊的,具体取决于节点的访问模式。对于频繁访问的节点,其操作时间复杂度可能接近O(1),但对于其他节点,可能会有较高的时间复杂度。
4. 动态性能:AVL树在插入、删除和查找操作的平均和最坏情况下都具有较好的性能,但可能会频繁地进行旋转操作。相比之下,Splay树对于最近访问的节点有更好的动态性能,因为它将这些节点调整到根节点位置,使得下一次访问更快。然而,对于没有被频繁访问的节点,Splay树的性能可能较差。
综上所述,AVL树和Splay树在平衡调整的策略、时间复杂度和动态性能方面有所不同。AVL树适用于对平衡性要求较高、操作频率较低的场景,而Splay树则适用于需要频繁访问最近访问节点的场景。
树旋转
void rotate(int &cur,int f) {
int son = TR[cur].ch[f];
TR[cur].ch[f] = TR[son].ch[f ^ 1];
TR[son].ch[f ^ 1] = cur;
cur = son;
}
f表示cur结点的对应孩子,多一个son指针指向它;cur指向的是要旋转的结点,是被旋转下去的结点,son是被旋转上来的结点;即cur为原根节点,son为新根结点。但是cur,始终指向根节点位置,也就是树的根节点编号
原根结点与新根结点满足f关系,则新根结点之前的所有孩子也和原根结点满足f关系;旋转后,则原根结点与新根结点满足f^1关系,要让原根结点的f位置处更新,也要使其满足与原根节点的f关系,但是要和新根结点满足f^1关系,则只能选择新根结点的f^1处的孩子,接到原根节点f处。
旋转步骤:
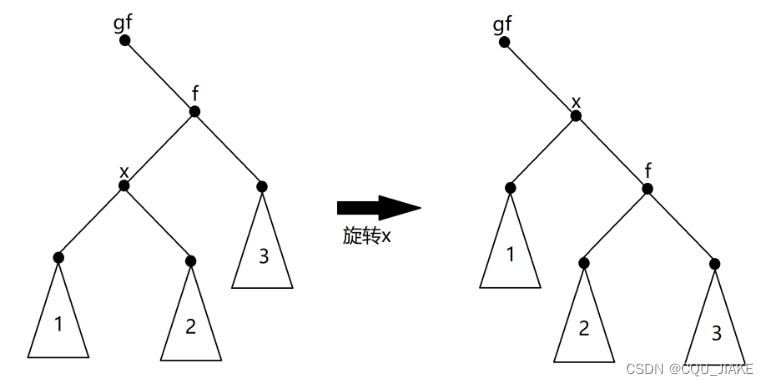

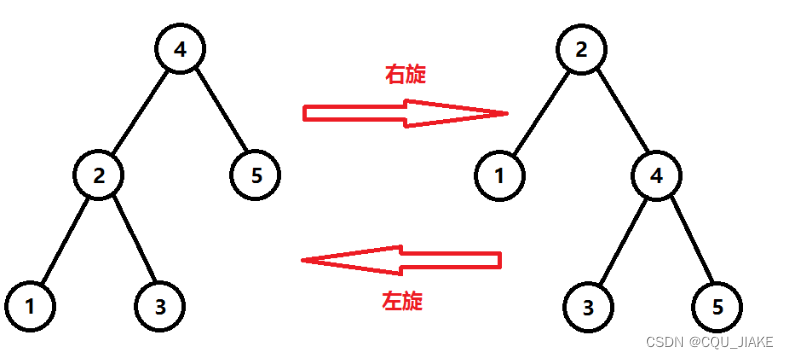


void rotate(int x)
{
int y=t[x].fa,z=t[y].fa,chk=get(x);
t[y].ch[chk]=t[x].ch[chk^1];//1
if(t[x].ch[chk^1])
t[t[x].ch[chk^1]].fa=y;//2
t[x].ch[chk^1]=y;//3
t[y].fa=x;//4
t[x].fa=z;//5
if(z)
t[z].ch[y==t[z].ch[1]]=x;//6
maintain(y);
maintain(x);
}
旋转后的性质
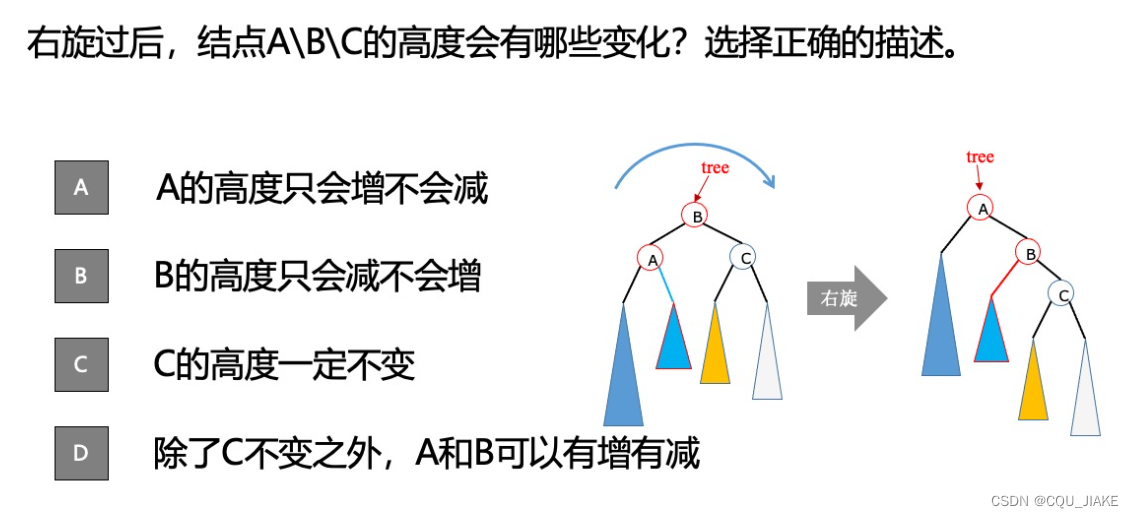
ABC。
进行右旋后,右子树得到一个原根节点为一层,并且原根节点得到新根结点原右子树,故左子树高度至少增加一层;同样,左旋后,左子树的高度至少增加1
旋转时机
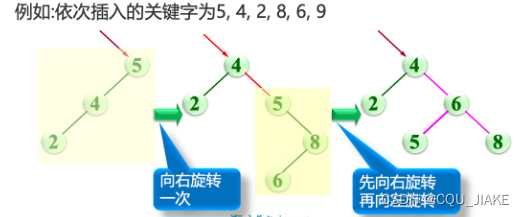
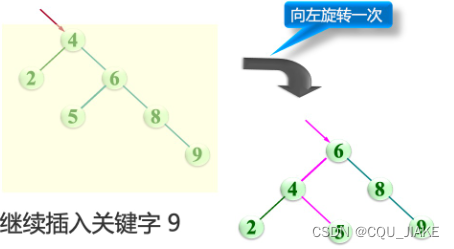
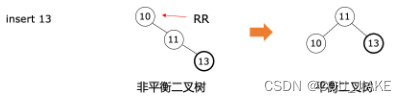

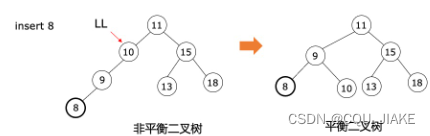
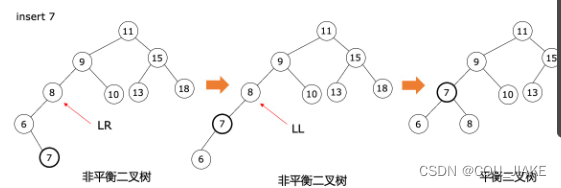
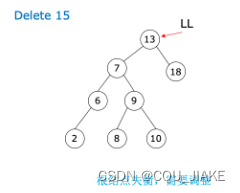
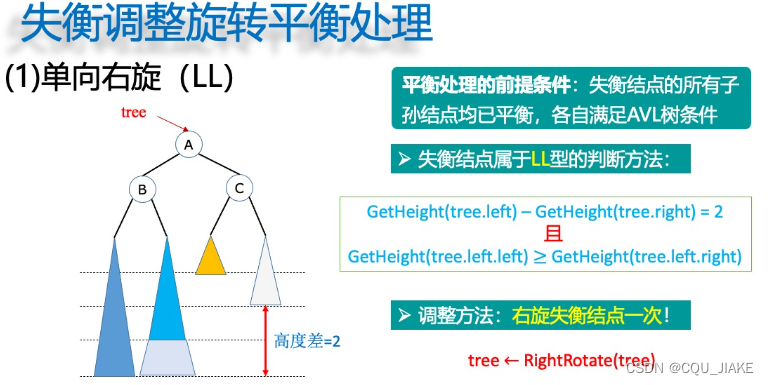
要进行左旋,说明右子树重;要进行右旋,说明左子树重。
这种重代表高度的失衡,表达为

即此时就一定需要旋转了。
接着判断重的子树的左子树与右子树高度关系
如果重的方向连续一样,那就做反方向一次调整;不然,就做一次调整,使之变为对应情况,再进行反方向一次调整
如果左子树的左子树高度比左子树的右子树高度大,就说明是一直左边很大,往右允(右旋)一下就行
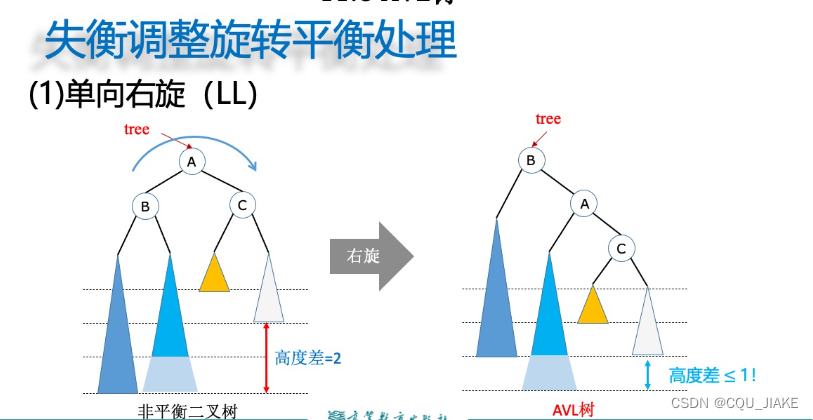

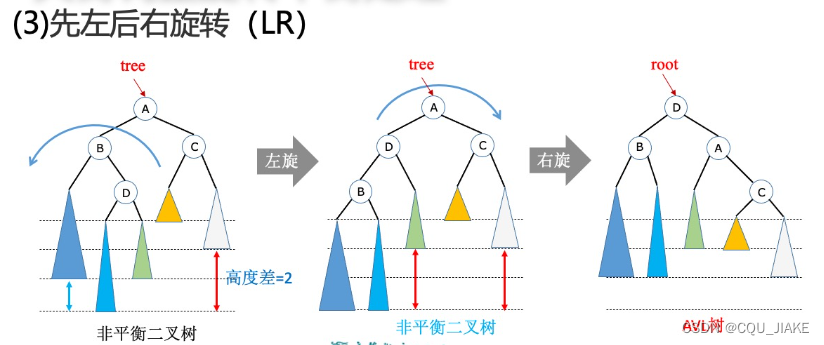

 就是旋转前有个判断,如果LL,RR就旋一次就行;不然就先旋一次构成LL,RR再进行一次旋
就是旋转前有个判断,如果LL,RR就旋一次就行;不然就先旋一次构成LL,RR再进行一次旋
所谓三点共线,就是父亲和儿子的类型相同,即都是左孩子或都是右孩子,不能一左一右
操作
旋转
void rotate(int x)
{
int y=t[x].fa,z=t[y].fa,chk=get(x);
t[y].ch[chk]=t[x].ch[chk^1];//1
if(t[x].ch[chk^1])
t[t[x].ch[chk^1]].fa=y;//2
t[x].ch[chk^1]=y;//3
t[y].fa=x;//4
t[x].fa=z;//5
if(z)
t[z].ch[y==t[z].ch[1]]=x;//6
maintain(y);
maintain(x);
}
x表示被旋上去的结点,是新根结点,识别x是原根结点的什么孩子,做相应的旋转
具体是左旋还是右旋取决于 chk 的值,如果 chk 为0,则进行右旋操作;如果 chk 为1,则进行左旋操作。
SPLAY
将根节点旋转到根

void splay(int x)
{
for(int f=t[x].fa;f=t[x].fa,f;rotate(x))
if(t[f].fa)
rotate(get(x)==get(f)?f:x);
root=x;
}
子树大小


对于节点3来说,它的左子节点是2,右子节点是4。节点的重复次数为2,表示节点上存储的值3重复出现了两次。
对于节点2来说,它的左子节点为空,右子节点为空。节点的重复次数为1。
对于节点4来说,它的左子节点为空,右子节点是5。节点的重复次数为3,表示节点上存储的值4重复出现了三次。
对于节点5来说,它的左子节点为空,右子节点为空。节点的重复次数为2。
现在我们来计算节点的子树大小 sz。
对于节点3来说,它的 sz 值应该等于左子树的 sz 值加上右子树的 sz 值,再加上节点自身的重复次数。左子树为空,右子树只有一个节点4,所以左子树的 sz 值为0,右子树的 sz 值为4。节点3的重复次数为2。因此,节点3的 sz 值为0 + 4 + 2 = 6。
同样的道理,对于节点2来说,它的 sz 值为左子树的 sz 值加上右子树的 sz 值,再加上节点自身的重复次数。左子树为空,右子树为空,节点2的重复次数为1。因此,节点2的 sz 值为0 + 0 + 1 = 1。
以此类推,可以计算出其他节点的 sz 值。
这个就是考虑到树中存储元素会有重复的,考虑到了重复的情况,就加了一个重复权值,即sz,sz越大,这个结点展开后的序列就越长,但是存储时就是一个值的结点
插入

旋转:将当前节点旋转到根
void insert(int k)
{
if(!root)//若树为空
{
t[++tot].val=k;
t[tot].cnt++;
root=tot;
maintain(root);
return;
}
int cur=root,f=0;
while(1)
{
if(t[cur].val==k)//1
{
t[cur].cnt++;
maintain(cur);
maintain(f);
splay(cur);
break;
}
f=cur;
cur=t[f].ch[t[f].val<k];//2
if(!cur)//3
{
t[++tot].val=k;
t[tot].cnt++;
t[tot].fa=f;
t[f].ch[t[f].val<k]=tot;
maintain(tot);
maintain(f);
splay(tot);
break;
}
}
}
1. 首先检查树是否为空。如果树为空,则创建一个新节点,将其值设置为 `k`,重复次数 `cnt` 设置为1,并将其作为根节点。然后调用 `maintain` 函数维护根节点的信息,并返回。
2. 如果树不为空,则通过循环找到插入位置。初始化 `cur` 为根节点的索引,`f` 为当前节点的父节点的索引。
3. 在循环中,首先检查当前节点 `cur` 的值是否等于待插入的值 `k`。如果相等,则更新当前节点的重复次数 `cnt`,调用 `maintain` 函数维护当前节点和其父节点的信息,然后调用 `splay` 函数将当前节点旋转到根节点位置。这是为了保持伸展树的特性,即插入的节点被旋转到根节点位置。
4. 如果当前节点的值不等于待插入的值 `k`,则更新 `f` 为当前节点 `cur`,并根据 `k` 的大小决定往左子树还是右子树方向移动。即,如果 `k` 小于当前节点的值,则将 `cur` 更新为当前节点的左子节点索引;如果 `k` 大于当前节点的值,则将 `cur` 更新为当前节点的右子节点索引。
5. 如果当前节点 `cur` 为空(达到了叶子节点),则说明待插入的值不在树中,需要创建一个新节点,将其值设置为 `k`,重复次数 `cnt` 设置为1,并将其插入到当前节点 `f` 的对应子节点位置。然后调用 `maintain` 函数维护新插入节点和其父节点的信息,再调用 `splay` 函数将新插入节点旋转到根节点位置。
通过这些操作,可以将新的节点插入到伸展树中,并将其旋转到根节点位置,以维持树的平衡性和性能。
查询排名,根据元素返回排名

每沿着树往下走一次,就意味着左右子树所能容纳的元素数量就会少一个等级,即深度增加一次,而不是类似于区间一样容纳从开始到这里的所有元素,而只是和上个根节点一同构成的一个区间里的所有元素。所以在x大于当前结点时,也要加上当前结点的所有左子树大小,因为下一步是要往这个结点的右子树上走,走了之后深度加一,区间左端点就不再包括上个根节点的左子树,区间左端点就是上个根节点(因为上个根节点的所有右子树上元素都比根节点大)
int rnk(int x)
{
int res=0,cur=root;
while(1)
{
if(x<t[cur].val)//向左子树走,而不用累加答案,因为比x小的都在左子树
cur=t[cur].ch[0];
else
{
res+=t[t[cur].ch[0]].size;//累加左子树的size,因为左子树上的权值都小于x
if(x==t[cur].val)//如果权值与x相等
{
splay(cur);//旋转
return res+1;//“排名定义为比当前数小的数的个数+1”
}
res+=t[cur].cnt;//累加当前节点size,因为当前节点权值小于x
cur=t[cur].ch[1];//右子树
}
}
}
查询数值,根据排名返回元素

之所以要减去左子树size以及当前结点cnt,是因为每个结点记录的都只是大小,子树的大小,自身的权值,而不是记录整体的一个排名
k<=0时说明已经找到,就是当前这个结点。=0时说明刚好找到,<0则说明当前这个结点有重复的,如1,1,1,1,查询到的是第2个或第3个1
int kth(int k)
{
int cur=root;
while(1)
{
if(t[cur].ch[0]&&k<=t[t[cur].ch[0]].size)//左子树存在且排名为k的值在左子树
cur=t[cur].ch[0];
else
{
k-=t[t[cur].ch[0]].size+t[cur].cnt;//将k改为在右子树的排名
if(k<=0)//如果排名小于等于0,说明已经找到,直接返回
{
splay(cur);
return t[cur].val;
}
cur=t[cur].ch[1];
}
}
}
前驱与后继
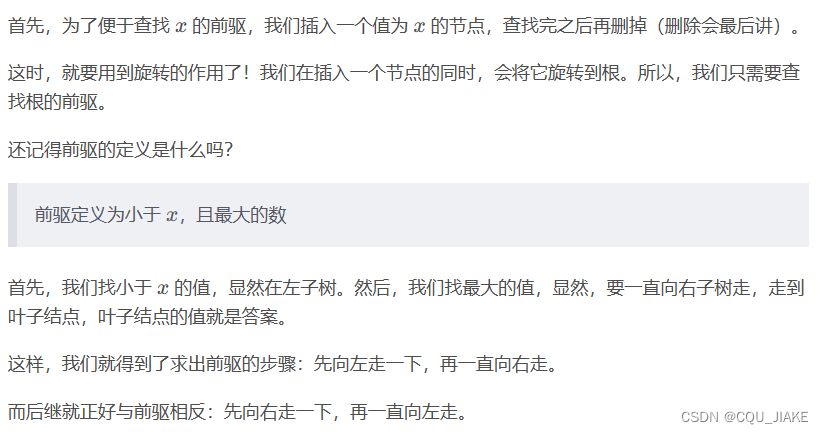
int pre()
{
int cur=t[root].ch[0];//向左
if(!cur)//如果已经到叶子结点
return cur;
while(t[cur].ch[1])//向右
cur=t[cur].ch[1];
splay(cur);//旋转
return cur;
}
int nxt()
{
int cur=t[root].ch[1];//向右
if(!cur)
return cur;
while(t[cur].ch[0])//向左
cur=t[cur].ch[0];
splay(cur);//旋转
return cur;
}
删除

先调用rnk(k)来定位值为K的结点,并将其调整到根节点
void del(int k)
{
rnk(k);
if(t[root].cnt>1)//1
{
t[root].cnt--;
maintain(root);
return;
}
if(!t[root].ch[0]&&!t[root].ch[1])//2
{
clear(root);
root=0;
return;
}
if(!t[root].ch[0])//3
{
int cur=root;
root=t[root].ch[1];
t[root].fa=0;
clear(cur);
return;
}
if(!t[root].ch[1])//4
{
int cur=root;
root=t[root].ch[0];
t[root].fa=0;
clear(cur);
return;
}
int cur=root;//5
int x=pre();
t[t[cur].ch[1]].fa=root;
t[root].ch[1]=t[cur].ch[1];
clear(cur);
maintain(root);
}
需要注意,pre之后,x就成为了新根结点,通过cur保留一个指针指向原根节点。
原根节点的先序一定在左子树上,所以变为新根结点时一定是右旋,而且原根节点的先序一定是叶子结点,一定没有孩子,所以可以直接接。或者,先序成为新根结点后,其右子树一定一定是原根节点,因为是其先序,右子树比根大。
让原根节点的右孩子的父亲更新为新根结点,让新根结点的右孩子更新为原根节点的右孩子